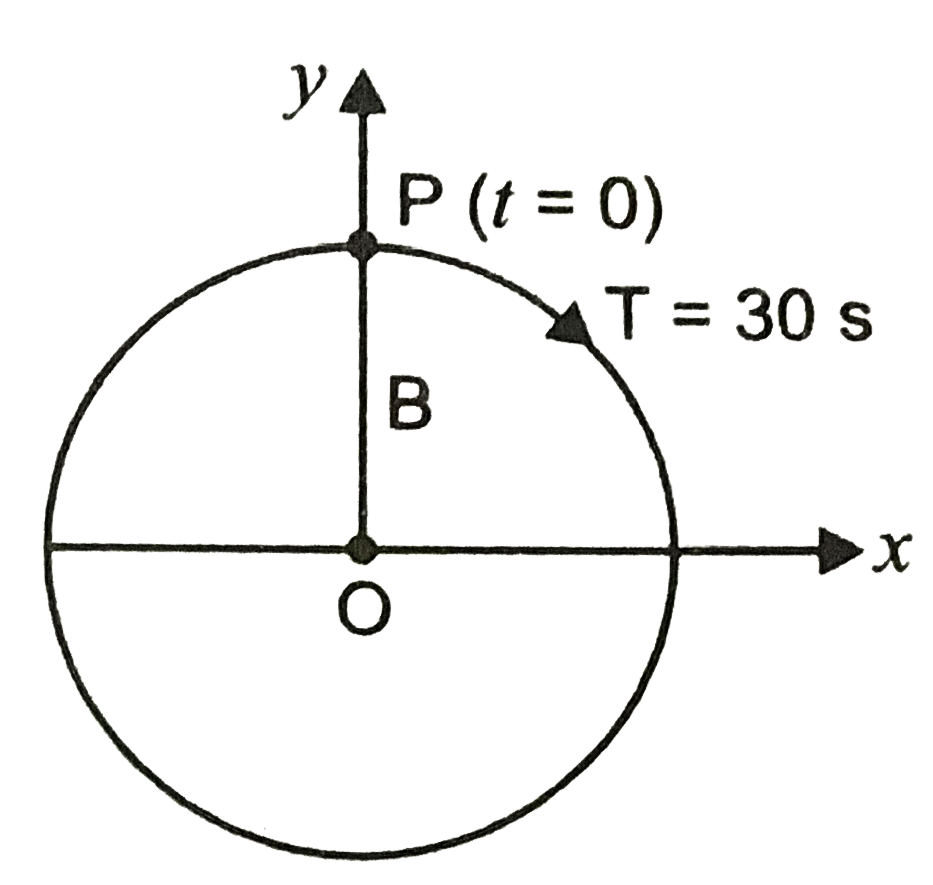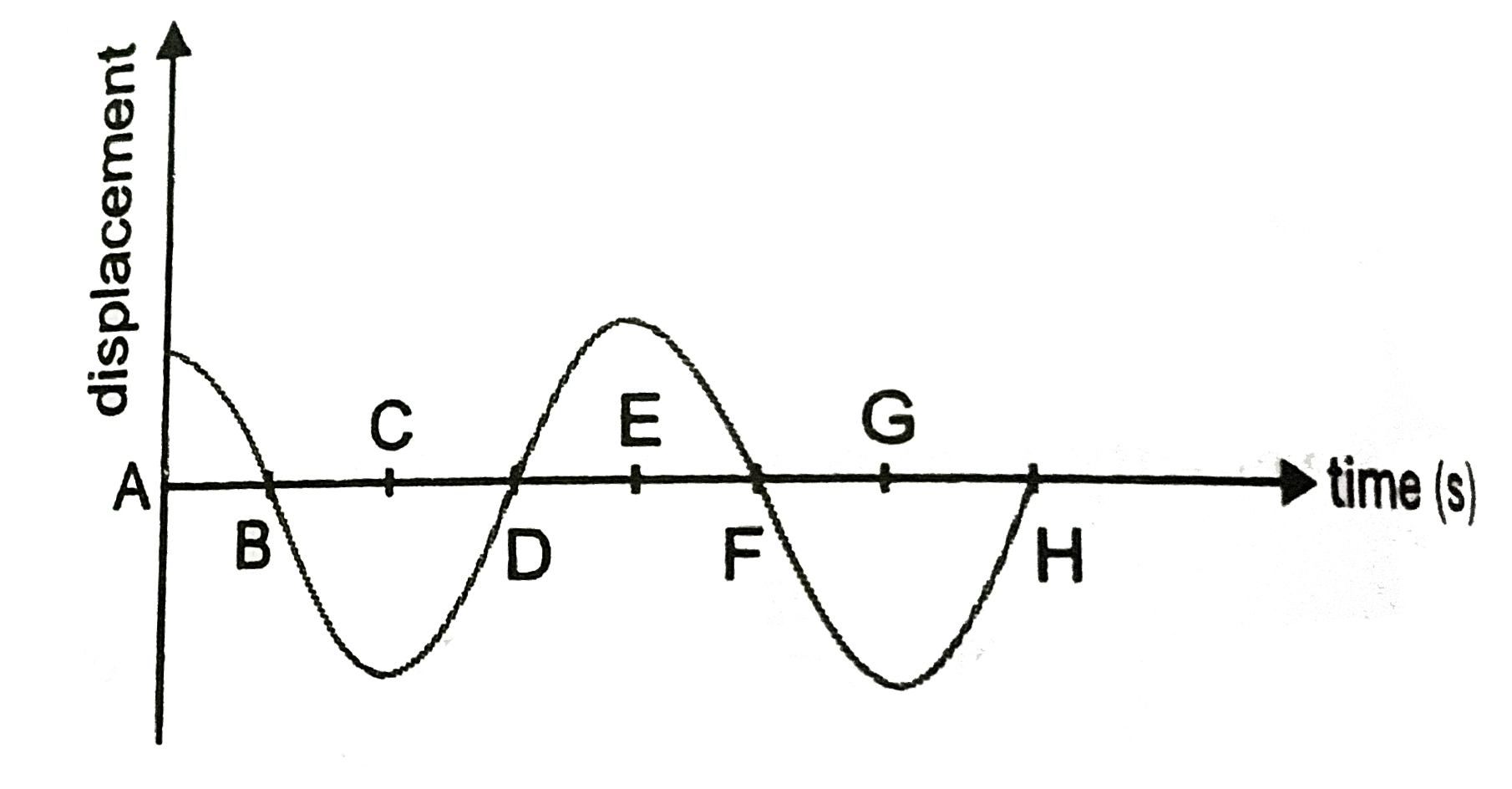NCERT Exemplar Problems Subjective Question (Very short Answer Type Questions ) from MODERN PUBLISHERS PHYSICS (HINGLISH) OSCILLATIONS for Class 11
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| MODERN PUBLISHERS PHYSICS (HINGLISH) | NCERT Exemplar Problems Subjective Question (Very short Answer Type Questions ) |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
Which of the following examples represent periodic motion?
(a) A swimmer completing one return trip from one bank of a river to other bank. (b) A freely suspended bar magnet displaced from its N−S direction and released. (c) A hydrogen molecule rotating about its centre of mass. (d) An arrow released from a bow. View SolutionQuestion 2
Which of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
(a) The rotation of earth about its axis. (b) Motion of an oscillating mercury column in a U tube,
(c) Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower most position. (d) General vibrations of a polyatomic molecule about its equilibrium position. View SolutionQuestion 4
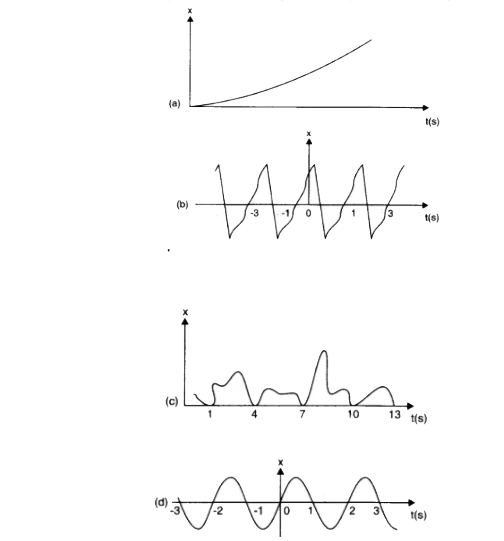
Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic , and (c) non-periodic motion ? Give period for each case of periodic motion ,ω is any positive constant). (a) sinωt−cosωt) (b) sin3ωt (c) 3cos(π4−2ωt)
(d) cosωt+cos3ωt+cos5ωt) (e) exp(−ω2t2) (f) 1+ωt+ω2t2 View SolutionQuestion 5
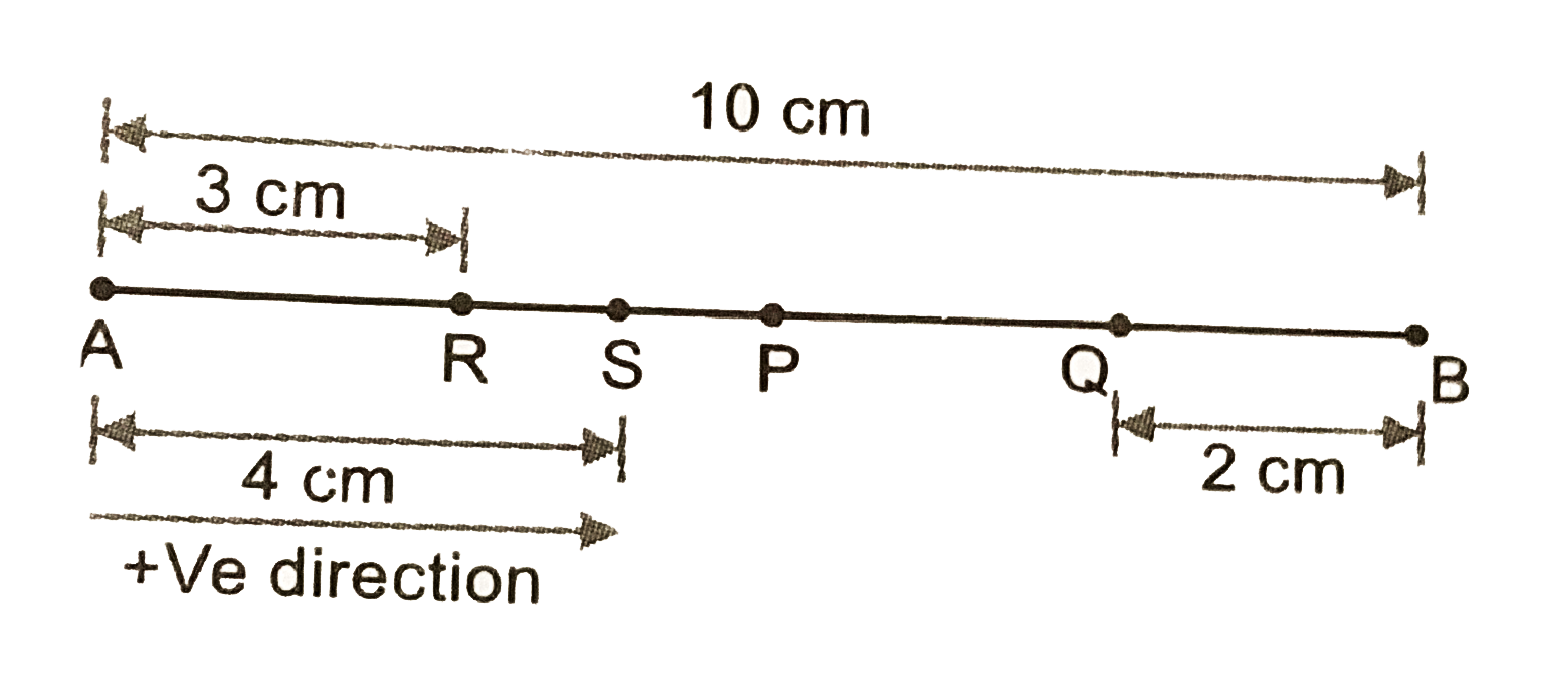
A particle is in linear S.H.M. between two points A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is.
(a) at the end A (b) at the end B,
(c) at the mid point of AB going towards A,
(d) at 2 cm away from B going towards A,
(e) at 3 cm away from A goiing towards B, and
(f) at 4 cm away from A going towards A.
 View Solution
View SolutionQuestion 7
The motion of a particle in S.H.M. is described by the displacement function, x=Acos(ωt+ϕ), If the initial (t=0) position of the particle is 1cm and its initial velocity is ωcms−1, what are its amplitude and initial phase angle ? The angular frequency of the particle is πs−1. If instead of the cosine function, we choose the sine function to describe the SHM:x=Bsin(ωt+α), what are the amplitude and initial phase of the particle with the above initial conditions ?View SolutionQuestion 9
A spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.
 View Solution
View SolutionQuestion 10
In exercise 14.9 let us take the position of mass when the spring is unstretched as x = 0, and the direction from left to right as the positive direction of X-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is
(a) at the mean position.
(b) at the maximum stretched position, and
( c ) at the maximum compressed position.
IN what way do these functions for SHM differ from each other, in frequency in amplitude or the initial phase ? View SolutionQuestion 11
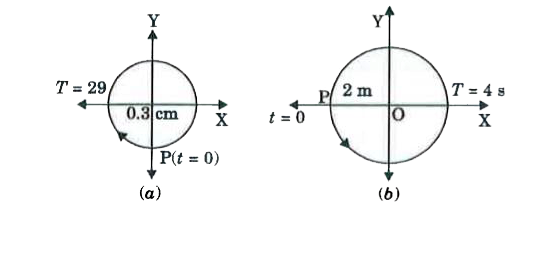
Figure below correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anticlockwise) are indicated on each figure. Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P in each case.
 View Solution
View SolutionQuestion 12
Plot the corresponding reference circle for each of the following simple hoarmonic motions. Indicate the intial(t=0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case :(x is in cm and t is in s ).
(a) x=−2sin(3t+π/3) (b)x=cos(π/6−t) (c) x=3sin(2πt+π/4) (d) x=2cosπtView SolutionQuestion 13
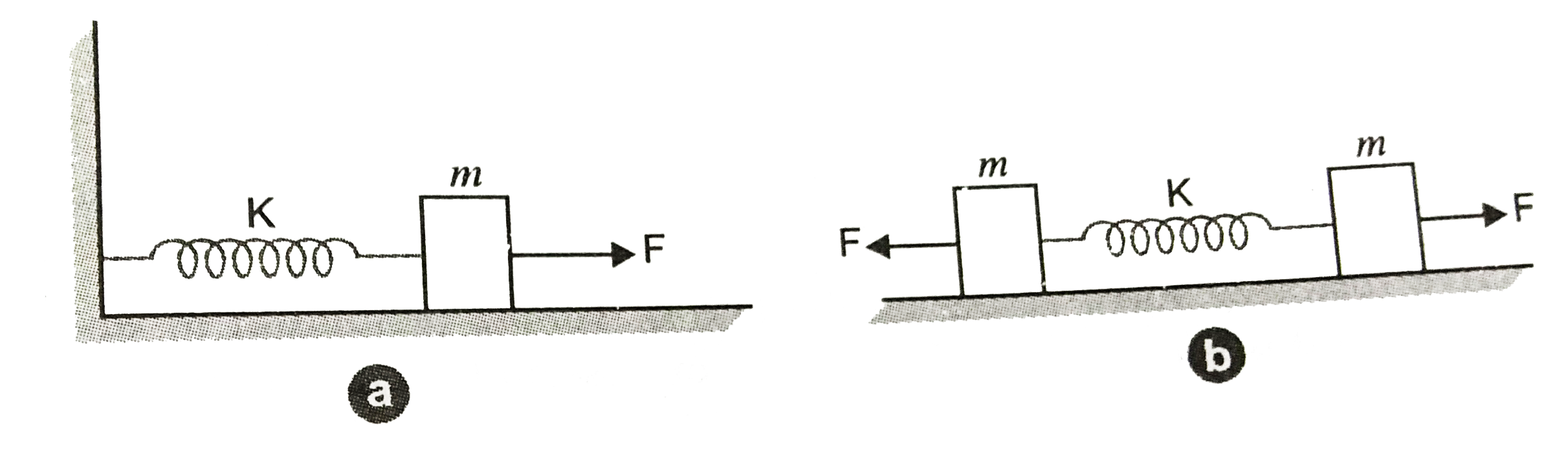
Figure a) shows a spring of force constant k clamped rigidly at once end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?
 View Solution
View SolutionQuestion 16
Answer the following questions: (a) Time period of particle is S.H.M. depends on the force constant k and mass m of the particle :T=2π√m/k. A simple pendulum executes S.H.M. approximately. Why then is the time-period of a pendulum independent of the mass of the pendulum?
(b) The motion of simple pendulum is approximately simple harmonic for small angles of oscillation. For large angle of oscillation, a more involved analysis (beyond the scope of this book) shows that T is greater that 2π√l/g. Think of a quantitative argument to appreciate this result.
(c) A man with a wrist watch on his hand falls from the top of tower. Does the watch give correct time during the free fall?
(d) What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity? View SolutionQuestion 19
One end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion. View SolutionQuestion 20
An air chamber of volume v has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction. Show that when the ball is pressed down a little and released for the time priod of oscillation, assuming pressure-volume variations of the air to be isothermal. View SolutionQuestion 21
You are riding an automobile of mass 3000kg. Assuming that you are examining the oscillation characteristics of its suspension system. The suspension sags 15cm when the entire automobile is placed on it. Also, the amplitude of oscillation decreases by50% during one complete oscillation. Estimate the values of (a) the spring constant k and (b) damping constant b for the spring and shock absorber system of one wheel, assuming that each wheel supports 750kg.g=10m/s2. View SolutionQuestion 23
A circular disc of mass 10kg is suspended by a wire attahced to its centre. The wire is twisted by rotating the disc and released. The period of torsional oscillations is found to be 1.5s. The radius of the disc is 15cm. Determing the torsional spring constant of the wire. (Torsional spring constant α is definied by the relation J=−αθ, where J is the restoring coubple and θ the angle of twist.View SolutionQuestion 25
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t=0. Determine the amplitude of the resulting oscillations in terms of the parameters ω,x0andv0. View SolutionQuestion 59
Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2∘ to the right with the vertical , the other pendulum makes an angle of 1∘ to the left of the vertical. What is the phase difference between the pendulums?View Solution
All Exercises from MODERN PUBLISHERS PHYSICS (HINGLISH) Class 11 PHYSICS OSCILLATIONS
- PRACTICE PROBLEMS
- PRACTICE PROBLEMS 2
- CONCEPTUAL QUESTIONS
- TOUGH & TRICKY PROBLEMS
- NCERT (ADDITIONAL EXERCISES)
- NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTION ( SHORT ANSWER TYPE QUESTIONS )
- NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTION (MULTIPLE CHOICE QUESTIONS (TYPE-I))
- NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTION (MULTIPLE CHOICE QUESTIONS (TYPE-II))
- NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTION (VERY SHORT ANSWER TYPE QUESTIONS )
- NCERT FILE (TEXTBOOK EXERCISES)
- HOTS (HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL)
- REVISION EXERCISES (ADDITIONAL QUESTION )
- REVISION EXERCISES (FILL IN THE BLANKS)
- REVISION EXERCISES (LONG ANSWER QUESTIONS)
- REVISION EXERCISES (NUMERICAL PROBLEMS)
- REVISION EXERCISES (SHORT ANSWER QUESTIONS)
- REVISION EXERCISES (VERY SHORT ANSWER QUESTIONS)
- COMPETITION ASSERTION REASON TYPE QUESTIONS
- COMPETITION (INTEGER TYPE QUESTIONS)
- COMPETITION FILE (JEE (ADVANCED) FOR IIT ENTRANCE)
- COMPETITION FILE (MATCHING TYPE QUESTIONS)
- COMPETITION FILE (MATRIX MATCH TYPE QUESTIONS)
- COMPETITION FILE (MULTIPLE CHOICE QUESTION)
- COMPETITION FILE (MULTIPLE CHOICE QUESTION) BASED ON A GIVEN PASSAGE/COMPREHENSION
- COMPETITION FILE (MULTIPLE CHOICE QUESTION) JEE (MAIN) & OTHER STATE BOARDS FOR ENGINEERING ENTRANCE
- COMPETITION FILE (MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE (MULTIPLE CHOICE QUESTIONS) AIPMT/NEET OTHER STATE BOARDS FOR MEDICAL ENTRANCE
- PRACTICE TEST (FOR BOARD EXAMINATION)
- SOLVED EXAMPLES