In exercise 14.9 let us take the position of mass when the spring is unstretched as x = 0, and the direction from left to right as the positive direction of X-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is
(a) at the mean position.
(b) at the maximum stretched position, and
( c ) at the maximum compressed position.
IN what way do these functions for SHM differ from each other, in frequency in amplitude or the initial phase ?
a=2cm,ω=√km=√12003=20rads−1
(a) When mass is at mean position
Then x =a sin ωt
x = 2 sin 20 t
(b) At maximum stretched position the mass is at extreme right position, hence, initial phase is π2
∴x=asin(ωt+π2)
=2cosωt=2cos20t
(c ) At maximum compressed position, the mass is at extreme left with initial phase of 3π2 rad.
∴x=asin(ωt+π2)
=2cosωt=2cos20t
(c ) At maximum compressed position, the mass is at extreme left with initial phase of 3π2 rad.
∴x=asin(ωt+3π2)
=−acosωt=−2cos20t
Thus these functions differ in intial phase.
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT (Additional Exercises)
6 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT Exemplar Problems Subjective Question (Multiple Choice Questions (Type-I))
11 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - TOUGH & TRICKY PROBLEMS
9 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
In example 34, let us take the position of the mass, when the spring is unstretched, as x=0, and the direction from left to right as the positive direction of X-axis. Give x as a function of time t for the oscillating mass, if at the moment we start the stop watch (t=0), the mass is (i) at the mean position (ii) at the maximum stretched position (iii) at the maximum compressed position.
In what do these different functions of SHM differ ? Frequency, amplitude or initial phase ?
View SolutionAn impulsive force gives an initial velocity of −1.0ms−1 to the mass in the unstretched spring position. What is the amplitude of motion ? Give x as a function of time for the oscillating mass. Given m=3 kg, k=1200Nm−1
View Solution
Knowledge Check
The inclination of the line x−y+3=0 with the positive direction of x-axis is
A45∘B135∘C−45∘D−135∘The inclination of the line x−y+3=0 with the positive direction of x-axis is :
A45∘B135∘C−45∘D−135∘Find out the position of particle as a function of time which is moving in a straight line with an acceleration a=5x, where x is position.
(i) At t=0 the particle is at x=0 (ii) Mass of the object is 5kgAQuestion can be solved by information I only.BQuestion can be solved by information II onlyCQuestion can be solved by information I and II in combined form only.DQuestion can not be solved by both the informations only.
An impulsive force gives an initial velocity of- 1.0ms−1 to the mass in the unstretched spring position [sec Fig. 16.2]. What is the amplitude of motion ? Give x as a function of time t for the oscillating mass. Given m=3 kg and k=1200Nm−1.
View SolutionFind out the position of particle as a function of time which is moving in a straight line with an acceleration a=5x, where x is position.
(i) At t=0 the particle is at x=0 (ii) Mass of the object is 5kg
View SolutionA car is moving on a straight road. The velocity of the car varies with time as shown in the figure. Initially (at t=0), the car was at x=0, where, x is the position of the car at any time 't'.
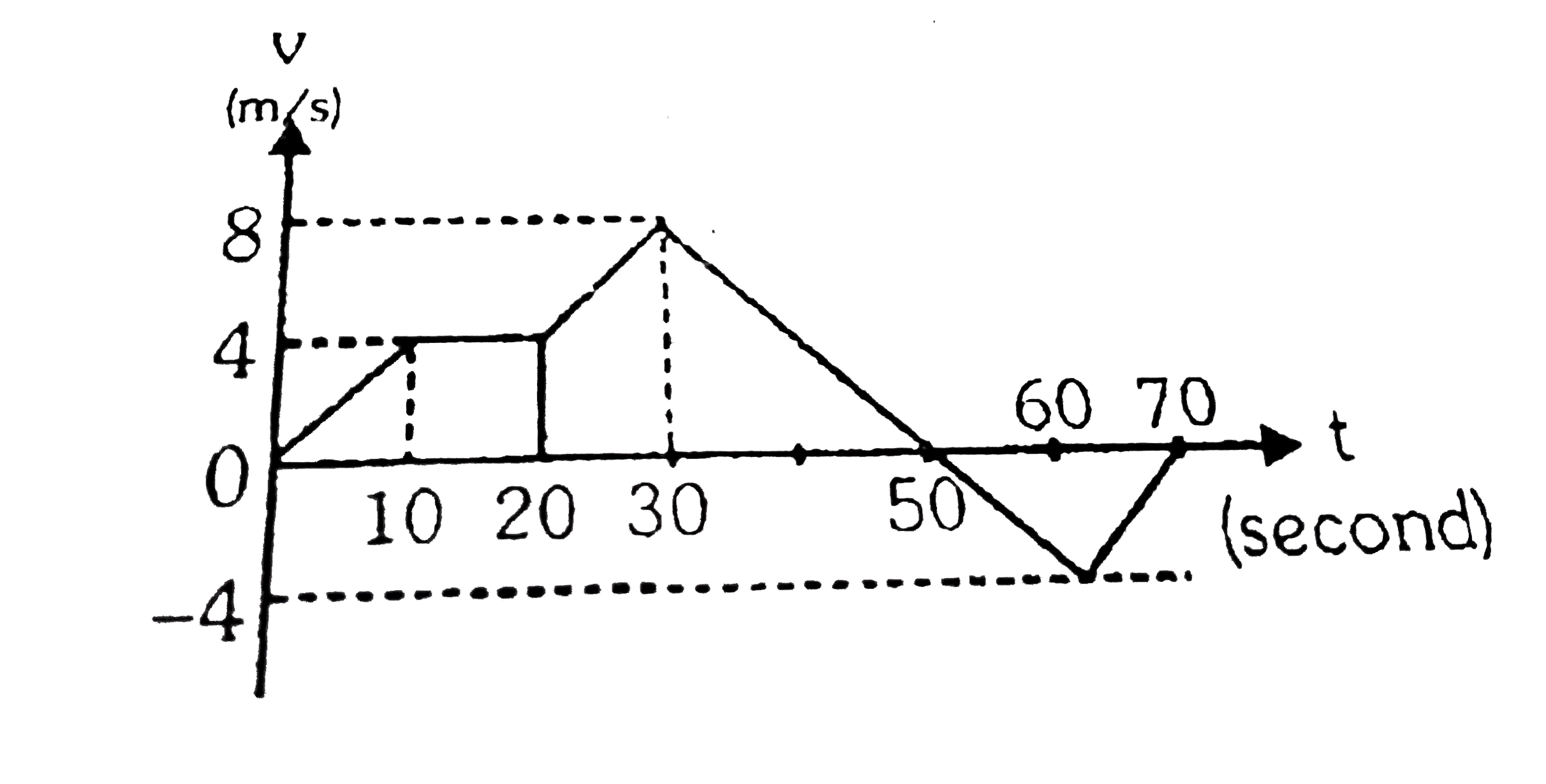
The maximum displacement from the starting position will be :-
View SolutionA car is moving on a straight road. The velocity of the car varies with time as shown in the figure. Initially (at t=0), the car was at x=0, where, x is the position of the car at any time 't'.

The maximum displacement from the starting position will be :-
View SolutionA particle A of mass 10/7kg is moving in the positive direction of x−aξs. At initial position x=0, its velocity is 1ms−1, then its velocity at x=10m is (use the graph given)

View Solution
