6 Long answer (NCERT) from PRADEEP PHYSICS Chapter 3 KINEMATICS for Class 11
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| PRADEEP PHYSICS | 6 Long answer (NCERT) |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
A hill is 500m hight. Supplies are to be across the hill using a canon that can hurl packetets at a speed of 125m/s pver the hill . The canon is located at a distance of 800m from the foot to hill and can be veoved on the ground at a speed of 2m/s,sotˆitsdistanceomthehillcanbeadjusted.Wˆistheshortesttime∈whichapachetcanreachonthegroundacrossthehill?Taje g= 10 m//s^2.View SolutionQuestion 2
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R=v20g. If a target farther away by distance Δx (beyond R) has to be hit with the same gun, show that it could that it could be achieved by raising the gun to a height at least h=Δx[1+ΔxR]
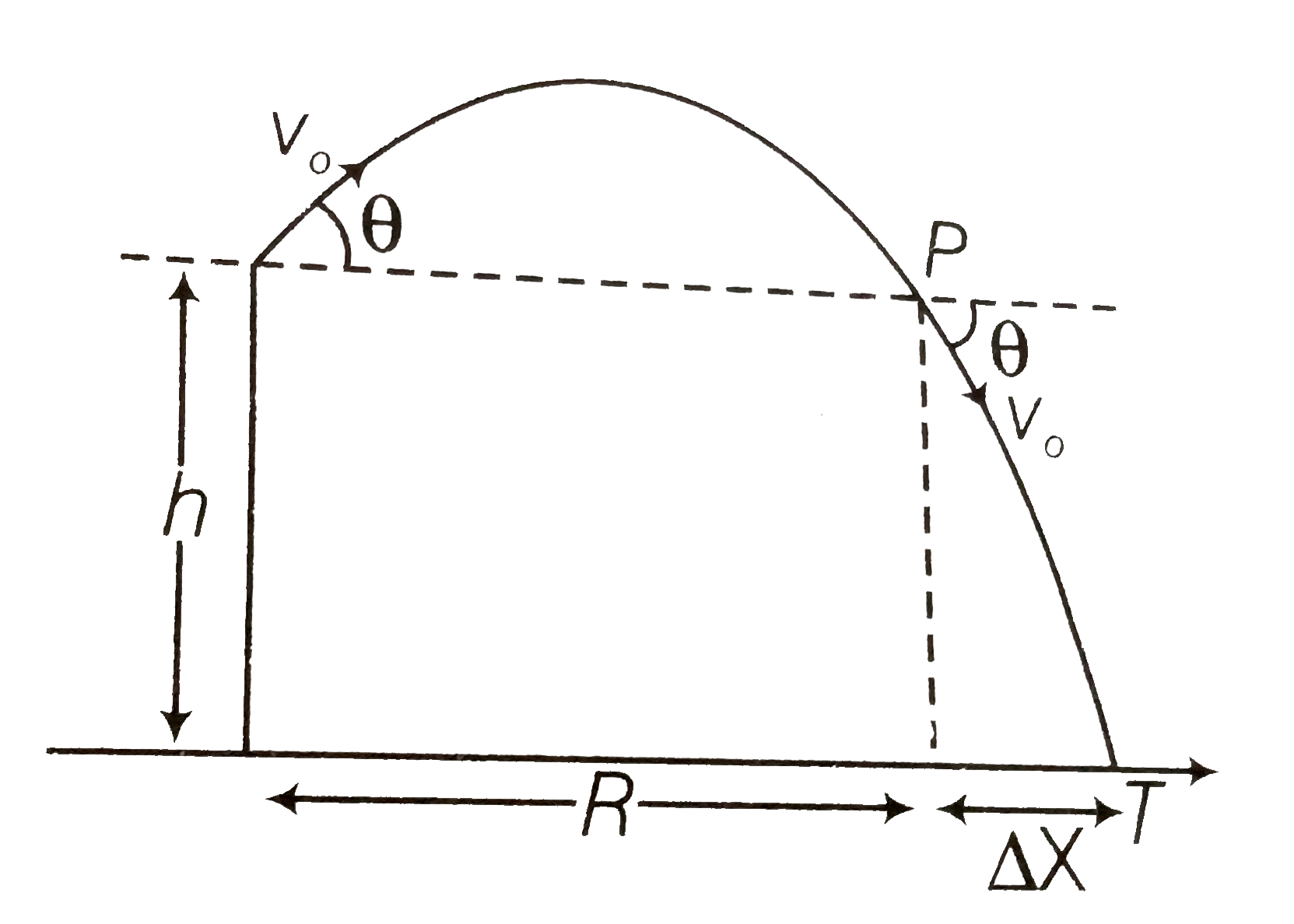 View Solution
View SolutionQuestion 3
A particle is projected in aer an angle β to a surface which itself is inclined at an angle α to the horixonta (Fig. 2 (EP). 26)
(a) Find an ecxpression for range on the plane surface (distanc eon the plance from the point of projection at which particle will hit the surface). (b) Time of flight. 9c ) β at which range will be maximum.
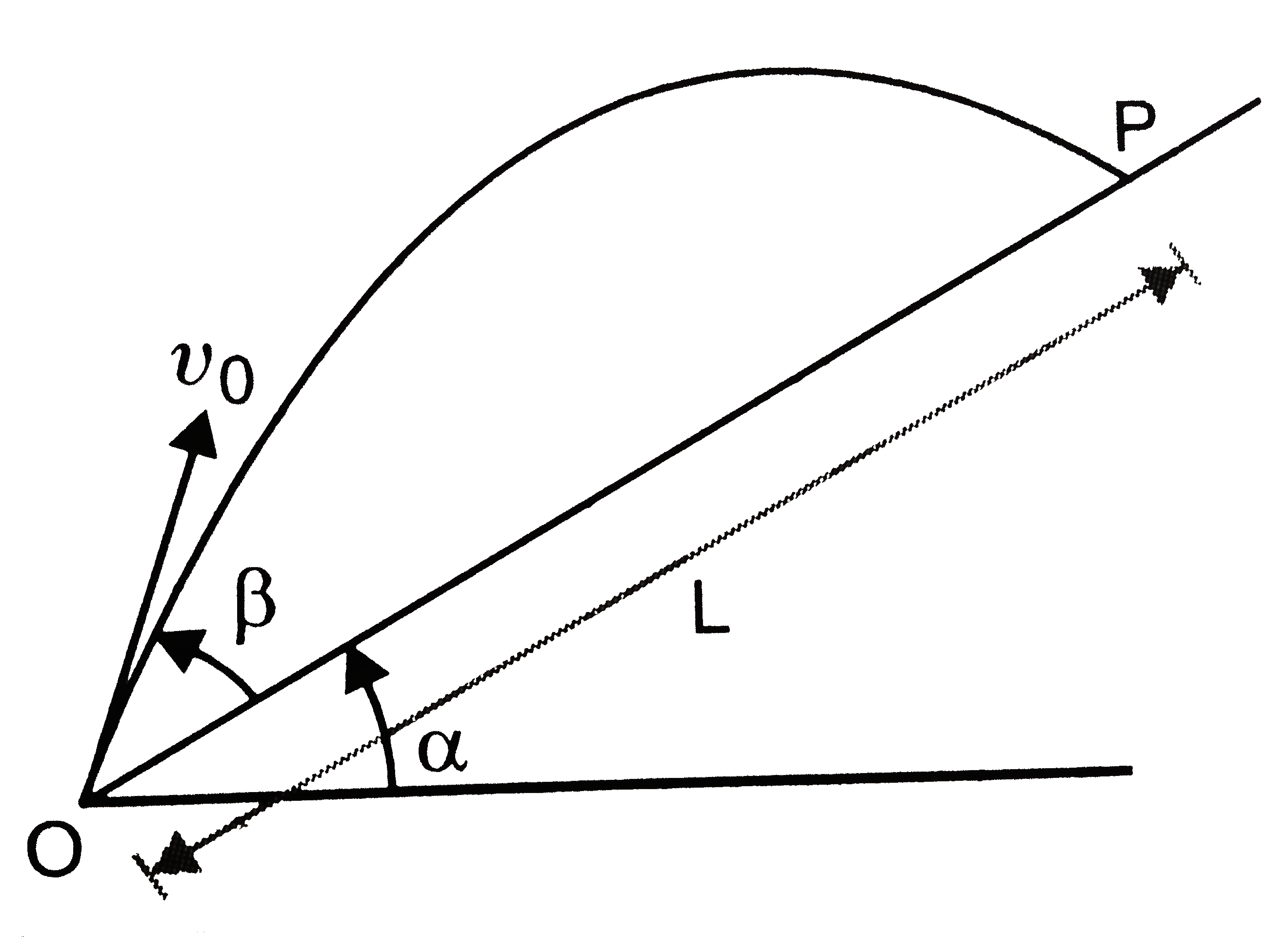 View Solution
View SolutionQuestion 5
A girl riding a bicycle with a speed of 5m/s to wards Noth direction, observes rain falling vertically down. If she increases her speed to 10m/s, rain appeard to meet her at 45∘ to the vertical . What is the speed ot the rain ? In what direction does rain fall as observed by a ground based observer ?View SolutionQuestion 6
A river is flowing due east with a speed 3m/s (Fig. 2 (EP) .31 ).
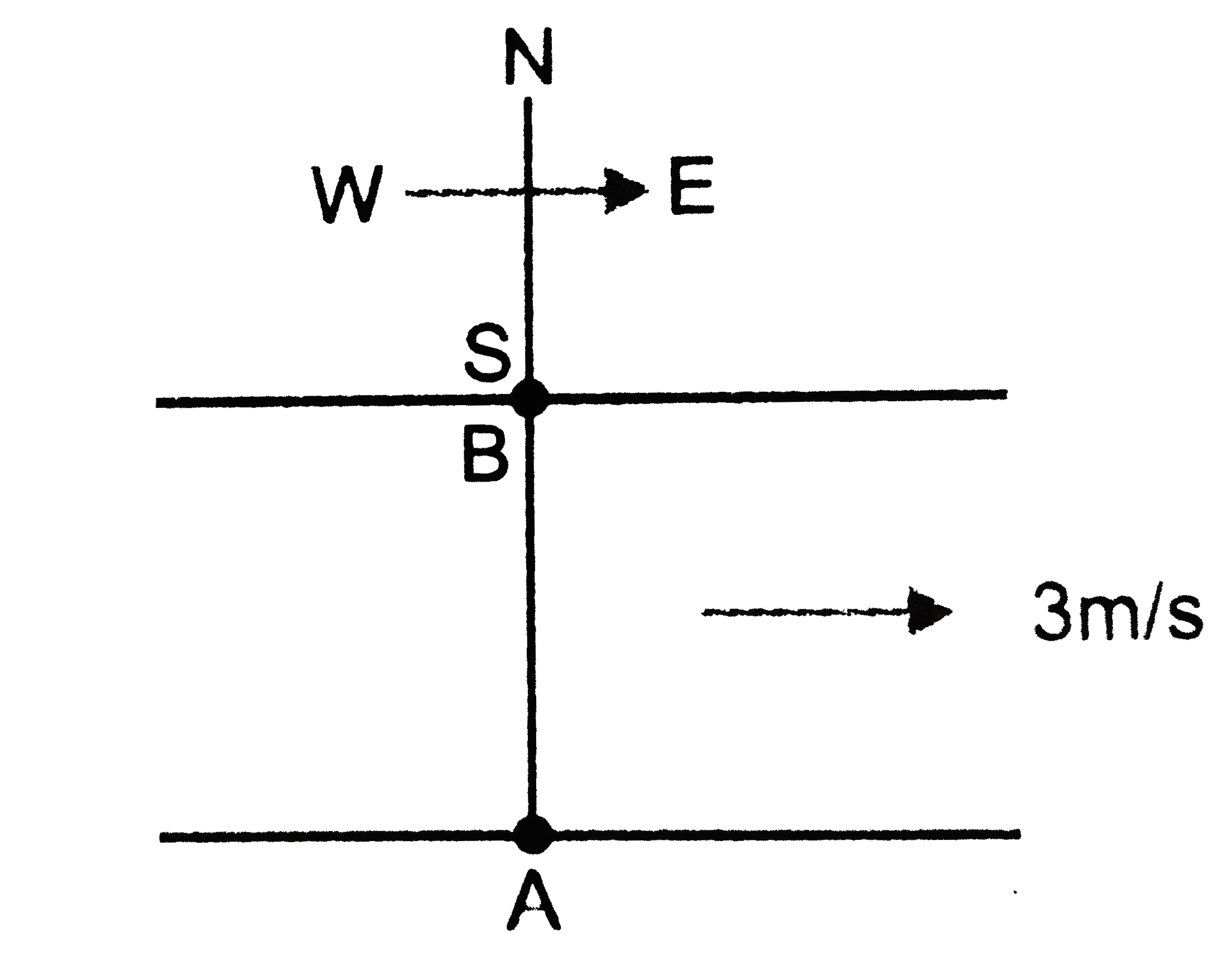 . (a) If swimmer starts swimming due borth, what will be his resultant velocity (magnitude and direction) ? (b) If he wants to start from point (A) on South bank and reach opposite point (B) on North bank,
. (a) If swimmer starts swimming due borth, what will be his resultant velocity (magnitude and direction) ? (b) If he wants to start from point (A) on South bank and reach opposite point (B) on North bank,
(i) Which direction should he swim? (ii) What will be his resultant speed ? (c ) From two differenrent casses as mentioned in (a) and 9b) above, in which casse will he reach opposite bank in shorter time ?View SolutionQuestion 7
A cricket fielder can throw the cricket ball with a speed v0. If he throws the ball while running with speed (u) at angle θ to the horizontal, find
(b) what will be time of flight ?
(c ) what is the distance (horizontal range) form the point of projection at which the ball will land ?
(d) find θ at which he should throw the ball that would maxmise the horizontal range range as found in (c ).
(e) how does θ for maximum range change if u gt v_0, u=v_0, ult v_0 ?
(f) how does θ in (e) compare with that for u=0 (i.e., 45^@) ?View SolutionQuestion 8
Motion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian coordinates A=Axˆi+Ayˆj, where ˆi and ˆj are unit vector along x and y-directions, respectively and Ax and Ay are corresponding components of A. Motion can also be studied by expressing vectors in circular polar coordinates as A=Arˆr+Aθˆθ, where ˆr=rr=cosθˆi+sinθˆj and ˆθ=−sinθˆi+cosθˆj are unit vectors along direction in which r and θ are increasing.
(a) Express ˆi and ˆj in terms of ˆr and ˆθ.
(b) Show that both ˆr and ˆθ are unit vectors and are perpendicular to each other.
(c) Show that ddt(ˆr)=ωˆθ, where ω=dθdt and ddt(ˆθ)=−θˆr.
(d) For a particle moving along a spiral given by r=aθˆr, where a = 1 (unit), find dimensions of a .
(e) Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.
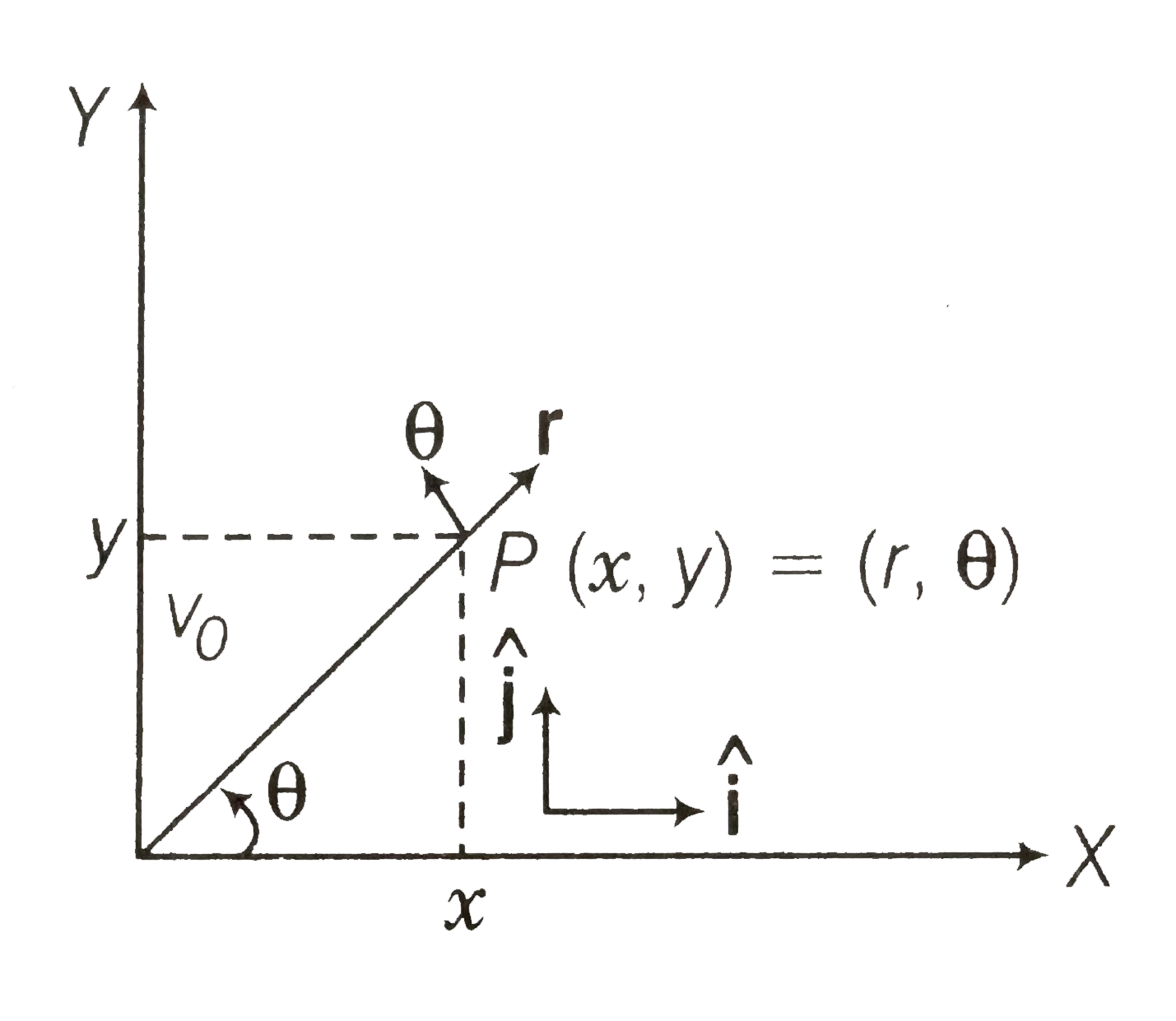 View Solution
View SolutionQuestion 9
A man wants to reach from A to the opposite corner of the square C. The sides of the square are 100 m. A central square of 50m×50m is filled with sand. Outside this square, he can walk at a speed 1 m/s. In the central square , he can walk only at a speed of v m/s (v<1). What is smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand ?
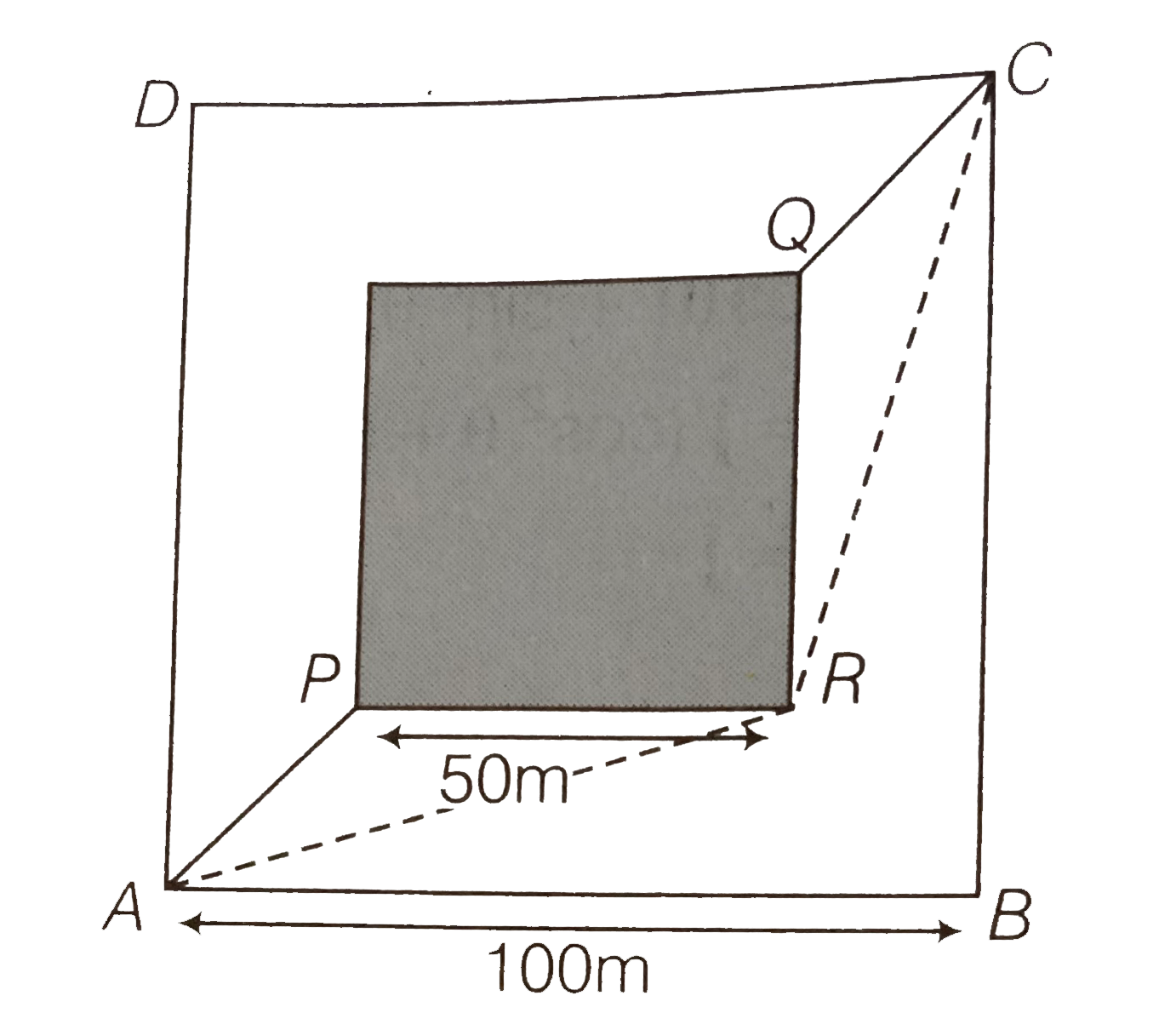 View Solution
View Solution
All Exercises from PRADEEP PHYSICS Class 11 PHYSICS KINEMATICS
- 1 Problems for practice
- 1 Con ceptual Problems
- 1 Conceptual Problems
- 1 Fill in the blanks
- 1 Long answer
- 1 Multiple choice
- 1 NCERT Assertion-Reaseon Type
- 1 NCERT Comprehension
- 1 NCERT multiple
- 1 Short answer
- 1 SolvedExamples
- 1 Very short
- 2 Con ceptual Problems
- 2 Fill in the blanks
- 2 Long answer
- 2 Multiple choice
- 2 NCERT multiple
- 2 Problems for practice
- 2 Short answer
- 2 SolvedExamples
- 2 Very short
- 3 Con ceptual Problems
- 3 Fill in the blanks
- 3 Long answer
- 3 Multiple choice
- 3 NCERT multiple
- 3 Problems for practice
- 3 Short answer
- 3 SolvedExamples
- 3 Very short
- 4 Con ceptual Problems
- 4 Conceptual Problems
- 4 Fill in the blanks
- 4 Long answer
- 4 Multiple choice
- 4 NCERT Integer type
- 4 NCERT multiple Choice
- 4 Problems for practice
- 4 Short answer
- 4 SolvedExamples
- 4 Very short
- 5 Long answer (NCERT)
- 5 Short answer
- 5 Very short
- 6 Long answer (NCERT)
- 6 Short answer
- 6 Very short
- Additional Exercises
- Advanced Problems
- Higher order thinking skills
- Motion
- NCRT Exercises
- Sample Promlem
- Value based
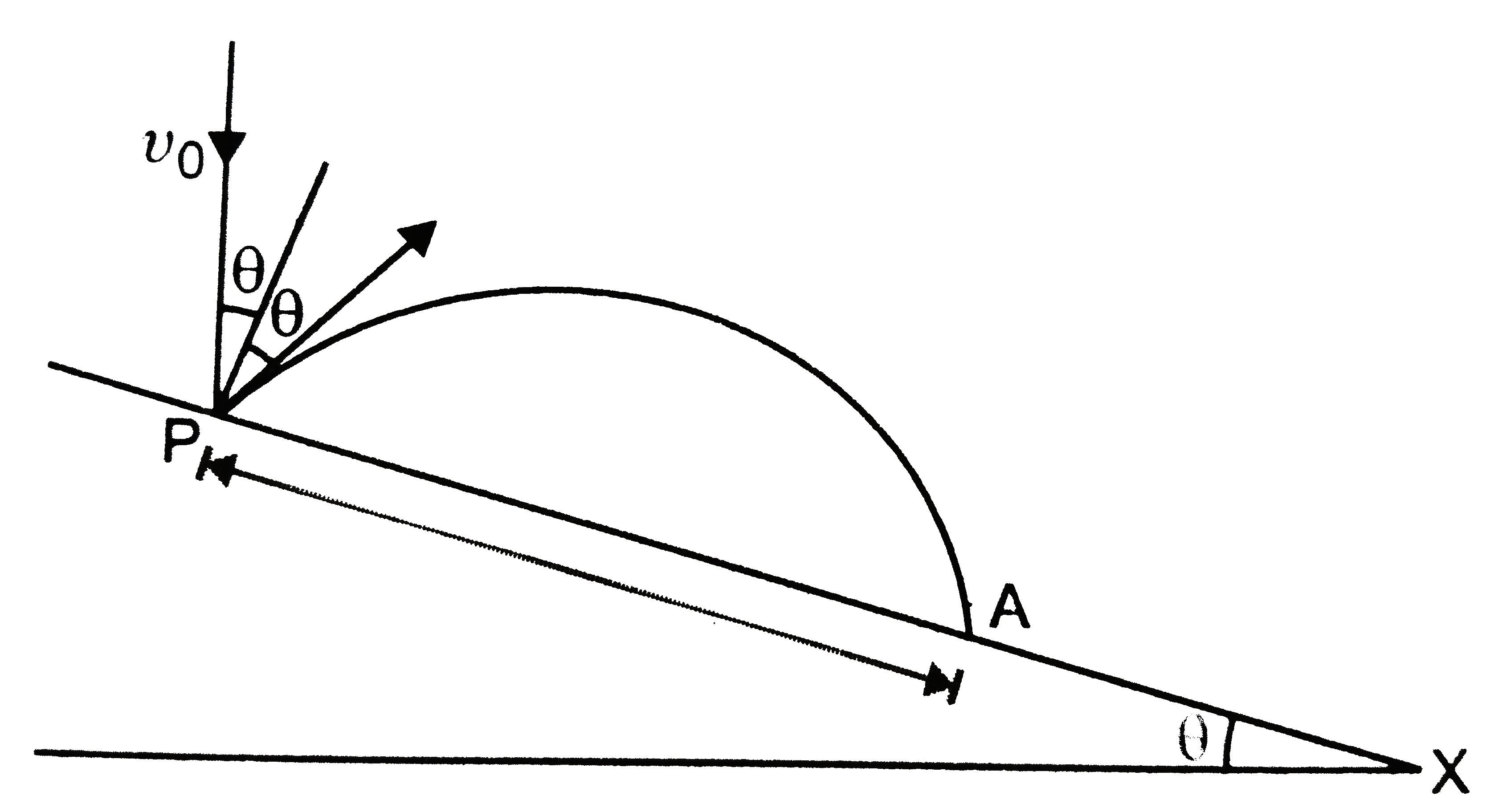 .
.