APPLICATION OF INTEGRALS AND AREA UNDER THE CURVE for Class 12 MATHS
Introduction
Hello Students, In today's class we will learn a very interesting topic which is Application of Integrals and Area under curve which has a good weightage in the exam of JEE.
These notes are designed keeping in mind the basics and the recent changes in the syllabus and pattern of JEE.
You can follow Doubtnut for all the videos related to JEE 2022.
In geometry, we have studied the calculation formulas of various geometric numbers including triangles, rectangles, trapezias and circles. Such formulas fundamental to the use of mathematics for many real health problems. Basic geometry formulas allow us to calculate many simple mathematical locations. However, they are not enough to count places curved curves. So we will need some ideas of Integral Calculus. In the preceding chapter, we learned how to find bounded curve y = f (x), editing x=a,x=b and x-axis, while calculating clear interactions such as amount limit. Here, in this chapter, we will learn in particular the use of combinations to find space under easy curves, the space between the lines and the arcs of circles, parabolas and ellipses (common forms only). We will deal with adoption the area bound by the curves mentioned above.
Index
Basic concept and Definition|Cases of area bounded by different curves on x-axis|Cases of area bounded by different curves on y-axis|Area enclosed by different figures|Shifting of origin|Curve Tracing|Equation in Parameteric form|Average value of a function|Area bounded by Inverse
Basic concept and Definition
In the previous chapter, we have studied definite integral as the limit of a sum and how to evaluate definite integral using Fundamental Theorem of Calculus. Now, we consider the easy and intuitive way of finding the area bounded by the curve y=f(x),x-axis and the ordinates x=a and x=b we can think of area under the curve as composed of large number of very thin vertical strips. Consider an arbitrary strip of height y and width dx, then dA (area of the elementary strip)= ydx, where, y=f(x). Calculating area of some complex figures requires integration.
We usually have a curve having function of either x or y and integrating them on opposite variable represented as
∫ydx or ∫xdy
Cases of area bounded by different curves on x axis
- The area bounded by curve y=f(x) , axis of x and the ordinates x=a and x=b (where b>a) is given by A=∫baf(x)dx=∫baydx

- The area bounded by the straight line x=a , x=b (where a<b) and the curves y=f(x) and y=g(x) , provided f(x)<g(x) where x=a is lower limit and x=b is Upper limit.
A=∫ba[g(x)−f(x)]dx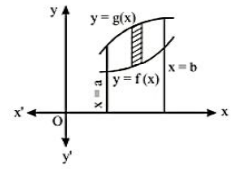
- When two curves y=f(x) and y=g(x) intersect , the bounded area is given as A=∫ba[g(x)−f(x)]dx
which is same as above the only difference is we can find the limit by equating g(x)=f(x)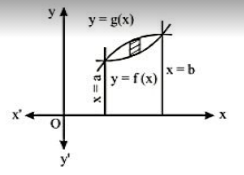
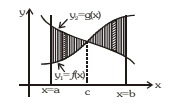
- If the curves y1=f(x) and y2=g(x) intersect at x=c , then required area.
A=∫ca(g(x)−f(x))dx+∫bc(f(x)−g(x))dx=∫ba|(f(x)−g(x))|dx
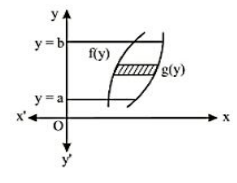
Cases of area bounded by different curves on y axis
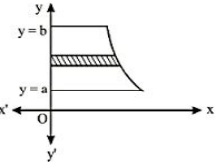
- The area bounded by curve x=f(y) , axis of y and the ordinates y=a and y=b (where b>a) is given by A=∫baf(y)dy=∫baxdy
- The area bounded by the straight line y=a , y=b (where a<b) and the curves x=f(y) and x=g(y) , provided f(y)<g(y) where y=a is lower limit and y=b is Upper limit.
A=∫ba[g(y)−f(y)]dy - When two curves x=f(y) and x=g(y) intersect , the bounded area is given as A=∫ba[g(y)−f(y)]dy
which is same as above the only difference is we can find the limit by equating g(y)=f(y) - If the curves x1=f(y) and x2=g(y) intersect at y=c , then required area.
A=∫ca(g(y)−f(y))dy+∫bc(f(y)−g(y))dy=∫ba|(f(y)−g(y))|dy

Example 1
The area bounded by the curve y=[x264+2],y=x−1,y=x−1andx=0 above the x-axis will be-(Where [] represents greatest integer function)
We have,
0≤x264<1,if−1<x<8
⇒2≤x264+2<3,if|x|<8
⇒y=[x264+2]=2,if|x|<8
The graphs of the given curves is as shown in Fig. 6.

Let required area be A. Then,
A= Area of the shaded region
⇒A=2∫0xdy=2∫0(y+1)dy
⇒A=12[(y+1)2]20=92−12=4 sq. units.
Example 2
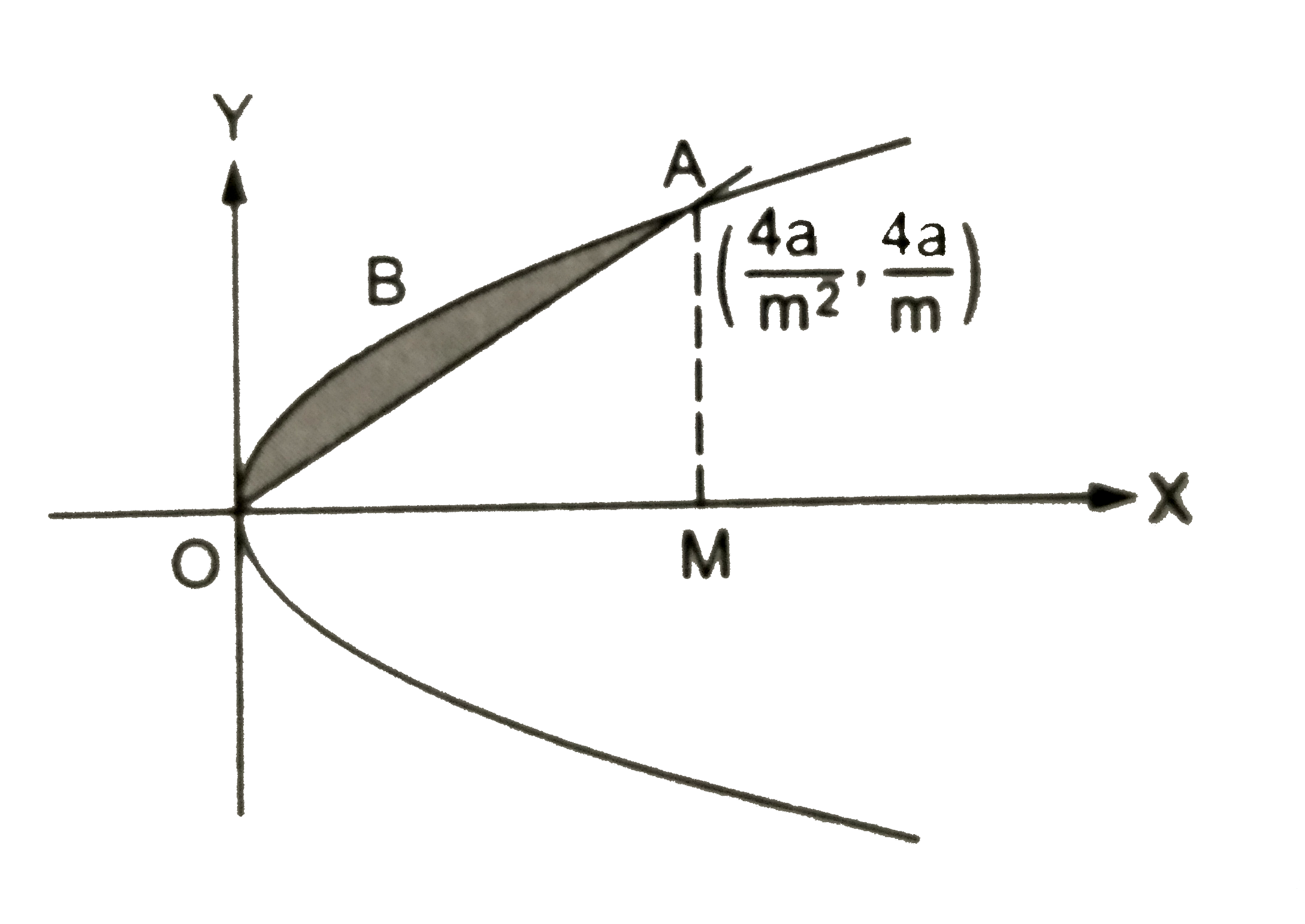
Find the area enclosed between the parabola y2=4ax and the line y=mx.
The given equation are
y2=4ax …(i)
and y=mx ...(ii)
Clearly y2=4ax is a right handed parabola passing through the origin And y=mx is a line passing through the origin .
In order to find points of intersection of the given parabola and putting y=mx from (i) and (ii) simultaneously
Putting y=mx from (ii) into (i) we get
m2x2=4ax⇒4ax⇒x(m2x−4a)=0
⇒x=0orx=4am2
Now (x=0⇒y=0)and(x=4am2⇒y=4am)
So , the points of intersection of the given parabola and the chord are
O(0,0)andA(4am2,4am)
Draw AM⊥OX
Required area = (area OBAMO)=(area OAMO)
=4a/m2∫0(y for the parabola ) dx=4a/m2∫0(y for the line )dx
=4a/m2∫02√axdx=4a/m2∫0mxdx
=2√a.23[x3/2]4a/m20=[mx22]4a/m20
=[4√23.8m3a3/2=m2.16a2m4]
=(32a23m2−8a2m3)=(8a23m2)sq units
Hence , the required area is (8a23m2) sq units .
Example 3
Find the area bounded by the curve y=sinx between x=0 and x=2π .
The given curve is y=sinx
Some values of x and the corresponding values of y are given below :
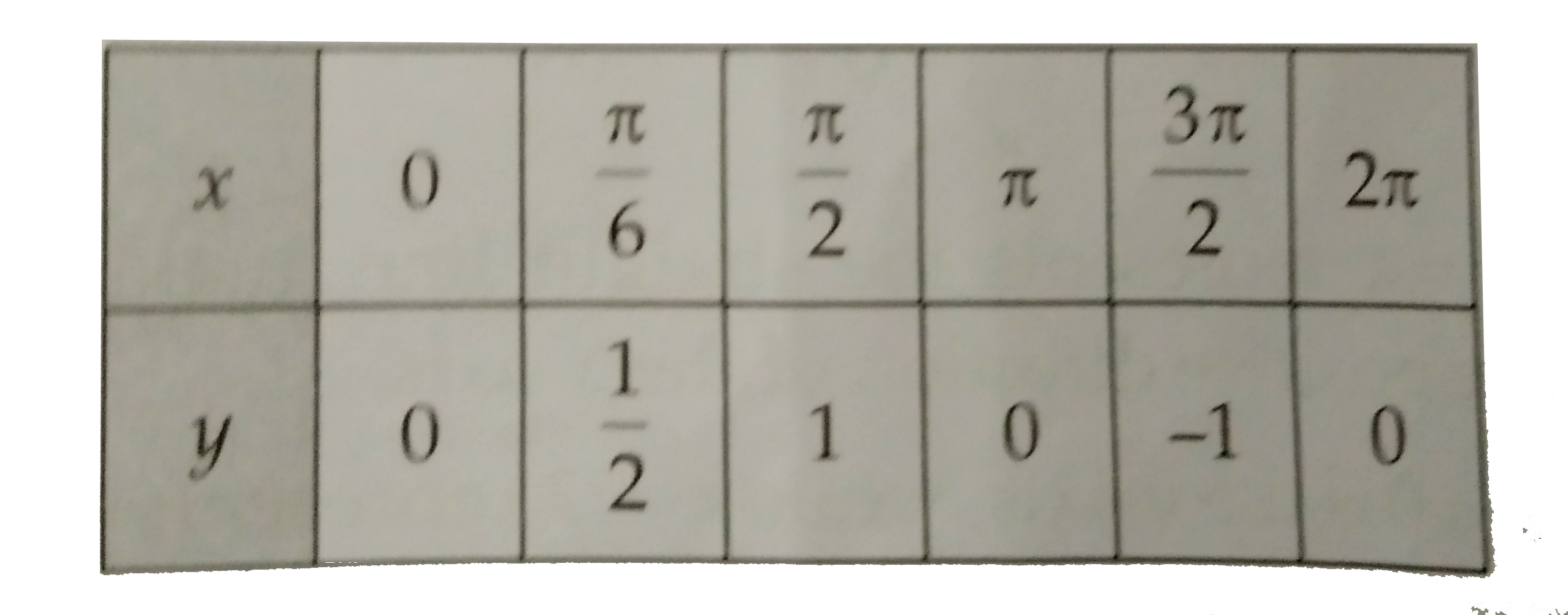
Taking a fixed unit (distance ) lfor π along the x-axis , we can plot the points (0,0)(π6,12),(π2,1),(π,0)(3π2,−1)and(2π,0)
Join these points freehand to obtain a rough sketch of the given curve.
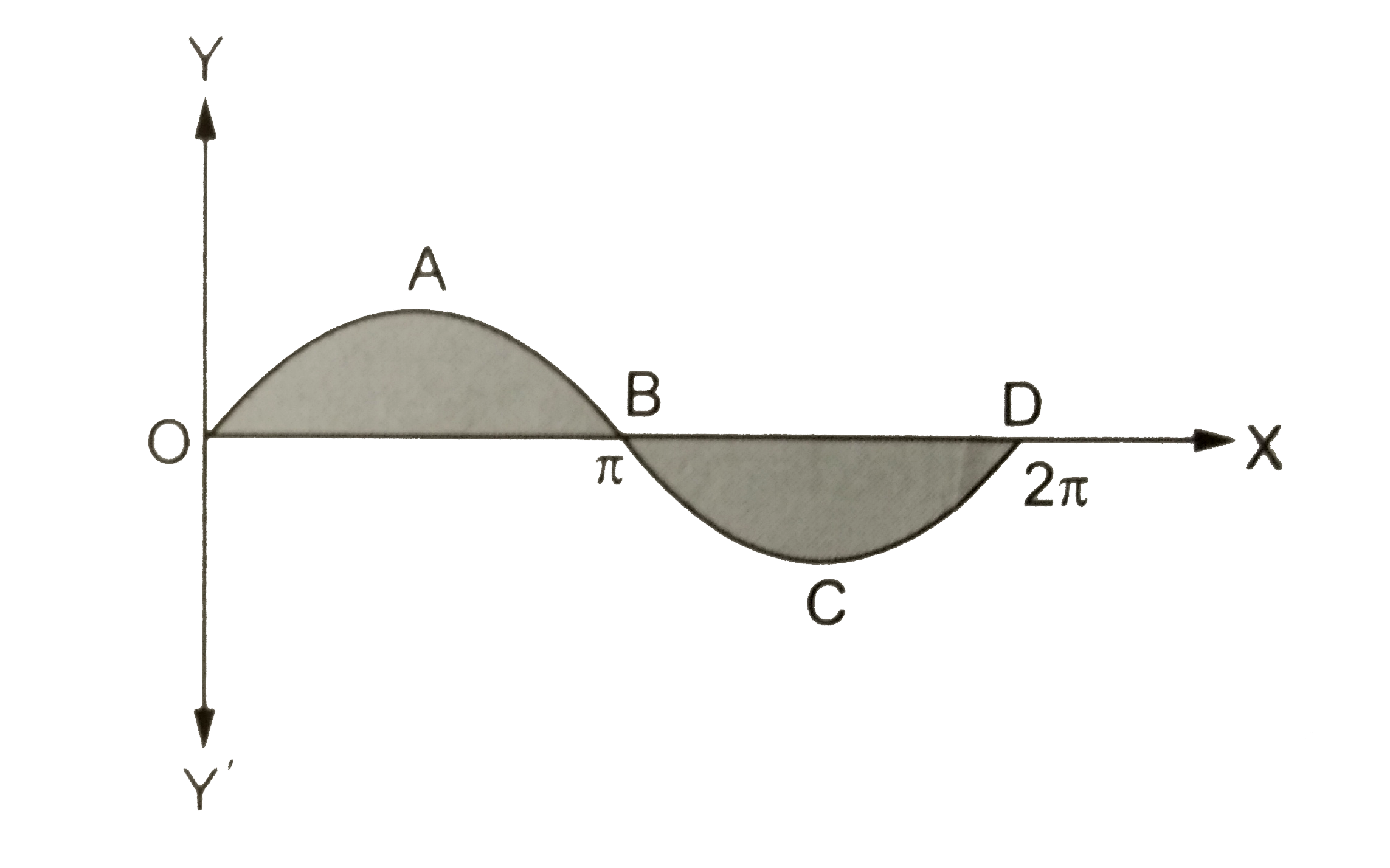
Required area = (area OABO ) + (area BCDB)
=π∫0y dx + 2π∫π(−y)dx[∵ area BCDB is below the x-axis ]
=π∫0sinxdx−2π∫πsinxdx
=[−cosx]π0−[−cosx]2ππ=(2+2)=4 sq units
Hence , the required area is 4 sq units.
Example 4
Find the area of the region bounded by the curve y2=2y−x and the y-axis.
y2=2y−x⇒y2−2y=−x
⇒y2−2y+1=−x+1
⇒(y−1)2=−(x−1)
⇒Y2=−X

This is a left-handed parabola with vertex at (X=0,Y=0) .
X=0,Y=0 ⇒−x+1=0andy−1=0
⇒x=1andy=1
Thus , the vertex of the given parabola is A(1,1) Also x=0→y2=0⇒y(y−2)=0⇒y=0ory=2
Thus , the curve meets the y-axis at O(0,0) and B(0,2)
a rough sketch of the curve can be drawn,as shown in the firgue .
∴ required area =2∫0x dy =2∫0(2y−y2)dy
=[y2−y33]20=(4−83)=43 sq units
Hence , the required area is 43 sq units
Example 5
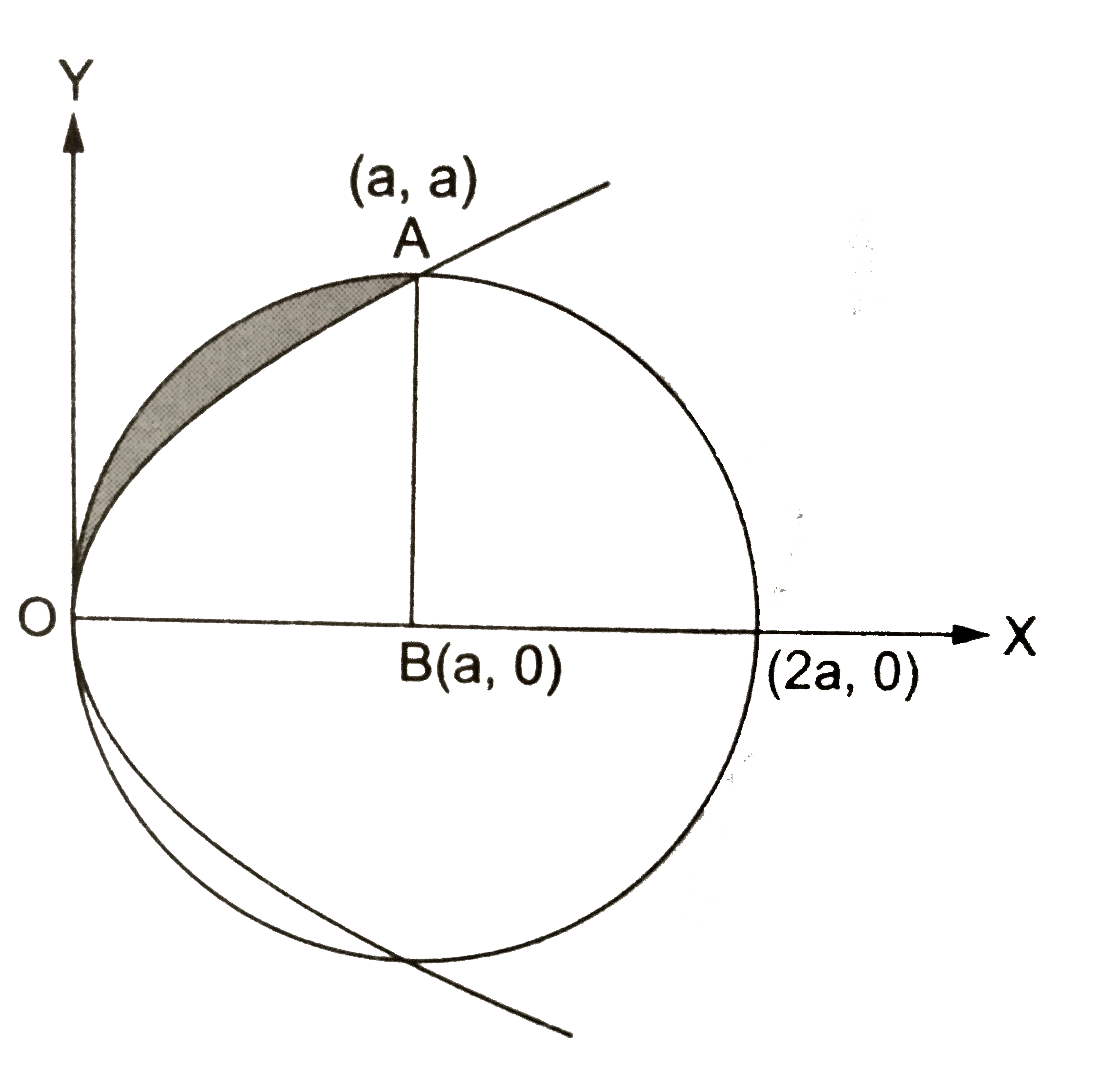
Find the area of the region {(x,y):x2+y2≤2ax , y2≤ax , x≤0 , y≤0}
Clearly we have to find the area of the region lying in the first quadrant (x≥0,y≥0) included between the circle x2+y2=2ax and the parabola y2=ax
Thus , the equations of the given curves are
x2+y2=2ax…(i)
and y2=ax ...(ii)
Now , clearly x2+y2=2ax is a circle with its center B(a,0) and radius =a units
And y2=ax is parabola with O(0,0) as its vertex and the x-axis as its axis. We can draw its figure as shown .
Their points of intersection may be obtained by solving (i) and (ii) and keeping in view that x≥0andy>0
Using (ii) in (i) ,we get
x2−ax=0⇒x(x−a)=0
⇒x=0orx=a
Now (x=0⇒y=0) and (x=a⇒y=a)
Thus, two curves intesect at O(0,0) and A(a,a)
∴ required area =a∫0√2ax−x2dx−a∫0√axdx
=a∫0√a2−(x−a)2dx−√a.a∫0√xdx
=⎡⎢
⎢⎣(x−a)√a2−(x−a)22+a22sin−1(x−aa)⎤⎥
⎥⎦a0−√a[23x3/2]a0
={a22sin−1(0)−a22sin−1(−1)−23a2}
=(πa24−23a2)sq units
Hence, the required area is =(πa24−23a2) sq units .
Example 6
Find the area of the circle x2+y2=a2 with radius a
x2+y2=a2
The centre of this circle is (0, 0) and radius is 'a'. X−andY− axes divide the circle into 4 symmetric parts.
Now, x2+y2=a2
⇒y=±√a2−x2
In first quadrant,
y=√a2−x2

Co-ordinates of points O and A are (0, 0) and (a, 0) respectively. Now area of region bounded by the circle, X-axis, x = 0 and x = a
= Area of OABO
=∫a0y dx=∫a0√a2−x2dx
=[x2√a2−x2+a22sin−1xa]a0
=(0+a22sin−11)−(0+0)
=a2π2×2=14πa2
∴ Area of circle =4×Area of OABO
=4×14πa2=πa2sq. units.
Area enclosed by different figures
The equation of Ellipse is x2a2+y2b2=1 and area bounded under the curve is
Here A=∫ydx
A=4∫a0(b√1−a2x2)dx [Let x=asinθ]
A=4∫π20(abcos2θ)d(θ)
⇒4ab∫π20(cos2θ)d(θ)
4ab∫π201+cos2θ2d(θ)
⇒4ab(π4)=πab
Similarly
- Area enclosed by a parabola y2=4ax and x2=4by is 16ab3 sq. units
- Area included between the parabola y2=4ax & the line y=mx is 8a23m3 sq. units.
- The area of the region bounded by one arc of sinax(orcosbx) and x-axis is 2a sq. units.
Example 7
Find the area of the smaller region bounded by the ellipse x2a2+y2b2=1and the line xa+yb=1
We can use the above result to calculate Area
Area of ellipse in the first quadrant will be πab4 and area of triangle is ab2
∴Area=πab4−ab2
Alternate
x2a2+y2b2=1
y=ba√a2−x2 ...(1)
xa+yb=1⇒y=ba(a−x) ...(2)
The points of intersection of the ellipse x2a2+y2b2=1 and straight line xa+yb=1 are A(a,0)andB(0,b).
Draw the graphs of both.

Now required area
=ar(OAPBO)−ar(OAQBO)
=∫a0ba√a2−x2dx−∫a0ba(a−x)dx
=ba[x2√a2−x2+a22sin−1xa]a0−ba[ax−x22]a0
=ba[(0+a22⋅π2)−(0+0)]−ba[(a2−a22)−(0−0)]
=(πab4−ab2) sq. units.
Shifting of origin
While calculating area of a region using definite integral. Sometimes it is more convenient to evaluate the required area by shifting the given curves with respect to the origin. It may be seen that the original functions are given in their general form and their manipulation, in order to find the area, is a little bit lengthy.
Although if we shift the curve with respect to the origin. Then we get the equation of these curves in their standard form. So it could be much easier to manipulate the shifted curves to find the area.
Example 8
Area enclosed between the parabolas y2−2y+4x+5=0andx2+2x−y+2=0
y2−2y+1⇒(y−1)2=−4(x+1) ...(i)
x2+2x+1=y−1⇒(x+1)2=(y−1) ...(ii)
Let y−1=Yandx+1=X
So the equation of parabola is Y2=−4XandX2=Y
a=1andb=14
So the Final area =16ab3=(163)⋅1⋅(14)=43
Example 9
Find by integration the area of the region bounded by the curve y=2x−x2 and the x-axis.
The given curve is y=2x−x2
Now y=2x−x2⇒(x2−2x+1)=(−y+1)
⇒(x−1)2=−1(y−1)
⇒X2=−y
where (x−1)=Xand(y−1)=y
Clearly , x2=−y is a downward parabola with its vertex at (X=0,Y=0).
Now , X=0,Y=0⇒x−1=0andy−1=0
⇒x=1andy=1
Thus the vertex of the parabola is A(1,1)
Also y=0⇒2x−x2=0⇒x(2−x)=0⇒x=0orx=2
Thus, the curve the x-axist at O(0,0)andB(2,0)
The rough sketch of the curve can now be drawn as shown in the given figure
∴ required area=2∫0ydx
=2∫0(2x−x2)dx=[x2−x33]20
=(4−83)=43 sq units
Hence the required area is 43 sq units .

Curve Tracing
The approximate shape of curve is obtained my following steps:
( I ) SYMMETRY
( a )Symmetry about x-axis
If the equation of curve remains unchanged by changing y by −y , then the curve is symmetrical about x-axis
E.g. y2=4ax
( b ) Symmetry about y-axis
If the equation of curve remains unchanged by changing x by −x , then the curve is symmetrical about y-axis
E.g x2=4ay
( c )Symmetry about both axes
If the equation of curve remains unchanged by changing x by −x and y by −y , then the curve is symmetrical about both xandy axis
( d )Symmetry about both axes
If the equation of curve remains unchanged by interchanging x and y , then the curve is symmetrical about y=x
E.g x4+y4=xy
( II ) Find the points on the curve crosses the x and y axis.
( III ) Find dydx and find points where f(x) us increasing or decreasing. Also find stationary points.
( IV ) Check y when x→∞ or x→−∞
Example 9
Area bounded by f(x)=(x−1)(x+1)x−2 x-axis and ordinates x=0 and x=32 is
Clearly, f(x) is everwhere continuous and differentiable except at x=2. The signs of f(x) for different values of x are shown in Fig. 11.

A rough sketch of the curve y=f(x) is as shown in Fig. 12.
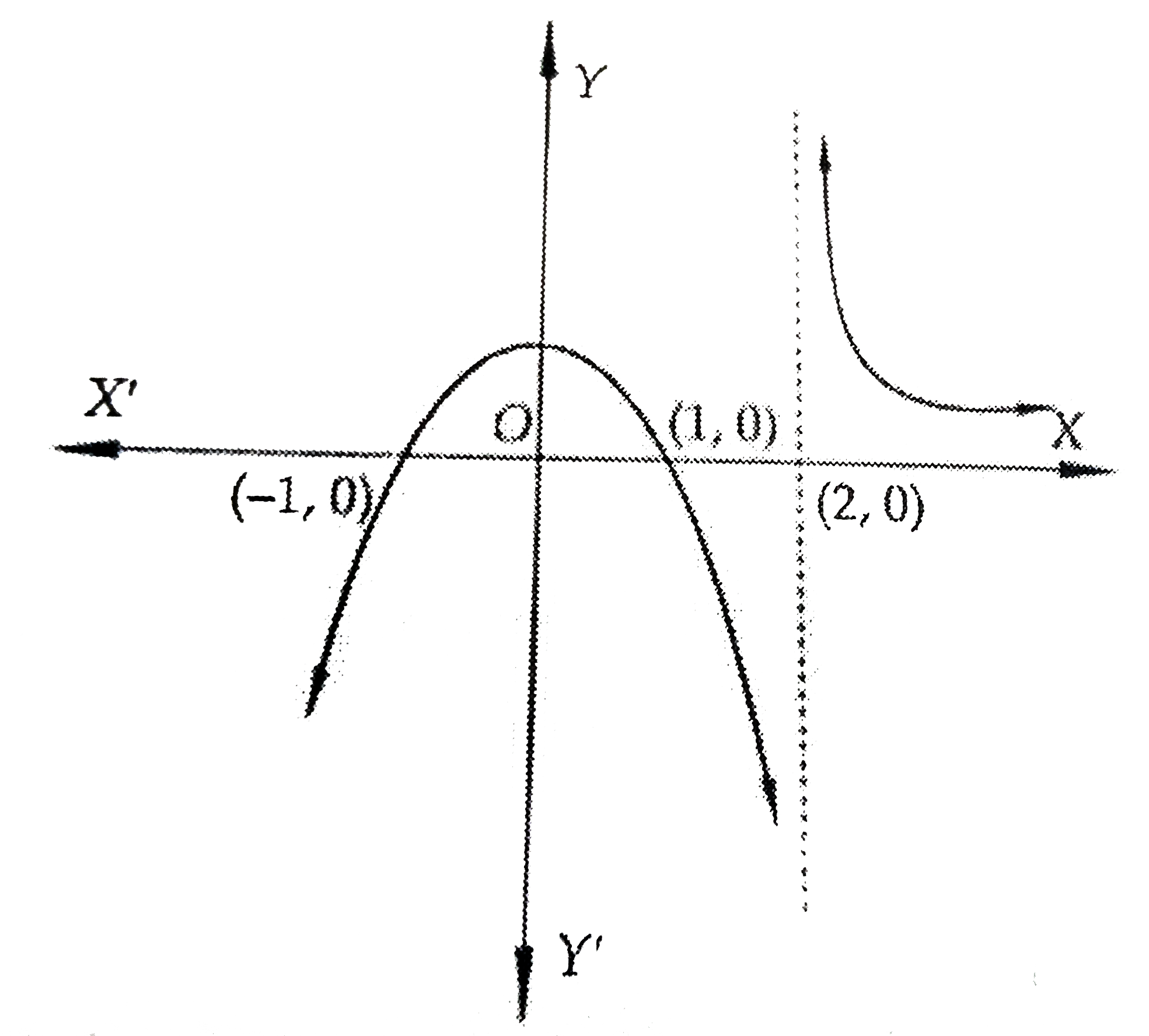
Let A denote the required area. Then,
A=3/2∫0f(x)dx
⇒A=1∫0f(x)dx+∣∣
∣
∣∣3/2∫1f(x)dx∣∣
∣
∣∣
⇒A=1∫0(x−1)(x+1)x−2dx−3/2∫1(x−1)(x+1)x−2dx
⇒A=1∫0(x+2+3x−2)dy−3/2∫1(x+2+3x−2)dx
⇒A=[(x+2)22+3log|x−2|]10−[(x−2)22+3log|x−2|]3/21
⇒A=(92−2−3log2)=[(498+log12)−92]=78 sq. units.
Example 10
Find the whole area included between the curve x2y2=a2(y2–x2) and its asymptotes
- The curve is symmetric about both the axes
- Asymptotes are x=±a
A=4∫a0ydx
=4∫a0ax√a2−x2dx
⇒4a∣∣−√a2−x2∣∣a0=4a2
Equation in Parameteric form
Let the equation of curve be in Parametric form , then A=∫βαydxdt⋅dt or ∫δγxdydt⋅dt
where α and β are corresponding values of x and y and γ and δ are corresponding values of y
Example 11
Find the area of the region bounded by an arc of the cycloid x=a(t−sint),y=a(1−cost) and the x-axis
To find the points where arc cuts x axis
a(1−cost)=0⇒t=0,π
Area =∫π0ydxdt⋅dt=∫π0a2(1−cost)2dt
a2∣∣∣(32)t−2sint+sin2t4∣∣∣π0
a2[3π2]=3πa22
Average value of a function
Average value of a function in interval a≤x≤b is given by
yavg=1b−a∫baf(x)dx
Note :
- Average value of a function can be +ve,−ve or zero
- If the function exists in (0,∞) , then,
yavg=limb→∞(1b)∫b0f(x)dx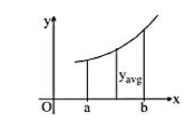
Example 12
Find the average value of the function
f(x)=cos2xsin2x+4cos2x over the interval [0,π2]. Check directly that this average, equal to 16, is the value of the function f(x) for a certain x lying within the indicated interval.
yavg=1π2−0∫π20cos2xsin2x+4cos2(4x)dx
=2π∫π201tan2x+4dx
⇒2π∫π20sec2xsec2x(tan2x+4)dx
2π∫π20sec2xdx(1+tan2x)(4+tan2x) [Substitutetanx=t]
yavg=2π∫∞0dtt2+1(4+t2)
23π[tan−1t−(12)tan−1(t2)]∞0=16
Area bounded by Inverse
The area bounded by a curve & an axis is equal to the area bounded by the inverse of that curve & the other axis, i.e., the area bounded by y = ƒ (x) and x-axis (say) is equal to the area bounded by y=ƒ−1(x)andy-axis.
Example 13
The area bounded by the curve f(x)=x+sinx and its inverse function between the ordinates x=0 and x=2π is
(A) 4π square units
(B) 8π square units
(C) 4 square units
(D) 8 square units
D
Clearly, f:[0,2π]∈[0,2π]given by f(x)=x+sinx is bijection. So its inverse exists. The graph of f−1(x) is the mirror image of the graph of f(x) in the line y=x.

∴ Required area A is given by
A=4 (Area of one loop)
⇒A=4⎡⎢⎣π∫0(x+sinx)dx−π∫0xdy⎤⎥⎦
⇒A=4π∫0sinxdx=−4[cosx]π0
⇒A=−4[cosπ−cos0]=8 sq. units.
Greatest and least value of Variable area
If y=f(x) is a monotonic function (a,b) then the area bounded by the ordinates x=a,x=b,y=f(x) and y=f(c) where [c∈(a,b)] is minimum when c=a+b2
Note: Let f(x) be the bijective function and g(x) be the inverse of the function , then the area bounded by y=g(x) and the ordinate at x=aandx=b is same as area bounded by y=f(x) and the abscissa at y=a and y=b as f(x) and g(x) be the mirror image w.r.t line y=x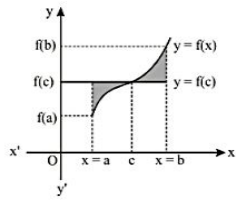
Example 14
For what value of 'a' is the area bounded by the curve y=a2x2+ax+1 and the straight line y=0. x=0andx=1 the least?
A=∫10(a2x2+ax+1)dx
A=[a2x33+ax22+x]10 {since∫xndx=xn+1n+1□}
A=[a23+a2+1]
(i)dAda=0 (ii)d2Ada2
dAda=2a3+(12)
d2Ada2=23→+ve
dAda=0
2a3+12=0⇒a=−(34)