PROBLEMS (LEVEL-II) from AAKASH SERIES CURRENT ELECTRICITY for Class 12
| Class 12 | PHYSICS |
| Chapter | CURRENT ELECTRICITY |
| AAKASH SERIES | PROBLEMS (LEVEL-II) |
| Medium | English |
| Academic Year | 2023-2024 |
Question 17
(a) In a meter bridge [Fig. 3.27], the balance point is found to be at 39.5 cm from the end A, when the resistor Y is of 12.5Ω. Determine the resistance of X. Why are the connections between resistors in a Wheatstone or meter bridge made of thick copper strips?
(b) Determine the balance point of the bridge above if X and Y are interchanged.
(c) What happens if the galvanometer and cell are interchanged at the balance point of the bridge? Would the galvanometer show any current?View SolutionQuestion 22
Two wires of equal length, one of aluminium and the other of copper have the same resistance. Which of the two wires is lighter ? Hence explain why aluminium wires are preferred for overhead power cables. (ρAl=2.63×10−8Ωm),ρCu=1.72×10−8Ωm, relative density of Al= 2.7, Cu = 8.9.)View SolutionQuestion 23
(a) Given n resistors each of resistance R, how will you combine them to get the (i) maximum (ii) minimum effective resistance? What is the ratio of the maximum to minimum resistance?
(b) Given the resistances of 1Ω,2Ω,3Ω, how will be combine them to get an equivalent resistance of (i) (11/3)Ω (ii) (11/5)Ω, (iii) 6Ω, (iv) (6/11)Ω?
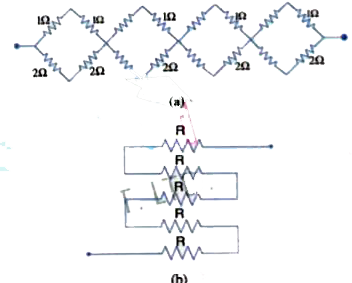
(c) Determine the equivalent resistance of networks shown in Fig. 3.31.
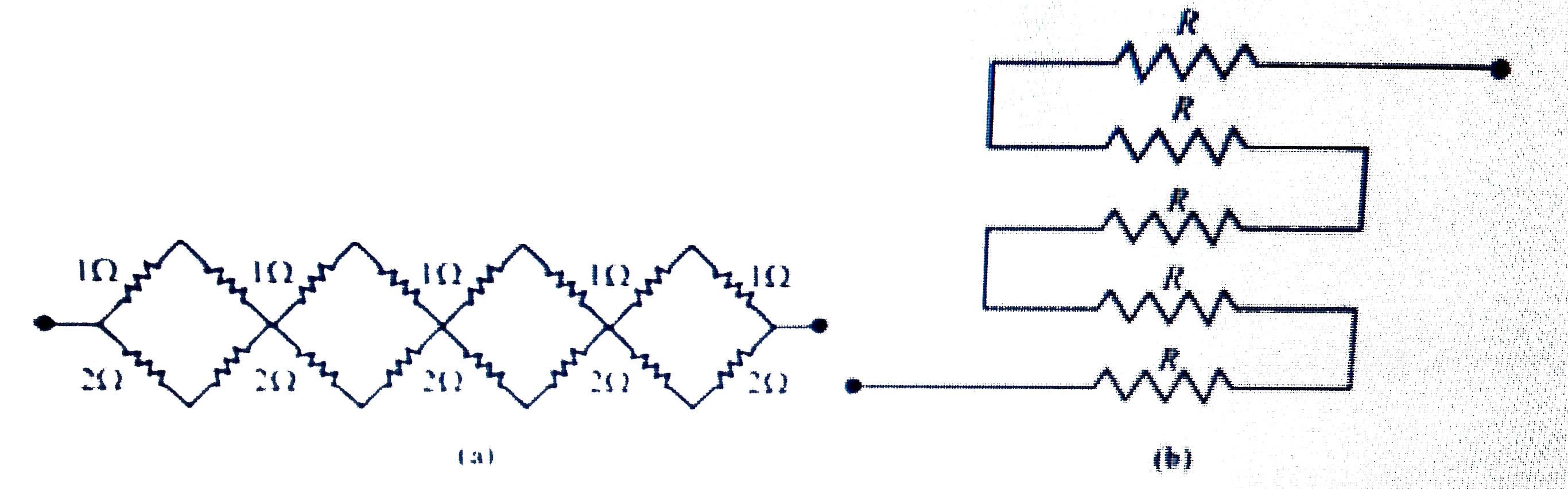 View Solution
View SolutionQuestion 29
Figure 6.13 shows a 2.0V potentiometer used for the determination of internal resistance of a 1.5V cell. The balance point of the cell in open circuit is 76.3cm. Whan a resistor of 9.5Ω is used in the external circuit of the cell, the balance point shifts to 64.8cm, length of the potentiometer. Dentermine the internal resistance of the cell.
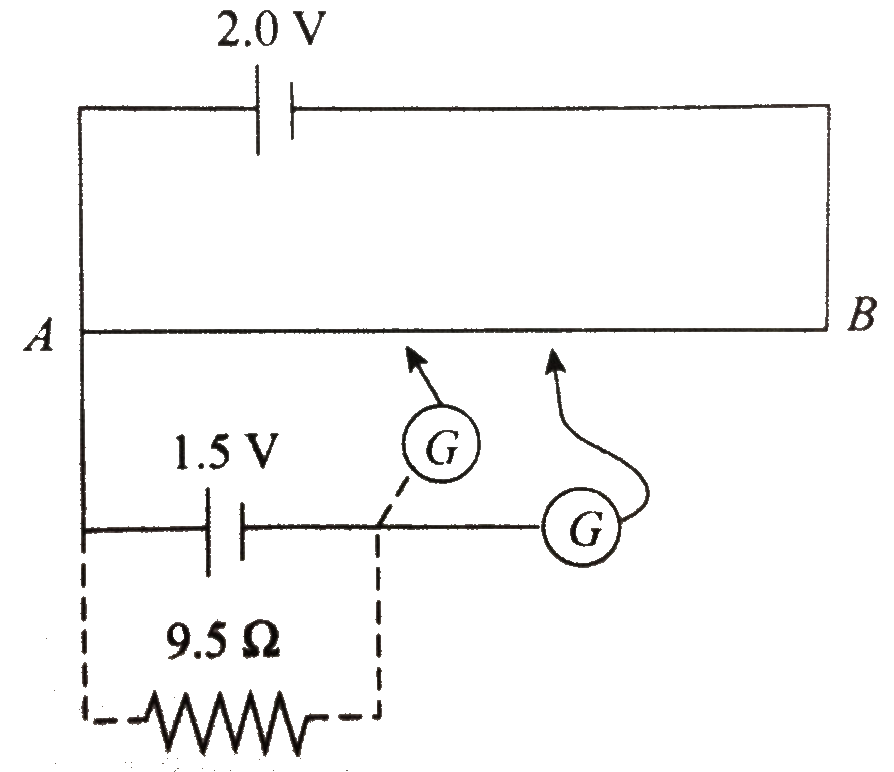 View Solution
View SolutionQuestion 30
The earth’s surface has a negative surface charge density of 10−9Cm−2. The potential difference of 400 kV between the top of the atmosphere and the surface results (due to the low conductivity of the lower atmosphere) in a current of only 1800 A over the entire globe. If there were no mechanism of sustaining atmospheric electric field, how much time (roughly) would be required to neutralise the earth’s surface? (This never happens in practice because there is a mechanism to replenish electric charges, namely the continual thunderstorms and lightning in different parts of the globe). (Radius of earth =6.37×106m.)View SolutionQuestion 34
Figure 6.36 shows a potentiometer with a cell of emf 2.0V and internal resistance 0.4Ω maintaining a potential drop across the resistor wire AB. A standard cell that maintains a constant emf of 1.02V (for very moderate current up to emf μA) gives a balance point at 67.3cm length of the wire. To ensure very low current is drawn the standard cell, a very high resistance of 600kΩ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf ε and the balance point found, similary, turns out to be at 82.3cm length of the wire.
a. What is the value of ε?
b.What purpose does the high resistance of 600kΩ have?
c. Is the balance point affected by this high resistance?
d. Is the balance point affected by internal resistance of the driver cell?
e. Would the method work in the above situation if the driver cell of the potentiometer had an emf of 1.0V instead of 2.0V?
f. Would the circuit work well for determining an extermely small emf, say of the order of a few mV (such as the typical emf of a thermocouple)? If not, how will you modify the circuit ?
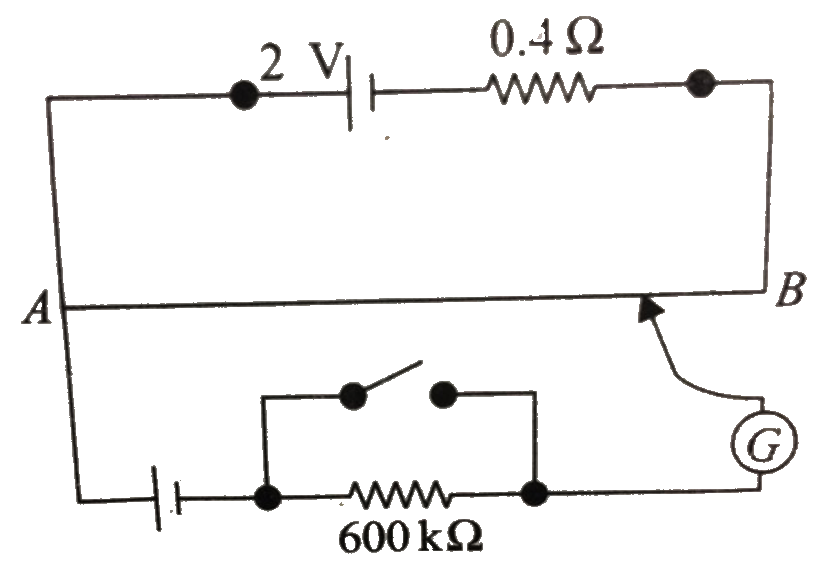 View Solution
View SolutionQuestion 35
Figure 6.36 shows a potentiometer with a cell of emf 2.0V and internal resistance 0.4Ω maintaining a potential drop across the resistor wire AB. A standard cell that maintains a constant emf of 1.02V (for very moderate current up to emf μA) gives a balance point at 67.3cm length of the wire. To ensure very low current is drawn the standard cell, a very high resistance of 600kΩ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf ε and the balance point found, similary, turns out to be at 82.3cm length of the wire.
a. What is the value of ε?
b.What purpose does the high resistance of 600kΩ have?
c. Is the balance point affected by this high resistance?
d. Is the balance point affected by internal resistance of the driver cell?
e. Would the method work in the above situation if the driver cell of the potentiometer had an emf of 1.0V instead of 2.0V?
f. Would the circuit work well for determining an extermely small emf, say of the order of a few mV (such as the typical emf of a thermocouple)? If not, how will you modify the circuit ?
 View Solution
View SolutionQuestion 36
Figure 6.36 shows a potentiometer with a cell of emf 2.0V and internal resistance 0.4Ω maintaining a potential drop across the resistor wire AB. A standard cell that maintains a constant emf of 1.02V (for very moderate current up to emf μA) gives a balance point at 67.3cm length of the wire. To ensure very low current is drawn the standard cell, a very high resistance of 600kΩ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf ε and the balance point found, similary, turns out to be at 82.3cm length of the wire.
a. What is the value of ε?
b.What purpose does the high resistance of 600kΩ have?
c. Is the balance point affected by this high resistance?
d. Is the balance point affected by internal resistance of the driver cell?
e. Would the method work in the above situation if the driver cell of the potentiometer had an emf of 1.0V instead of 2.0V?
f. Would the circuit work well for determining an extermely small emf, say of the order of a few mV (such as the typical emf of a thermocouple)? If not, how will you modify the circuit ?
 View Solution
View SolutionQuestion 37
Figure 6.36 shows a potentiometer with a cell of emf 2.0V and internal resistance 0.4Ω maintaining a potential drop across the resistor wire AB. A standard cell that maintains a constant emf of 1.02V (for very moderate current up to emf μA) gives a balance point at 67.3cm length of the wire. To ensure very low current is drawn the standard cell, a very high resistance of 600kΩ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf ε and the balance point found, similary, turns out to be at 82.3cm length of the wire.
a. What is the value of ε?
b.What purpose does the high resistance of 600kΩ have?
c. Is the balance point affected by this high resistance?
d. Is the balance point affected by internal resistance of the driver cell?
e. Would the method work in the above situation if the driver cell of the potentiometer had an emf of 1.0V instead of 2.0V?
f. Would the circuit work well for determining an extermely small emf, say of the order of a few mV (such as the typical emf of a thermocouple)? If not, how will you modify the circuit ?
 View Solution
View SolutionQuestion 38
Figure shows a potentiometer with a cell of 2.0 V and internal resistance 0.40 Ω maintaining a potential drop across the resistor wire AB. A standard cell which maintains a constant emf of 1.02 V (for every moderate currents upto a few mA) gives a balance point at 67.3 cm length of the wire. To ensure very low currents drawn from the standard cell, a very high resistance of 600 Ω is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf ε and the balance point found similarly, turns out to be at 82.3 cm length of the wire.
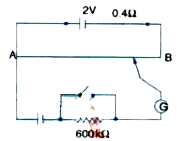
Would the method work in the above situation if the driver cell of the potentiometer had an emf of 1.0 V instead of 2.0 V? View SolutionQuestion 39
Figure shows a potentiometer with a cell of 2.0 V and internal resistance 0.40 Ω maintaining a potential drop across the resistor wire AB. A standard cell which maintains a constant emf of 1.02 V (for every moderate currents upto a few mA) gives a balance point at 67.3 cm length of the wire. To ensure very low currents drawn from the standard cell, a very high resistance of 600 Ω is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf ε and the balance point found similarly, turns out to be at 82.3 cm length of the wire.
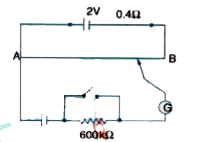
Would the circuit work well for determining an extremely small emf, say of the order of a few mV (such as the typical emf of a thermo-couple)? If not, how will you modify the circuit?View SolutionQuestion 40
Figure shows a potentiometer circuit for comparison of two resistances. The balance point with a standard resistor R= 10.0Ω is found to be 72.6 cm, while that with the unknown resistance X is 68.5 cm. Determine the value of X. What might you do if you failed to find a balance point with the given cell of emf ε ? (Take internal resistance r=1Ω)
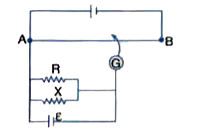 View Solution
View SolutionQuestion 43
It is desired to make a 20Ω coil of wire, which has a zero thermal coefficient of resistance. To do this, a carbon resistor of resistance R1 is placed in series with an iron resistor of resistance R2. The proportions of iron and carbon are so chosen that R1+R2=20Ω for all temperatures near 20∘C. How long are R1andR2? αcarbon=−0.5×10−3.∘C−1,αiron=5×10−3.∘C(−1) View Solution
All Exercises from AAKASH SERIES Class 12 PHYSICS CURRENT ELECTRICITY
- EXERCISE (LONG ANSWER QUESTIONS)
- EXERCISE (SHORT ANSWER QUESTIONS)
- EXERCISE (VERY ANSWER QUESTIONS)
- EXERCISE (VERY ANSWER QUESTIONS) (CHOOSE THE CORRECT ALTERNATIVE)
- EXERCISE (LONG ANSWER QUESTIONS)
- EXERCISE (SHORT ANSWER QUESTIONS)
- EXERCISE (VERY ANSWER QUESTIONS)
- EXERCISE (VERY ANSWER QUESTIONS) (CHOOSE THE CORRECT ALTERNATIVE)
- EXERCISE (LONG ANSWER QUESTIONS)
- EXERCISE (SHORT ANSWER QUESTIONS)
- EXERCISE (VERY ANSWER QUESTIONS)
- EXERCISE (VERY ANSWER QUESTIONS) (CHOOSE THE CORRECT ALTERNATIVE)
- EXERCISE (LONG ANSWER QUESTIONS)
- EXERCISE (SHORT ANSWER QUESTIONS)
- EXERCISE (VERY ANSWER QUESTIONS)
- EXERCISE (VERY ANSWER QUESTIONS) (CHOOSE THE CORRECT ALTERNATIVE)
- PROBLEMS (LEVEL-1)
- PROBLEMS (LEVEL-II)
- PROBLEMS (LEVEL-1)
- PROBLEMS (LEVEL-II)
- PROBLEMS (LEVEL-1)
- PROBLEMS (LEVEL-II)
- PROBLEMS (LEVEL-1)
- PROBLEMS (LEVEL-II)
- EXAMPLES
- EXAMPLES
- EXAMPLES
- EXAMPLES