Four resistors P.Q, R and X whose values are 2,2,2 and 3 ohms respectively are joined to form a Wheatstone Bridge. Calculate the value of resistance with which the resistance X must be shunted in order that the bridge may be balanced.
To solve the problem of finding the value of resistance with which resistance X must be shunted in order to balance the Wheatstone Bridge, we can follow these steps:
1. Identify the Resistor Values:
- The resistors are given as follows:
- P = 2 ohms
- Q = 2 ohms
- R = 2 ohms
- X = 3 ohms
2. Write the Balance Condition for Wheatstone Bridge:
- The condition for a Wheatstone Bridge to be balanced is given by the formula:
PQ=RX
3. Substitute the Known Values:
- Substitute the known values into the balance condition:
22=23
- Simplifying the left side gives:
1=23
- This shows that the bridge is not balanced.
4. Introduce a Shunt Resistance:
- Let the shunt resistance be denoted as x. When shunted, the effective resistance of X (which is 3 ohms) will be:
Reff=3x3+x
5. Set Up the New Balance Condition:
- Now, we need to set the new balance condition:
PQ=RReff
- Substituting the values gives:
22=23x3+x
- Simplifying the left side gives:
1=2(3+x)3x
6. Cross Multiply to Solve for x:
- Cross multiplying gives:
3x=2(3+x)
- Expanding the right side:
3x=6+2x
7. Rearranging the Equation:
- Rearranging the equation gives:
3x−2x=6
- Thus:
x=6 ohms
Final Answer:
The value of the shunt resistance required to balance the Wheatstone Bridge is 6 ohms.
- The resistors are given as follows:
- P = 2 ohms
- Q = 2 ohms
- R = 2 ohms
- X = 3 ohms
- The condition for a Wheatstone Bridge to be balanced is given by the formula:
PQ=RX
- Substitute the known values into the balance condition:
22=23
- Simplifying the left side gives:
1=23
- This shows that the bridge is not balanced.
- Let the shunt resistance be denoted as x. When shunted, the effective resistance of X (which is 3 ohms) will be:
Reff=3x3+x
- Now, we need to set the new balance condition:
PQ=RReff
- Substituting the values gives:
22=23x3+x
- Simplifying the left side gives:
1=2(3+x)3x
- Cross multiplying gives:
3x=2(3+x)
- Expanding the right side:
3x=6+2x
- Rearranging the equation gives:
3x−2x=6
- Thus:
x=6 ohms
The value of the shunt resistance required to balance the Wheatstone Bridge is 6 ohms.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
27 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (VERY ANSWER QUESTIONS) (Choose the correct alternative)
3 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)
16 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
2 Videos
Similar Questions
Three resistance P,Q,R each of 2Ω and an unknown resistance S from the four amrs of a Wheatstone's bridge circuit. When a resistance of 6Ω is connected in parallel to S the bridge gets balanced. What is the value of S ?
View SolutionThree resistance P,Q,R each of 2Ω and an unknown resistance S from the four amrs of a Wheatstone's bridge circuit. When a resistance of 6Ω is connected in parallel to S the bridge gets balanced. What is the value of S ?
View Solution
Knowledge Check
In a Wheatstone's network, P=2Ω,Q=2Ω,R=2ΩandS=3Ω. The resistance with which S is to be shunted in order that the bridge may be balanced is
 A1ΩB2ΩC4ΩD6Ω
A1ΩB2ΩC4ΩD6ΩFour resistances of 3Ω,3Ω,3Ωand4Ω respectively are used to form a Wheatstone bridge. The 4Ω resistance is short circuited with a resistance R in order to get bridge balanced. The value of R will be
A10ΩB11ΩC12ΩD13ΩIn a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cm
A balanced wheatstone bridge is shown the values of currents i1 and i2 are
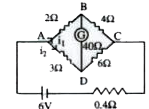
View SolutionFour resistors of 15ohm,12ohm,4ohm and 10ohm given in cyclic order to form a wheat stone bridge. What resistance (in ohm) should be connected in parallel across the 10ohm resistor to balance the wheat stone bridge

View SolutionFour resistence of 10Ω,60Ω,100Ωand 200Ω, respectively taken in order are used to form a Wheatstone's bridge . A 15 V battery is connected to the ends of a 200Ωresistance, the current through it will be
View SolutionIn Wheatstone bridge, four resistors of resistances 15Ω,12Ω,4Ω and 10Ω respectively, are connected in cyclic order. The resistance ( in Ω) that is to be connected in parallel with the resistance of 10Ω to balance the network is
View SolutionIn Wheatstone's bridge P=9ohm, Q = 11 ohm,R=4ohm and S=6ohm. How much resistance must be put in parallel to the resistance S to balance the bridge
View Solution
