Level 3 from ARIHANT PHYSICS Chapter 5 ELECTROSTATICS for Class 12
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATICS |
| ARIHANT PHYSICS | Level 3 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
Three small equally charged identical conducting balls are suspended from identical insulating threads secured at one point. Length (L) of the threads is large compared to the equilibrium separation (a) between any two balls. (a) One of the balls is suddenly discharged. Find the separation between the charged balls when equilibrium is restored. Assume that the threads do not interfere and balls do not collide. (b) If two of the balls are suddenly discharged, how will the balls behave after this? Find the separation between the balls when equilibrium is restored. The threads do not interfereView SolutionQuestion 2
Two charged particle of equal mass are constrained to move along X and Y direction. The X – Y plane is horizontal and the tracks are smooth. The particles are released from rest when they were at positions shown in the figure. At the instant distance of q becomes 2r from the origin, find the location of charge Q.
 View Solution
View SolutionQuestion 3
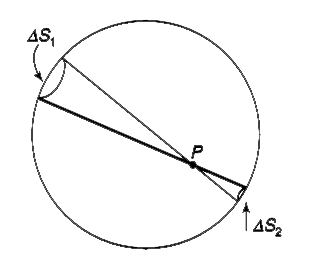
Consider a uniformly charged spherical shell. Two cones having same semi vertical angle, and their common apex at P, intercept the shell. The intercepts have area ΔS1 and ΔS2. For a cone of very small angle, ΔS1 and ΔS2 will be very small and charge on them can be regarded as point charge for the purpose of writing electric field at point P. Prove that the charge on ΔS1 and ΔS2 produce equal and opposite field at P. Hence, argue that field at all points inside the uniformly charged spherical shell is zero.
 View Solution
View SolutionQuestion 4
Two point charges +q1 and −q2 are placed at A and B respectvely. An electric line of force emerges from q1 making an angle α=60∘ with line AB and terminates as −q2 making an angle of 90∘ with line AB.
(a). Find ∣∣∣q1q2∣∣∣ ltbr> (b). Find the maximum value of angle α at which a line emitted from q1 terminates on charge q2.
 View Solution
View SolutionQuestion 6
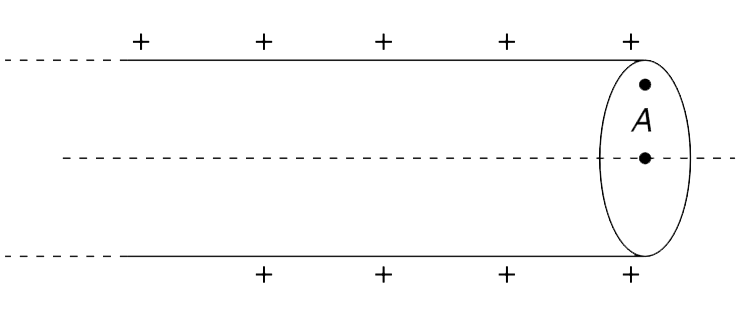
Two equal insulating threads are placed parallel to each other. Separation between the threads (= d) is much smaller than their length. Both the threads have equal and opposite linear charge density on them. The electric field at a point P, equidistant from the threads (in the plane of the threads) and located well within (see figure) is E0. Calculate the field at mid point (M) of line AB.
 View Solution
View SolutionQuestion 9
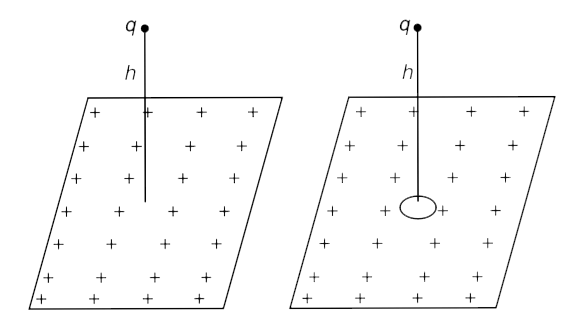
A small charged ball is in state of equilibrium at a height h above a large horizontal uniformly charged dielectric plate having surface charge density of σC/m2. (a) Find the acceleration of the ball if a disc of radius r (ltlt h) is removed from the plate directly underneath the ball. (b) Find the terminal speed (V0) acquired by the falling ball. Assume that mass of the ball is m, its radius is x and coefficient of viscosity of air is η. Neglect buoyancy and assume that the ball acquires terminal speed within a short distance of its fall.
 View Solution
View SolutionQuestion 10
In a certain region of space the electrostatic field depends only on the coordinates x and y as follows.
E=0 for √x2+y2<r0
E=a(xˆi+yˆj)(x2+y2) for √x2+y2>r0
Where a is a positive constant and ˆi and ˆj are the unit vectors along the X-and Y-axes. find the charge within a sphere of radius 2r0 with the centre at the origin.View SolutionQuestion 11
A solid sphere of radius R has total charge Q. The charge is distributed in spherically symmetric manner in the sphere. The charge density is zero at the centre and increases linearly with distance from the centre. (a) Find the charge density at distance r from the centre of the sphere. (b) Find the magnitude of electric field at a point ‘P’ inside the sphere at distance r1 from the centre.View SolutionQuestion 12
A ball of radius R carries a positive charge whose volume charge depends only on the distance r from the ball's centre as: ρ=ρ0(1−rR)
Where r0 is a constant. Take ε to be permittivit of the ball. Calculate the maximum electric field intensity at a point (inside or outside the ball) due to such a charge distribution.View SolutionQuestion 13
A frustum is cut from a right circular cone. The two circular faces have radii R and 2R and their centers are at O1 and O2 respectively. Height of the frustum is h=3R. When a point charge Q is placed at O1, the flux of electric field through the circular face of radius 2R is ϕ1 and when the charge Q is placed at O2, the flux through the other circular face is ϕ2. find the ratio ph1ϕ2
 View Solution
View SolutionQuestion 14
The electric field in a region of space varies as E=(xˆi+2yˆj)+3zˆk) V/m
(a). Consider an elemental cuboid whose one vertex is at (x,y,z) and the three sides are dx, dy and dz, sides being parallel to the three co-ordinate axes. Calculate the flux of electric field through the cube.
(b). Usig the expression obtained in (a) find the charge enclosed by a spherical surface of radius r, centred at the origin.View SolutionQuestion 15
A ball of radius R has a uniformly distributed charge Q. The surrounding space of the ball is filled with a volume charge density ρ=br , where b is a constant and r is the distance from the centre of the ball. It was found that the magnitude of electric field outside the ball is independent of distance r. (a) Find the value of Q. (b) Find the magnitude of electric field outside the ball.View SolutionQuestion 16
A uniform semicircular ring of radius R is in yz plane with its centre at the origin. The half ring carries a uniform linear charge density of λ.
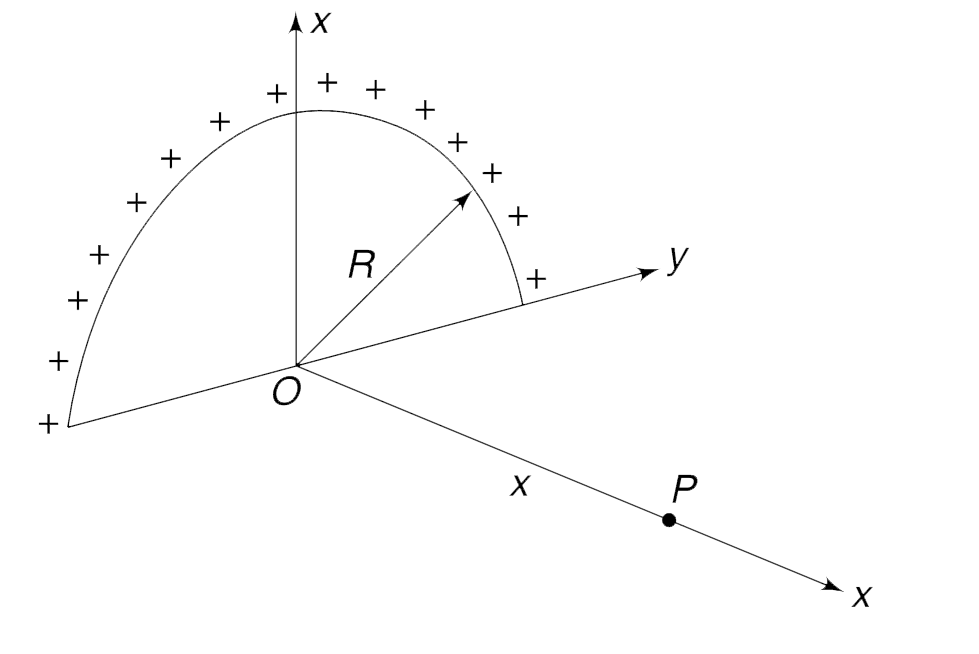
(a) Find the x, y and z component of Electric field at a point P(x, 0, 0) on the axis of the ring. (b) Prove that the field at P is directed along a line joining the centre of mass of the half ring to the point P. View SolutionQuestion 17
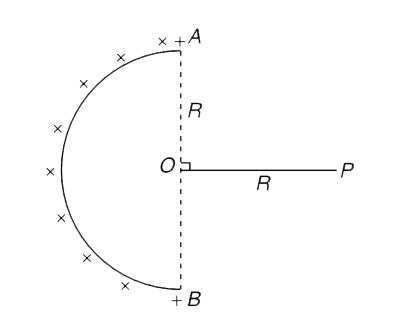
A charge – Q is placed at some distance from a neutral conductor. Charge is induced on its surface. In the neighbourhood of a point P on its surface, the charge density is σC/m2. Consider a small area ΔS on the surface of the conductor encircling point P. Find the resultant force experienced by the area ΔS due to charge present on the surface elsewhere and the charge – Q.
 View Solution
View SolutionQuestion 18
A soap bubble of radius R = 1 cm is charged with the maximum charge for which breakdown of air on its surface does not occur. Calculate the electrostatic pressure on the surface of the bubble. It is know that dielectric breakdown of air takes place when electric field becomes larger then E0=3×106W/mView SolutionQuestion 19
A conducting sphere of radius R is cut into two equal halves which are held pressed together by a stiff spring inside the sphere. (a) Find the change in tension in the spring if the sphere is given a charge Q. (b) Find the change in tension in the spring corresponding to the maximum charge that can be placed on the sphere if dielectric breakdown strength of air surrounding the sphere is E0. View SolutionQuestion 20
Surface tension of a soap solution is T. There is a soap bubble of radius r. Calculate the amount of charge that must be spread uniformly on its surface so that its radius becomes 2r. Atmospheric pressure is P0. Assume that air temperature inside the bubble remains constant. View SolutionQuestion 21
A point charge Q has been placed at a point outside a neutral spherical conductor. The induced charge density at point P on the surface of the conductor is −σ The distance of point P from the point charge Q is 2R (where R is radius of the conductor). Find the magnitude and direction of electric field at a point outside the conductor that is very close to its surface near P. View SolutionQuestion 22
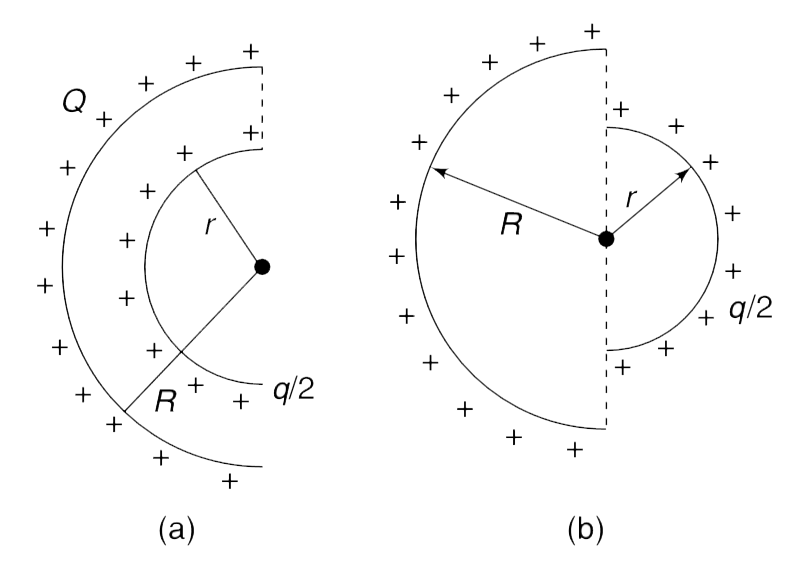
A spherical shell of radius r carries a uniformly distributed surface charge q on it. A hemispherical shell of radius R(gt r) is placed covering it with its centre coinciding with that of the sphere of radius r. The hemisphere has a uniform surface charge Q on it. The charge distribution on the sphere and the hemisphere is not affected due to each other. Calculate the force that the sphere will exert on the hemisphere.
 View Solution
View SolutionQuestion 24
A charged ball with mass m and charge q is dropped from a height h over a non-conducting smooth horizontal plane. There exists a uniform electric field E0 in vertically downward direction and the coefficient of restitution between the ball and the plane is e. Find the maximum height attained by the ball after nth collision.View SolutionQuestion 25
In the last question, the electric field in vertical direction is switched off and a field of same strength(E0) is switched on in horizontal direction. Find the horizontal velocity of the ball during the nth collision. Also calculate the time interval between nth and (n+1)th collisionView SolutionQuestion 26
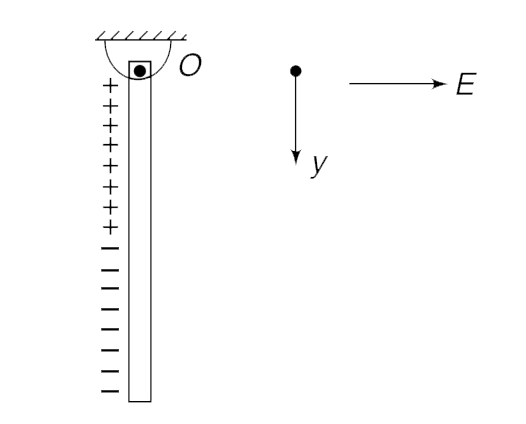
A thin insulating rod of mass m and length L is hinged at its upper end (O) so that it can freely rotate in vertical plane. The linear charge density on the rod varies with distance (y) measured from upper end as
λ=ay20≤y≤L2=−bynL2<y≤L⎫⎬⎭
Where a and b both are positive constants. whena horizontal electric field E is switched on the rod is found to remains stationary.
(a). find the value of constant b in terms of a. Also find n.
(b). Find the force applied by the hinge on the rod, if EaL3=45mg.
 View Solution
View SolutionQuestion 27
Two charges −2Q abd Q are located at the points with coordinates (−3a,0) and (+3a,0) respectively in the x-y plane. (i) Show that all points in the x-y plane where the electric potential due to the charges is zero, on a circle. Find its radius and the location of its centre (ii) Give the expression V(x) at a general point on the x-axis and sketch the function V(x) on the whole x-axis. (iii) If a particle of charge +q starts from rest at the centre of the circle, shown by a short quantitative argument that the particle eventually crosses the circule. Find its speed when it does so.View SolutionQuestion 28
A metallic sphere of radius R has a small bulge of hemispherical shape on its surface. The radius of the bulge is r. If a charge Q is given to the sphere, calculate the quantity of charge on the surface of the bulge. Assume that charge is uniformly distributed on the surface of the bulge (though it is wrong !) and also on the remaining surface of the sphere. View SolutionQuestion 32
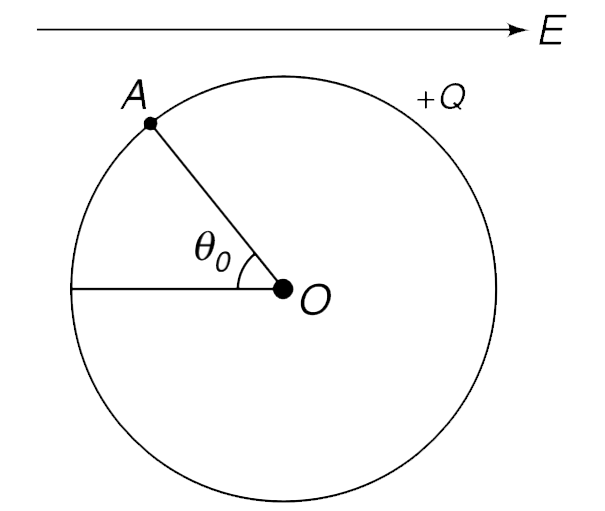
A conducting sphere of radius R having charge Q is placed in a uniform external field E. O is the centre of the sphere and A is a point on the sphere of the sphere such that AO makes an angle of θ0=60∘ with the opposite direction fo external field. calculate the potential at point A due to charge on the sphere only.
 View Solution
View SolutionQuestion 33
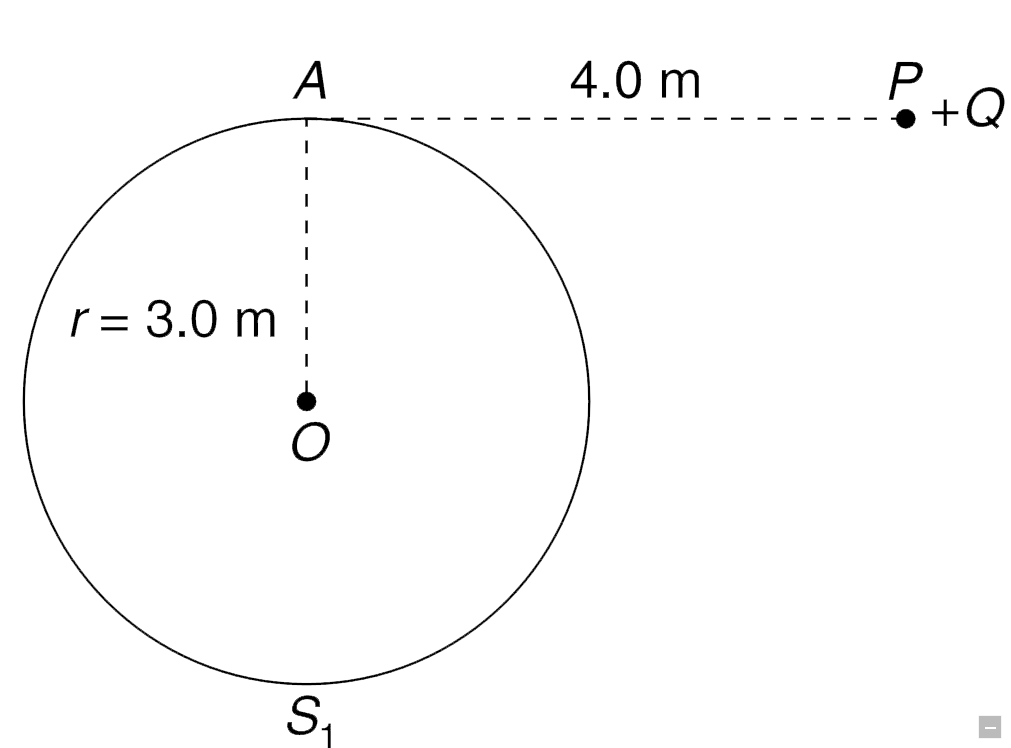
Consider a solid neutral conducting sphere S1 of radius r=3.0m. A point charge Q=+2μC s placed at point P such that AP=-4.0m (AP is tangent to the sphere). Charge Q' is induced on the surface of te conducting sphere S1. Consider another non conducting sphere (S2) of same radius r. Charge Q' is spread on the surfaec of S2 in exactly the same way as it is present on the surface of conducting sphere S1 [i.e., the distribution of charge on surface of S2 is exact replica of the induced surface charge on S1]. There is no other charge in vicinity of S2. Find the smallest potential (at a point) on the surface of sphere S2.
 View Solution
View SolutionQuestion 34
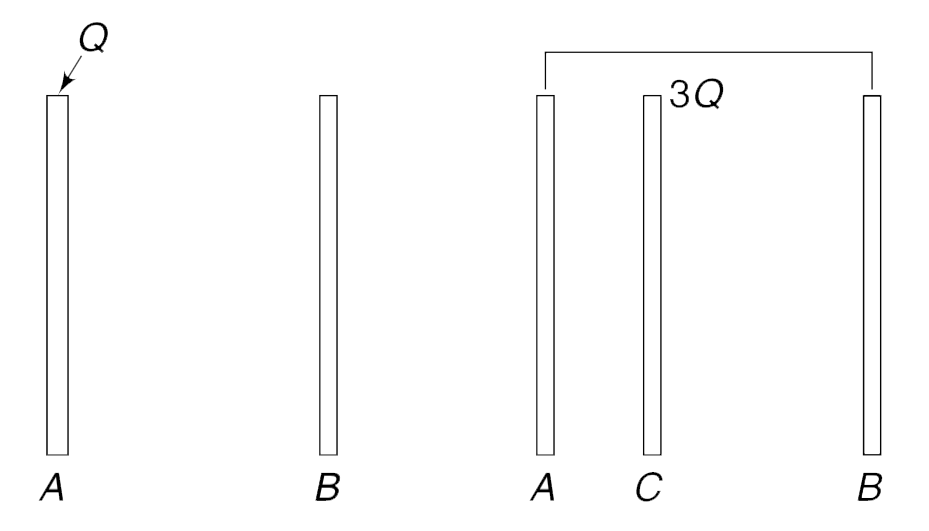
A and B are two large identical thin metal plates placed parallel to each other at a small separation. Plate A is given a charge Q. (i) Find the amount of charge on each of the two faces of A and B. (ii) Another identical plate C having charge 3Q is inserted between plate A and B such that distance of C from B is twice its distance from A. Plate A and B is shorted using a conducting wire. Find charge on all six faces of plates A, B and C. (iii) In the situation described in (ii) the plate A is grounded. Now write the charge on all six faces.
 View Solution
View SolutionQuestion 35
The figure shows equipotential surfaces due to two poit charges +3Q and -Q placed at a separation d.
(a) Will the shape of epuipotential surface be spherical very close to both the point charges? What shape of equipotentials will be seen at very far away points from the pair of charges. (b) Find the distance of point P from the negative charge. (c) Find the potential of the surface marked as S1 is the figure. (d) Consider the surface having zero potential. Write the flux of electric field through this surface
 View Solution
View SolutionQuestion 36
Three point charge have been placed along the x axis at points A, B and C. Distance AB = BC. The field lines generated by the system is shown in figure. (a) Plot the variation of electric potential along x axis. Show potential on y axis of your graph. (b) Plot the variation of electric potential along y axis with B as origin. Shows potential on x axis in your graph.
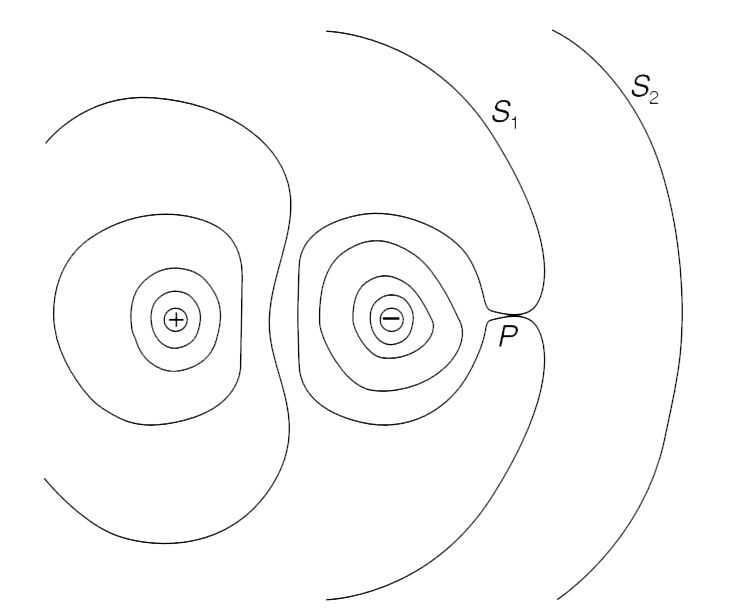 View Solution
View SolutionQuestion 37
A conducting shell has inner radius R and outer radius 2R. A charge + q is given to the spherical shell. (a) Find the electric field at a point which is at a distance x from the centre of the shell. Give your answer for three cases (i) x lt R (ii) R lt x lt 2R (iii) x gt 2R (b) Find the electric potential in all the three cases mentioned in (a) (c) Find field and potential in all the three cases mentioned in (a) after a point charge – q is introduced at the centre of the shell. (d) Write the electrical potential energy of the system consisting of the shell and the point charge at its centre. (e) Find the electrostatic force that the shell exerts on the point charge. (f) Now, another point charge + q is placed at a distance 4R from the centre of the shell. Find electric field and potential in following cases. (i) x lt R (ii) R lt x lt 2R
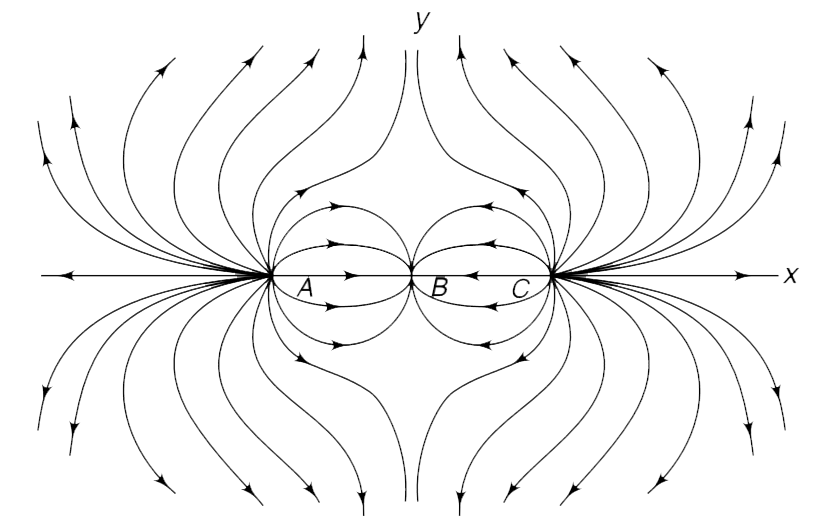 View Solution
View SolutionQuestion 38
A solid conducting sphere of radius R is surrounded by a concentric metallic shell of inner radius 2R and outer radius 3R. The shell is earthed. The inner sphere is connected to a switch S by a thin conducting wire through a small hole in the shell. By closing the switch S, the inner sphere is connected to a distant conducting sphere of radius R having charge Q. Find the charge that flows to earth through wire AB.
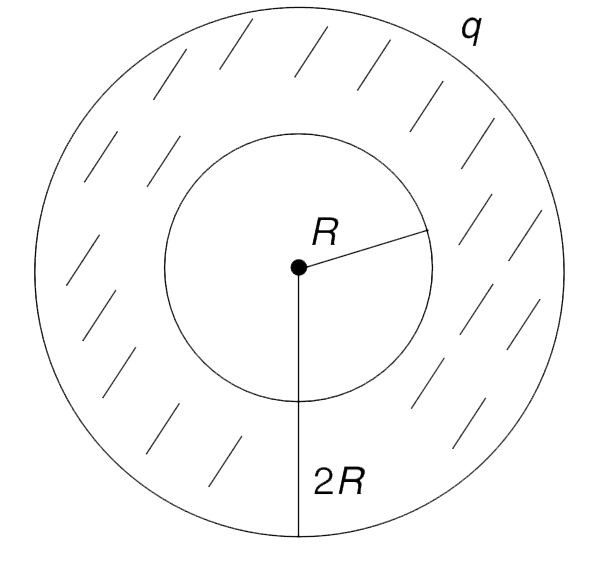 View Solution
View SolutionQuestion 39
A solid conducting sphere of radius R is surrounded by a concentric metallic shell of inner radius 2R and outer radius 3R. The shell is earthed. The inner sphere is connected to a switch S by a thin conducting wire through a small hole in the shell. By closing the switch S, the inner sphere is connected to a distant conducting sphere of radius R having charge Q. Find the charge that flows to earth through wire AB.
 View Solution
View SolutionQuestion 40
Two small identical conducting balls each of radius r and mass m are placed on a frictionless horizontal table, connected by a light conducting spring of force constant K and un-deformed length L (L gtgt r). A uniform electric field of strength E is switched on in horizontal direction parallel to the spring. (a) How much charge will appear on the two balls when they are at separation L. (b) The system fails to oscillate if K lt K0. Find K0. (c) Assuming K=2K0, find the time period of oscillation after the electric field is switched on.
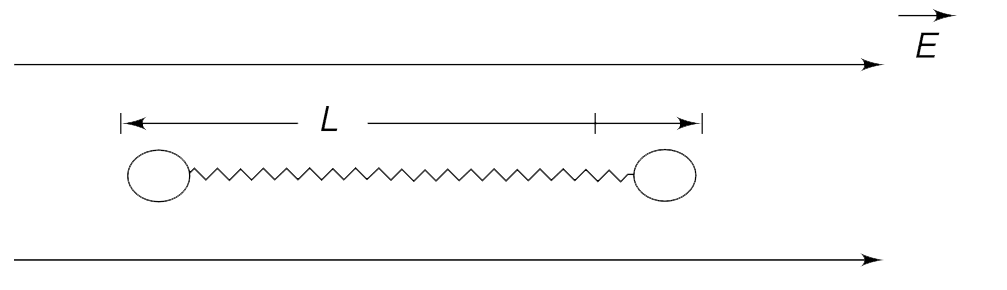 View Solution
View SolutionQuestion 41
Four charges have equal magnitude. Two of them are positive and remaining two are negative. Charges have been placed on the vertices of a rectangle and the electrostatic potential energy of the system happens to be zero. (a) Show the arrangement of the charges on the vertices of the rectangle. (b) If the smaller side of the rectangle has a length of 1.0 m, show that length of larger side must be less than 2.0 m. [Actually you need to solve on algebraic polynomial to get the exact length of the larger side. Here I am not exactly interested in making you solve that equation] View SolutionQuestion 42
On a horizontal table, there is a smooth circular groove of mean radius R. The walls of the groove are non conducting. Two metal balls (each having mass m and radius r) are placed inside the groove with their centers R apart. The balls just fit inside the groove. The two balls are given charge + 3q and – q and released from state of rest. Ignore the non-uniformity in charge distribution as the balls come close together and collide. The collision is elastic. Find maximum speed acquired by each ball after they collide for the first time.
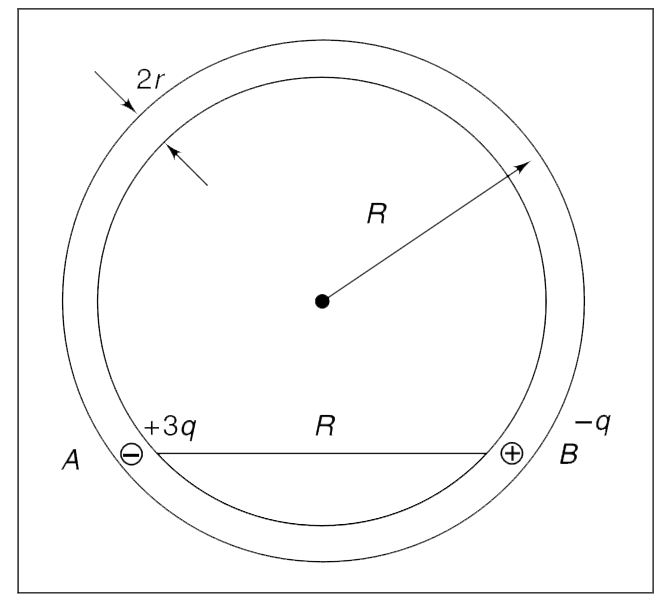 View Solution
View SolutionQuestion 43
A particle having charge Q and mass M = 2 m is tied to two identical particles, each having mass m and charge q. The strings are of equal length, l each, and they are inextensible. The system is held at rest on a smooth horizontal surface (with string taut) in a position where the strings make an angle of 60∘ between them. From this position the system is released. (a) Find the amplitude of oscillation of M (b) Find maximum speed acquired by M (c) Find tension in the string when all the three particles get in one straight line.
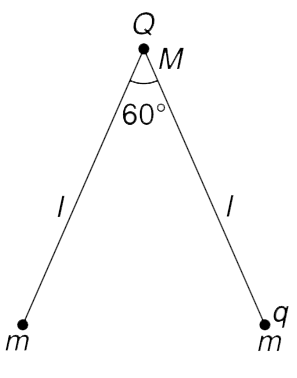 View Solution
View SolutionQuestion 44
Four point charges +8μC,−1μC,−1μC and , +8μC are fixed at the points −√27/2m,−√3/2m,+√3/2m
and +√27/2m respectively on the y-axis. A particle of mass 6×10−4kg and +0.1μC moves along the x-direction. Its speed at x=+∞ is v0. find the least value of v0 for which the particle will cross the origin. find also the kinetic energy of the particle at the origin in tyhis case. Assume that there is no force part from electrostatic force.View SolutionQuestion 45
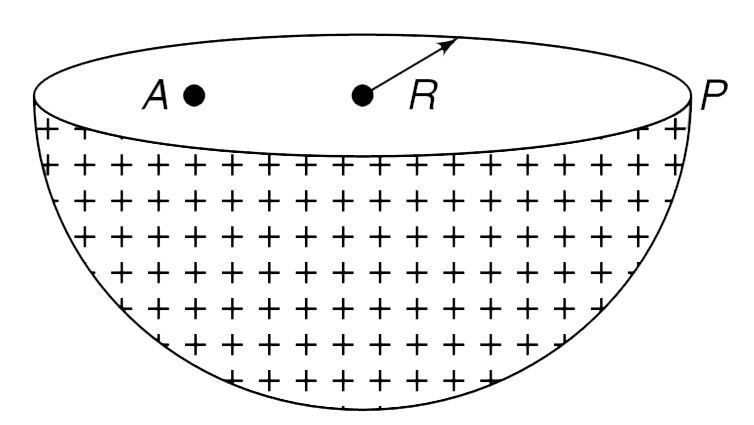
A dielectric disc of radius R and uniform positive surface charge density σ is placed on the grup with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disc from a height H with dropped, along the axis of the disc from a height H with zero intial velocity. The charge -mass ratio of the particle is qm=4εon0gσ.
(i). Find the value of H if the particle just reaches the disc.
(ii). Sketch the potential energy of the particle as a function of its height and find its height in equilibrium position.View SolutionQuestion 46
An infinite line cahrge is perpendicular to the plane of the figure having linear charge density λ, A partcle having charge Q and mass m is projected in the field of the line cahrge fromo point P. the point P is at a distance R from the line cahrge and velocity given tot he particle is perpendicular tot he radial line at P (see figure)
(i). Find the speed of the particle when its distance from the line cahrge grows the ηR(η>1)
(ii). Find the velocity component of the particle along the radial line (joining the line charge to the particle) at the instant its distance becomes ηR.
 View Solution
View SolutionQuestion 47
A uniformly charged non conducting rod is suspended vertically at its end. The rod can swing freely in the vertical plane without any friction. The linear charge density on the rod is λC/m and it has a uniformly distributed mass of M
Length of the rod is L. A uniform horizontal electrif field (E) is switched on in the region.
(a). For what value of electric field (call it E0) the rod just manages to make itself horizontal.?
(b). If eletrif field E0 is switched on, what is the maximum angular speed acquired by the rod during its motion?
 View Solution
View SolutionQuestion 48
In the last question let us assume that the uniform electric field makes an angle θ with the vertical in downward direction. With the uniformly charged rod in vertical position the field is switched on. Mass of the rod, its length and charge per unit length is M, L and λ respectively. (a) Find the strength of field (E) such that the rod can reach the horizontal position if θ=30∘ (b) Find the minimum strength of field (E) such that the rod can reach the horizontal position if θ=60∘ (c) However high the field might be, the rod cannot become horizontal if θ<θ0 find θ0
 View Solution
View SolutionQuestion 49
A massless rod of length L has two equal charges (q) tied to its ends. The rod is free to rotate in horizontal plane about a vertical axis passing through a point at a distance L4 from one of its ends. A uniform horizontal electric field (E) exists in the region. (a) Draw diagrams showing the stable and unstable equilibrium positions of the rod in the field. (b) Calculate the change in electric potential energy of the rod when it is rotated by an angle Δθ from its stable equilibrium position. (c) Calculate the time period of small oscillations of the rod about its stable equilibrium position. Take the mass of each charge to be m. View SolutionQuestion 50
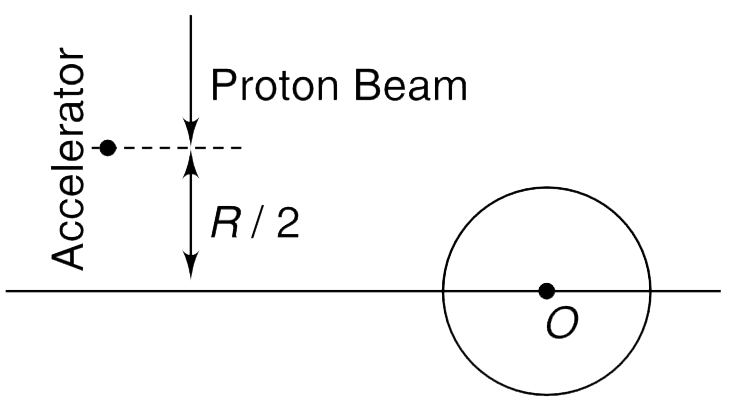
A proton accelerator produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharged distant metal sphere of radius R. The sphere is fixed and centered at point O. The initial path of the beam is at a distance of (R/2) from the centre, as indicated in the diagram. The protons in the beam that collide with the sphere get absorbed and cause it to become uniformly charged. The subsequent potential field at the accelerator due to the sphere can be neglected. Assume the mass of the proton as mP and the charge on it as e.
(a) After a long time, when the potential of the sphere reaches a constant value, sketch the trajectory of proton in the beam. (b) Once the potential of the sphere has reached its final, constant value, find the minimum speed v of a proton along its trajectory path. (c) Find the limiting electric potential of the sphere. View SolutionQuestion 51
Consider a uniformly charged spherical shell of radius R having charge Q charge Q can be through to be made up of number of point charges q1,q2,q3... etc. the electrostatic energy of the charged shell is sum of interaction energies of all possible pairs of charges.
U=∑qiqj4πε0rij
Where rij is distance between qi and qj. for continuous charg on the shell, the summation has to be carried through intergration.
(a). Calculate the electrostatic energy of the shell. We can term this energy as self energy of the shell.
(b). Calculate the work done in assembling a spherical shell of uniform charge Q and radius R by bringing charges in small installments from infinity and putting them of the shell. Do you ding the answers in (a) and (b) to be same?View SolutionQuestion 52

(a). Use the method in part (b) of the previous problem of calculate the electrostatic self energy of a uniformly charegd sphere of radius R having charge Q.
(b). Divide the above sphere (mentally) into two regions-spherical concentric part having radius R2 and the remaining annular part (between R2 and R). Denote the point charges in sphere of radius R/2 by q1,q2,q3 .. . .etc.
The charges in annular part be denoted by Q1,Q2,Q3 . . . etc.
Calculate the electrostatic interaction energy for all pairs like [(Qi,Qj)+(qi+qj)].View SolutionQuestion 53
A conducting sphere S1 of radius r is attached to an insulating handle. Another conduction sphere S2 of radius R is mounted on an insulating stand. S2 is initially uncharged. S1 is given a charge Q brought into contact with S2 and removed. S1 is recharge such that the charge on it is again Q and it is again brought into contact with S2 and removed. This procedure is repeated n times.
a. Find the electrostatic energy of S2 after n such contacts with S1.
b. What is the limiting value of this energy as n→∞ ?View SolutionQuestion 54
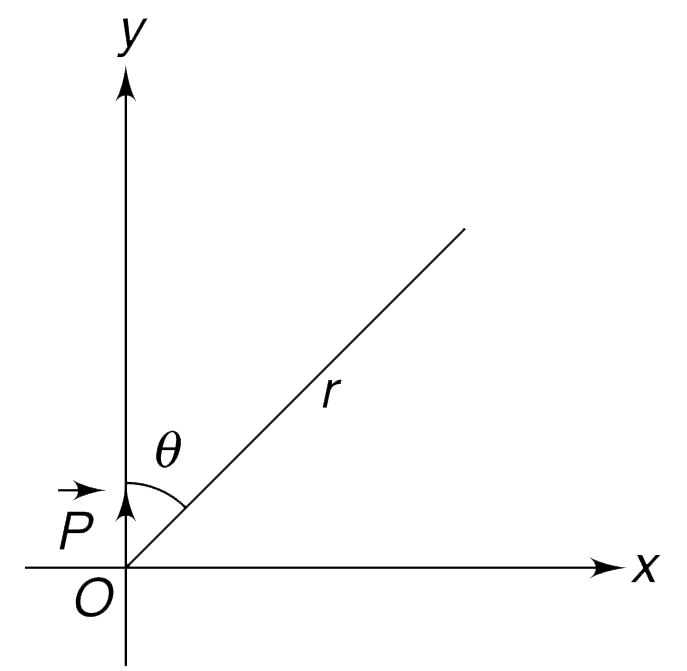
A short electric dipole is placed at the origin of the Co-ordinate system with its dipole moment P along y direction. Give answer to following questions for points which are at large distance r from the origini in x-y plane.
[r is large compared to length of the dipole]
(a). Find maximum value of x component of electric field at a piont that is at r0 distance from the origin
(b). Prove that (for 0<θ<90∘) all the points, where electric field due to the di8pole is parallel to x-axis, fall on a straight line, find the slope of the line.View SolutionQuestion 55
A tri atomic molecule X2Y has plane structure as shown in figure. Due to difference in electronegativity, charge acquired by each X atom is q and charge on Y atom is – 2q. The bond length between Y and X is d, and angle between the two bonds is θ=120∘ mass of one atom of X and Y are m and 8m respectively. The molecule is placed in a uniform Electric field E and is making small oscillations about an axis perpendicular to the plane of figure and passing through the centre of mass of the molecule. Find the time period of oscillation.
 View Solution
View SolutionQuestion 56
A short electric dipole (dipole moment P) is placed on the axis of a uniformly charged ring at a distance x from the centre as shown in figure. Radius of the ring is a and charge on it is Q.
Write the force on the dipole when x=a2 and when x=a. why the direction of force at two points is different?
(ii) is the force ont he dipole zero if x=0 ? if not where will you place the dipole so that force on it is zero.
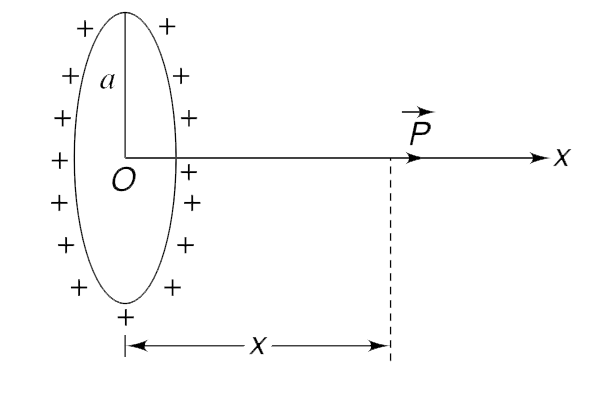 View Solution
View SolutionQuestion 57
Consider two spheres of the same radius R having uniformly distributed volume charge density of same magnitude but opposite sign (+ρ and −ρ) the spheres overlap such that the vector joining the centre of the negative sphere to that of the positive sphere is →d. (d<<R). Find magnitude of electric field at a point outside the spheres at a distance r in a direction making an angle θ with →d. Distance r is measure with respect to the mid point of the line joining the centers of the two spheres.View SolutionQuestion 58
A small, electrically charged bead can slide on a circular, frictionless, thin, insulating ring. Charge on the bead is Q and its mass is m . A small electric dipole, having dipole moment P is fixed at the centre of the circle with the dipole’s axis lying in the plane of the circle. Initially, the bead is held on the perpendicular bisector of the dipole (see fig.) Ignore gravity and answer the following questions.
(a) Write the speed of the bead when it reaches the position θ shown in the figure. (b) Find the normal force exerted by the ring on the bead at position θ. (c) How does the bead move after it is released? Where will the bead first stop after being released? (d) How would the bead move in the absence of the ring?
 View Solution
View Solution