Level 2 from ARIHANT PHYSICS Chapter 5 ELECTROSTATICS for Class 12
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATICS |
| ARIHANT PHYSICS | Level 2 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
Two unequal masses, m1=2m and m2=m have unequal positive charge on them. They are suspended by two mass-less threads of unequal lengths from a common point such that, in equilibrium, both the masses are on same horizontal level. The angle between the two strings is θ=45∘ in this position. Find the Electrostatic force applied by m1 on m2 in this position.
 View Solution
View SolutionQuestion 2
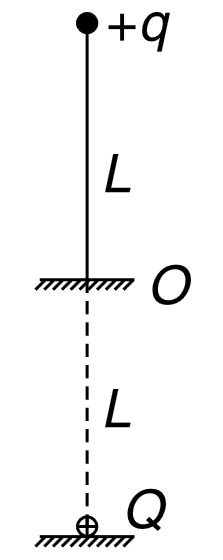
A particle of mass m and charge q is attached to a light insulating thread of length L. The other end of the thread is secured at point O. Exactly below point O, there is a small ball having charge Q fixed on an insulating horizontal surface. The particle remains in equilibrium vertically above the ball with the string taut. Distance of the ball from point O is L. Find the minimum value of Q for which the particle will be in a stable equilibrium for any gentle horizontal push given to it.
 View Solution
View SolutionQuestion 4
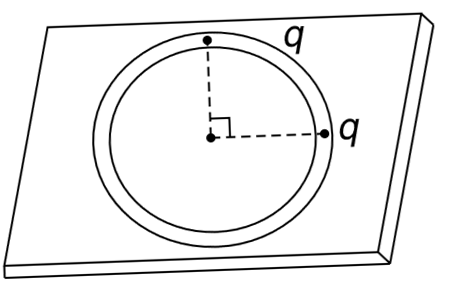
A horizontal circular groove is made in a wooden board. Two positive charges (q each) are placed in the groove at a separation of 90∘ (see figure). Where shall we place (in the groove) a third charge and what shall be its magnitude such that all three of them remain at rest after they are released. Answer for two cases: (a) When the third charge is positive. (b) When the third charge is negative. Neglect friction and assume that the groove is very thin just wide enough to accommodate the particles. [Take sin22.5∘=0.38,cos22.5∘=0.92]
 View Solution
View SolutionQuestion 5
Two identical positive charges Q each are placed on the x axis at point (-a,0) and (a,0) A point charge of magnitude q is placed at the origin. For small displacement along x axis, the charge q executes simple harmonic motion if it is poitive and its time period is T1. if the charge q is negative, it perform oscillations when displaced along y axis. in this case the time period of small oscillations is T2. find T1T2View SolutionQuestion 6
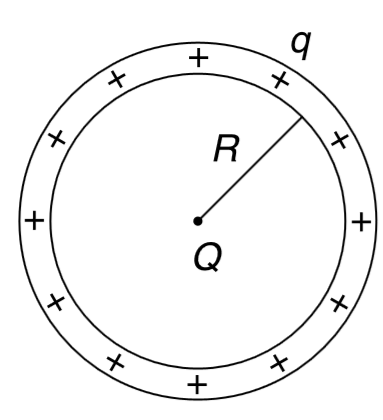
A ring of radius R has uniformly distributed charge q. A point charge Q is placed at the centre of the ring. (a) Find the increase in tension in the ring after the point charge is placed at its centre. (b) Find the increase in force between the two semicircular parts of the ring after the point charge is placed at the centre. (c) Using the result found in part (b) find the force that the point charge exerts on one half of the ring.
 View Solution
View SolutionQuestion 8
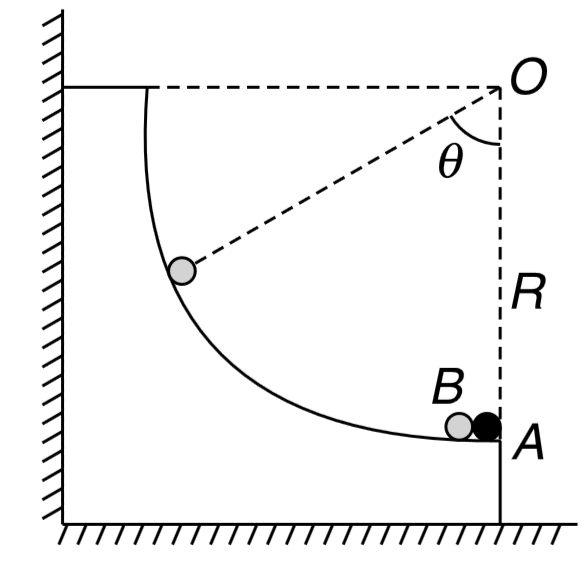
A fixed non conducting smooth track is in the shape of a quarter circle of radius R in vertical plane. A small metal ball A is fixed at the bottom of the track. Another identical ball B, which is free to move, is placed in contact with ball A. A charge Q is given to ball A which gets equally shared by the two balls. Ball B gets repelled and ultimately comes to rest in its equilibrium position where its radius vector makes an angle θ(θ<90∘) with vertical. Mass of ball is m. Find charge Q that was given to the balls.
 View Solution
View SolutionQuestion 9
A smooth fixed rod is inclined at an angle θ to the horizontal. At the bottom end of the rod there is a fixed charge +Q. There is a bead of mas m having charge q that can slide freely on the rod. The equilibrium separation of the bead from fixed charge Q is x0 Find the frequency of oscillation of the bead if it is displaced a little from its equilibrium position.
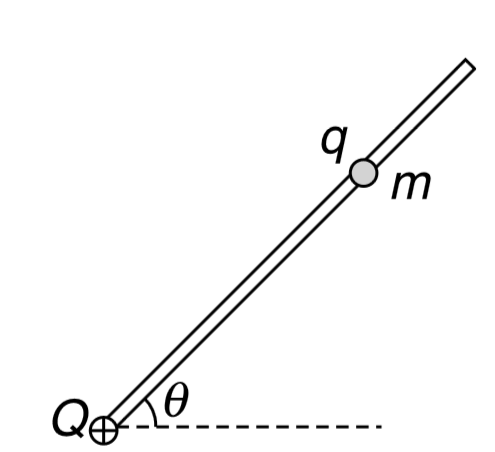 View Solution
View SolutionQuestion 10
Two charges, Q each, are fixed on a horizontal surface at separation 2a. Line OY is vertical and is perpendicular bisector of the line joining the two charges. Another particle of mass m and charge q has two equilibrium positions on the line OY, at A and B. The distances OA and OB are in the ratio 1:3√3 (a) Find the distance of the point on the line OY where the particle will be in stable equilibrium. (b) Where will the particle experience maximum electric force – at a point above B or at a point between A and B or somewhere between O and A? Where is the acceleration of particle maximum on y axis from O to B?
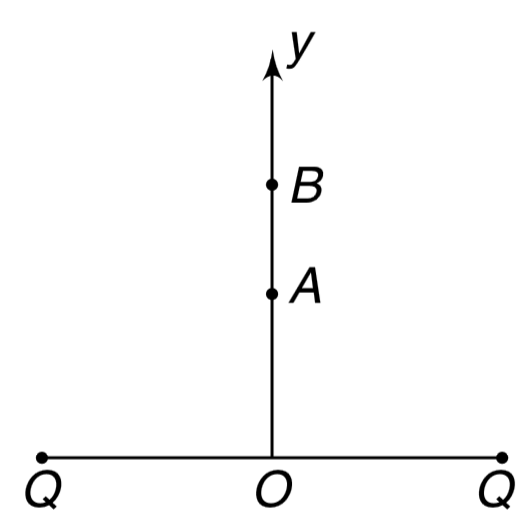 View Solution
View SolutionQuestion 11
A neutral spherical conductor has a cavity. A point charge q is located inside it. It is in equilibrium. An external electric field (E) is switched on that is directed parallel to the line joining the centre of the sphere to the point charge. (a) What is the direction of acceleration of the charge particle inside the cavity after E is switched on. (b) How is the induced charge on the wall of the cavity affected due to the external field.
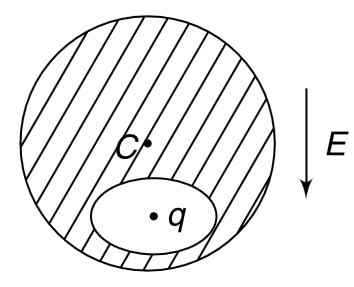 View Solution
View SolutionQuestion 17
There is an infinite non conducting sheet of charge having uniform charge density σ. The electric field at a point P at a distance x from the sheet is E0. Point O is the foot of the perpendicular drawn from point P on the sheet. A circular portio of radius r<<x centered at O is removed from the sheet. Now the field at point P becomes E0−ΔE. Find ΔE.
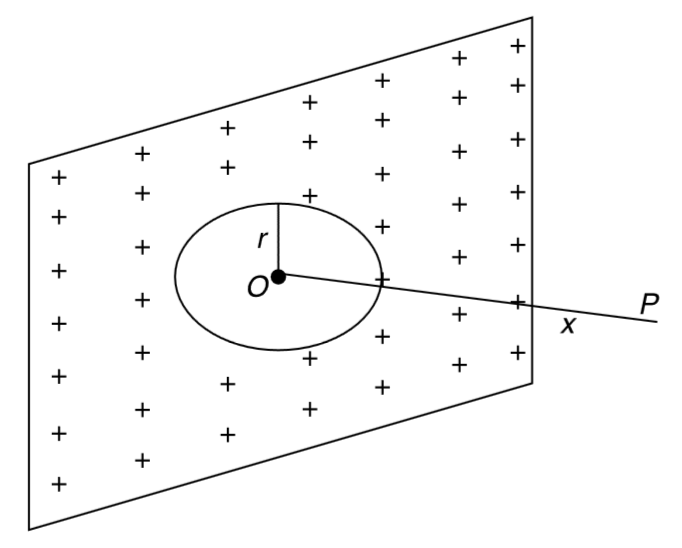 View Solution
View SolutionQuestion 18
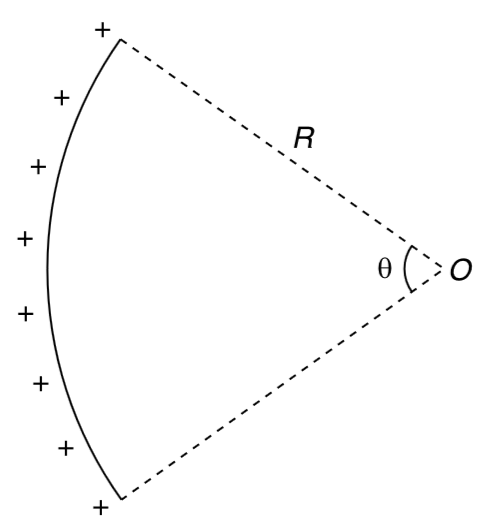
A thread having linear charge density λ is in the shape of a circular arc of radius R subtending an angle θ at the centre.
(a). Find the electric field at the centre.
(b). Using the epression obtained in part (a) find the field at the centre if the thread were emicircular
(c). Find the field at centre using the expression obtained in part (a) for the case θ→0. Is the result justified?
(d). A thread having total charge Q (uniformly distributed is in the shape of a circular arc of radius R subtending an angle θ at centre. write the expression for the field at the center. Obtain the field whenθ→0. Make sure you understand the difference in case. (c) and (d).
 View Solution
View SolutionQuestion 19
(a) There is an infinitely long thread uniformly charged with linear charge density λC/m. Using Gauss’ law, calculate the electric field (E0) at a distance x from the thread. (b) Now consider a semi-infinite uniformly charged thread (linear charge density =λ) as shown in figure. Find the y component of electric field at point P in terms of E0. Use simple qualitative argument. (c) For the situation described in (b) calculate the x component of electric field at point P using the method of integration. (d) Find the angle that the electric field at P makes with x direction.
 View Solution
View SolutionQuestion 22
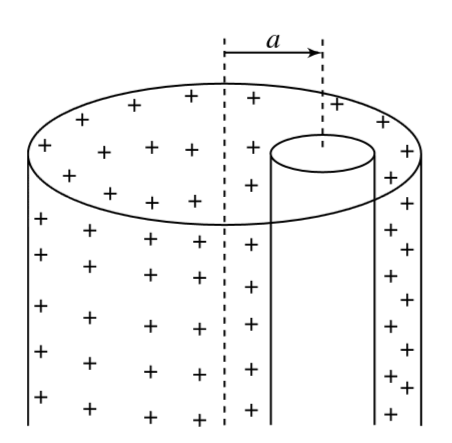
(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
 View Solution
View SolutionQuestion 23
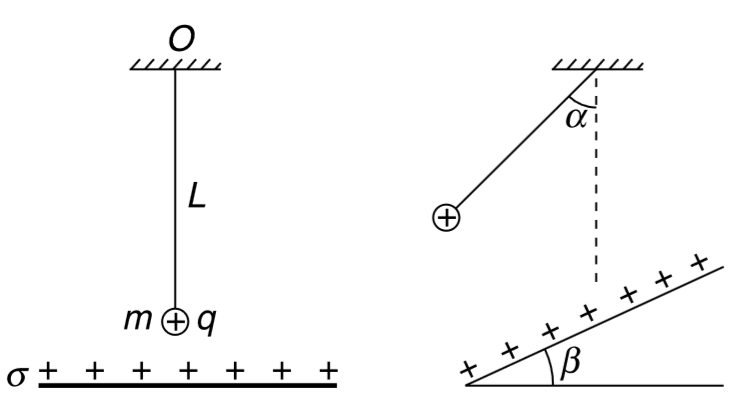
A pendulum has a bob of mass m carrying a positive charge q. Length of the pendulum string is L. Beneath the pendulum there is a large horizontal dielectric sheet of charge having uniform surface charge density of σC/m2. [figure (i)] (a) Find the time period of small oscillations for the pendulum (b) Now the dielectric sheet of charge is tilted so as to make an angle β with horizontal. Find the angle (a) that the thread makes with vertical in equilibrium position. Find time period of small oscillations in this case. [figure (ii)]
 View Solution
View SolutionQuestion 24
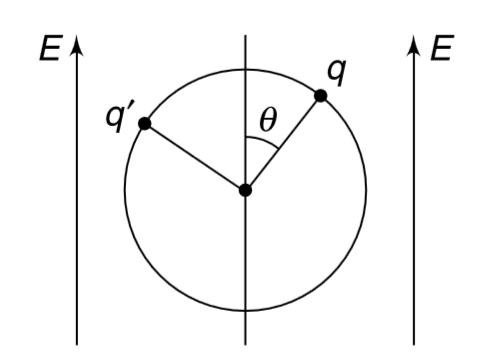
A uniform non conducting ring has mass m and radius R. tow point charges q and q' are fixed on its circumference at a separation of √2R the ring remains in equilibrium in air with its plane vertical in a region where exists a uniform vertically upward electric field E. Given E=4mg7q
(a) Find angle θ in equilibrium position (see figure). (b) The ring is given a small rotation in the plane of the figure and released. Will it perform oscillations? View SolutionQuestion 26
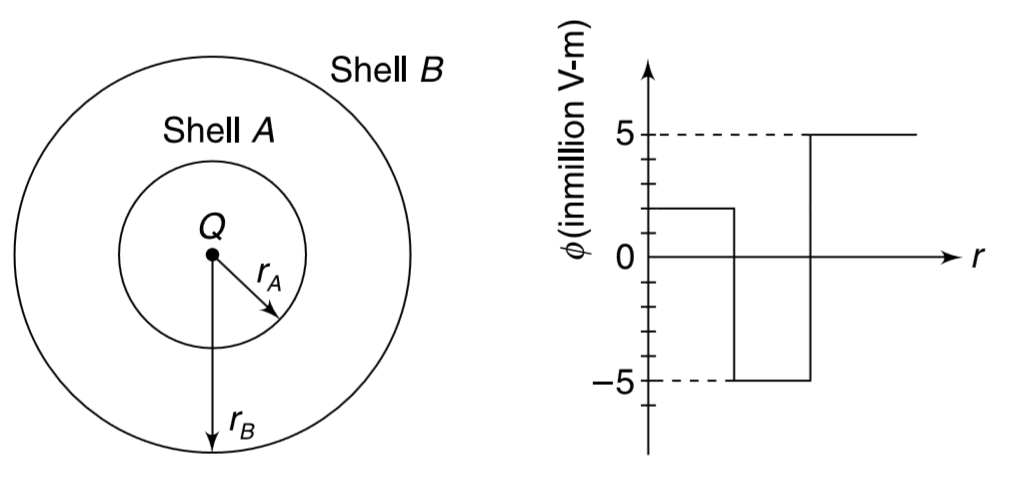
A charged particle is placed at the centre of two thin concentric spherical charged shells, made of non-conducting material. Figure A shows cross-section of the arrangement. Figure B gives the net flux ϕ through a Gaussian sphere centered on the particle, as a function of the radius r of the sphere. (a) Find charge on the central particle and shell A. (b) In which range of the finite values of r, is the electric field zero? View SolutionQuestion 27
There are two infinite slabs of charge, both of thickness d with the junction lying on the plane x = 0. The slab lying in the range 0 lt x lt d has a uniform charge density +ρ and the slab lying in the region – d lt x lt 0 has uniform charge density −ρ. Find the Electric field everywhere and plot its variation along the x axis. Note: This can be used to model the variation of electric field in the depletion layer of a p – n junction. View SolutionQuestion 30
A charge distribution generates a radial electrif field →E=ar2e−rkˆr, where r is distance from the origin ˆr is a unit vector in radial direction away from the origini and a and k are positive constants. The electric field extends around the origin up to a large distance.
(a). Find the charge (q0) that must be located at the origin to create such a field
(b). Find the quantity of charge (q) that must be spread around the charge q0 at origin to create such a field.View SolutionQuestion 33
Point charge q s placed at a point on the axis of a square non-conducting surface. The axis is perpendicular to the square surface and is passing through its centre. Flux of electric field throught he square caused due to charged q is ϕ. If the square is given a surface change of uniform density σ, find the force on the square surface due to point charge q.
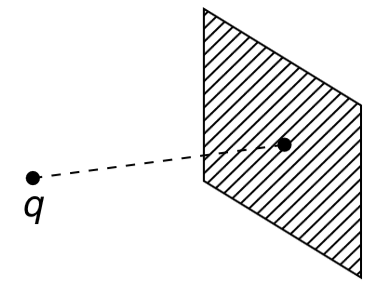 View Solution
View SolutionQuestion 34
In the figure shown sphere S1,S2 and S3 have radii R,R2andR4 respectively C1,C2 and C3 are centers of the three spheres lying in a plane Angle ∠C1C2C3 is right angle. Sphere S3 has a uniformly spread volume charge density 4ρ. the remaining pat of S2 has uniform charge density of 2ρ and the left over part of S1 has a uniform charge density of ρ.
(a) Find electric field at a point A at a distance R8 from C3 on the line, C2C3 (see figure)
(b). Find electric field at point B at a distance R4 from C2 on the line C3C2 (See figure)
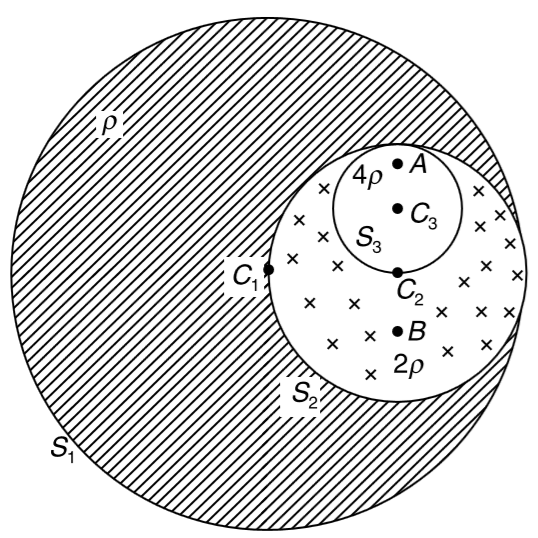 View Solution
View SolutionQuestion 35
An electron (charge = e, mass = m) is projected horizontally into a uniform electric field produced between two oppositely charged parallel plates, as shown in figure. The charge density on both plates is +- sigma C//m^2 and separation between them is d. You have to assume that only electric force acts on the electron and there is no field outside the plates. Initial velocity of the electron is u, parallel to the plates along the line bisecting the gap between the plates. Length of plates is 2L and there is a screen perpendicular to them at a distance L. (i) Find s if the electron hits the screen at a point that is at same height as the upper plate.
(ii) Final the angle q that the velocity of the electron makes with the screen while it strikes it.
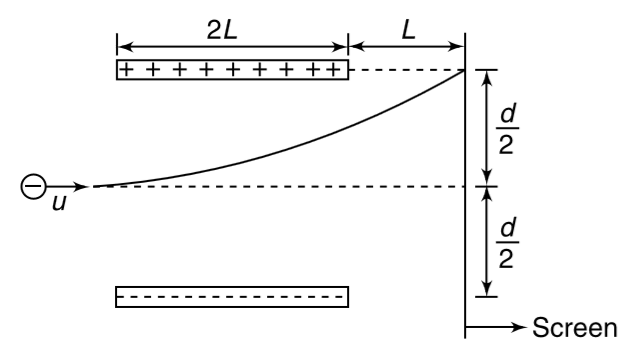 View Solution
View SolutionQuestion 36
A particle is projected at a speed of u = 40 m/s in vertically upward direction in a place where exists a horizontal uniform electric field E0. The specific charge of the particle is 4g3E0 . (a) Find the time after projection, when speed of the particle will be least. (b) Find the time (after projection) when displacement of the particle becomes perpendicular to its acceleration. (c) Assuming that the particle has been projected from a great height and the electric field is present in large region, what angle the velocity of the particle will make with horizontal after a long time? View SolutionQuestion 37
A charged particle having mass m I projected in a uniform electric field with a kinetic energy K0. After time t0 it was observed that the kinetic enrgy of the particle was K04 and its velocity was perpendicular to the field.
(a). (a) How much more time is required for the particle to regain its lost kinetic energy? (b) Write the impulse of the electric force acting on the particle between the two points where its kinetic energy is K0. Neglect all other forces on the particle apart from the electrostatic force.View SolutionQuestion 38
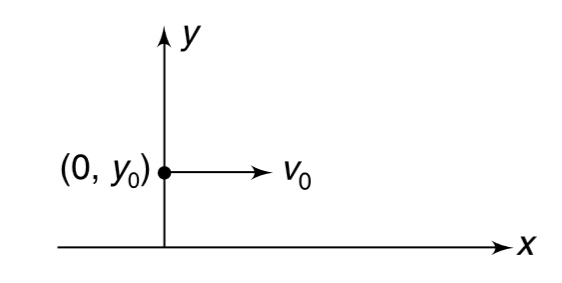
Electric field in xy plane is directed along positive y direction and its magnitude changes with y co-ordinate as E=ay2
A particle having charge q and mass m is projected at point (0,y0) with velocity
→v=v0ˆi
Neglect all other forces o the particle apart from the electric force. Calculate the slope of the trajectory of the particle as a function of y.View SolutionQuestion 41
Two point charges Q1 and Q2 lie along a line at a distance from each other. Figure 3.7 shows the potential variation along the line of charges. At which of the points 1, 2, and 3 is the electric field zero ? What are the singns of the charges Q1 and Q2 and which of the two charges is greater in magnitude ?
 .View Solution
.View SolutionQuestion 42
A uniform electric field exists in a region of space. Potential at potential O,A,B and C are V0=0 and VA=−1V,VB=−6V and VC=−3V respectively. Alll the cubes shown in fig have side length of 1m. ltbr> (a). Find VP−VQ
(b). Find the smallest distance of a point from O where the potential is −2V
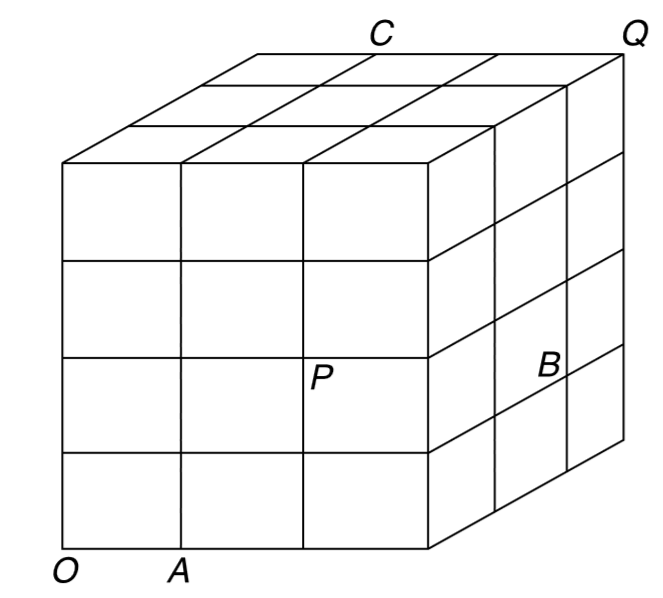 View Solution
View SolutionQuestion 43
It is known that there exists a uniform electric field in a certain region. Imagine an incline plane (figure) in the region which is inclined at θ=37∘ to the horizontal when one moves horizontally along the incline from A to B (AB=1cm), the electric potential decreases by 10V. Similarly, potential at C(AC=1cm) is less than potential at A by 10 V where line AC lies on the incline and is perpendicualr to AB. When one moves vertically up from point A to a point D(AD=1cm), the potential drop by 10 V again. Find the magnitude of the electric field in the region and the angle that it makes with vertical [given sin37∘=35]
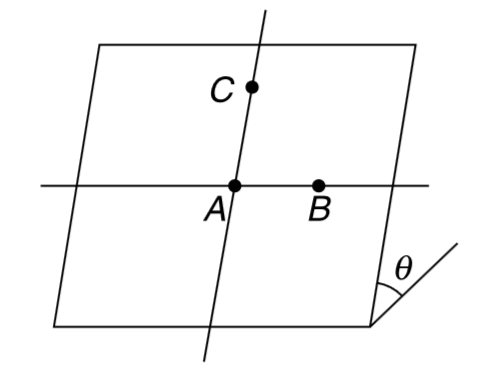 View Solution
View SolutionQuestion 45
Electric field in a three dimensional space is directed radially towards a fixed point and its magnitude varies with distance (r) from the fixed point as E = 4r V/m (a) Draw electric field lines to approximately represent such a field.
(b) Calculate the quantity of charge present inside a spherical volume of radius a centered at the fixed point.
(c). Find potentail difference (VA−VB) between two points A(1,1,√2) m and B(0,3,4)m take the fixed point to be the origin.View SolutionQuestion 46
When a conducting disc is made to rotate about its axis, the centrifugal force causes the free electrons to be pushed toward the edge. This causes a sort of polarization and an electric field is induced. The radial movement of free electrons stops when electric force on an electron balance the centrifugal force. Calculate the potential difference developed across the centre and the edge of a disc of radius R rotating with angular speed ω. [This potential difference is sometimes called as sedimentation potential]. Take mass and charge of an electron to be m and e respectivelyView SolutionQuestion 48
A metallic sphere of radius R has been charged to a potential of V = 100 volt. A thin hemispherical conducting shell has dimensions so that it can just fit on the half of the metallic sphere. The shell is originally grounded. Now, using an insulating handle, it is placed on top of the charged sphere so as to perfectly cover its top half. The shell is removed from the sphere and again grounded. After this the shell is again placed on the sphere, removed and then grounded. The process is continued till the potential of the sphere becomes V' = 6.25 volt. How many times the shell was placed on the sphere? View SolutionQuestion 50
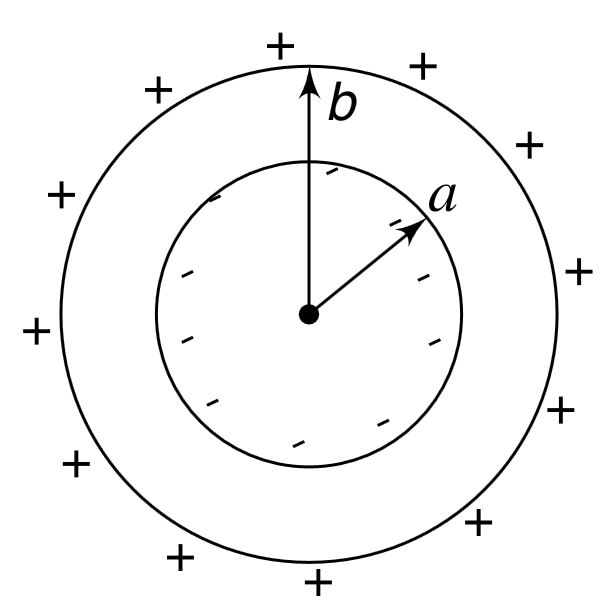
A thick conducting spherical shell of inner radius a and outer radius b is shown in figure. It is observed that the inner face of the shell carries a uniform charge density −σ. The outer surface also carries a uniform surface charge density +σ.
(a) Can you confidently say that there must be a charge inside the shell? Find the net charge present on the shell. (b) Find the potential of the shell. View SolutionQuestion 56
A solid spherical conductor of radius R has a spherical cavity inside it (see figure). A point charge q is placed at the centre of the cavity. (a) What is the potential of the conductor? (b) If the charge q is shifted inside the cavity by a distance Δx, how does the potential of the conductor change? (c) How does your answer to the question (a) and (b) change if the cavity is not spherical and the charge q is placed at any point inside it (see figure) (d) Draw electric field lines in entire space in each case. In which case all field lines are straight lines
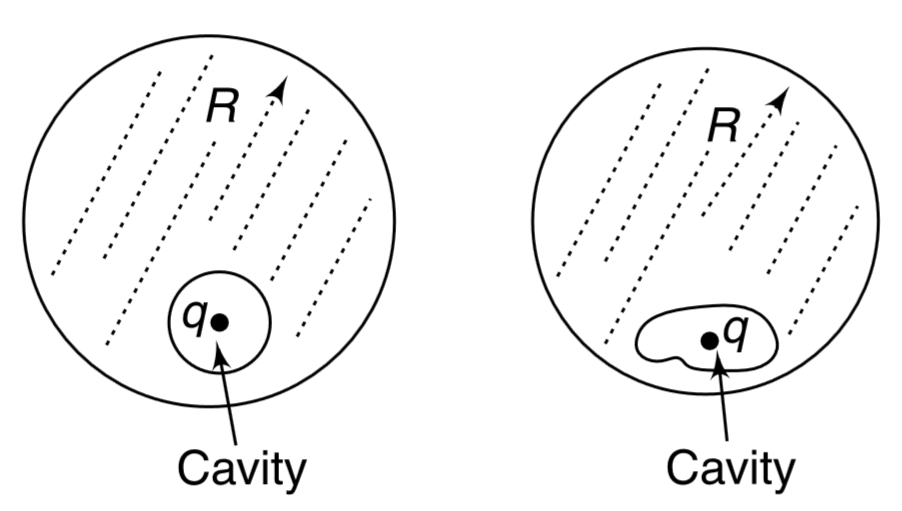 View Solution
View SolutionQuestion 57
Conducting ball of radius a is surrounded by a layer of dielectric having inner radius a and outer radius b. The dielectric constant is K. The conducting ball is given a charge Q. Write the magnitude of electric field and electric potential at the outer surface of the dielectric.
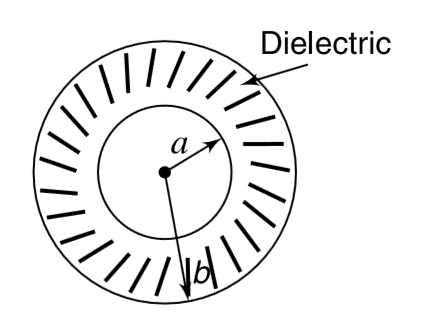 View Solution
View SolutionQuestion 58
A point charge q is placed at a distance x from the centre of a conducting sphere of radius R(lt x). (a) How much charge will flow through the switch S when it is closed to ground the sphere? (b) Find the current through the switch S when charge ‘q’ is moved towards the sphere with velocity V.
 View Solution
View SolutionQuestion 60
Two concentric spherical shells have radii R and 2R. The outer shell is grounded and the inner one is given a charge +Q. A small particle having mass m and charge – q enters the outer shell through a small hole in it. The speed of the charge entering the shell was u and its initial line of motion was at a distance a=√2R from the centre. (a) Find the radius of curvature of the path of the particle immediately after it enters the shell. (b) Find the speed with which the particle will hit the inner sphere. Assume that distribution of charge on the spheres do not change due to presence of the charge particle
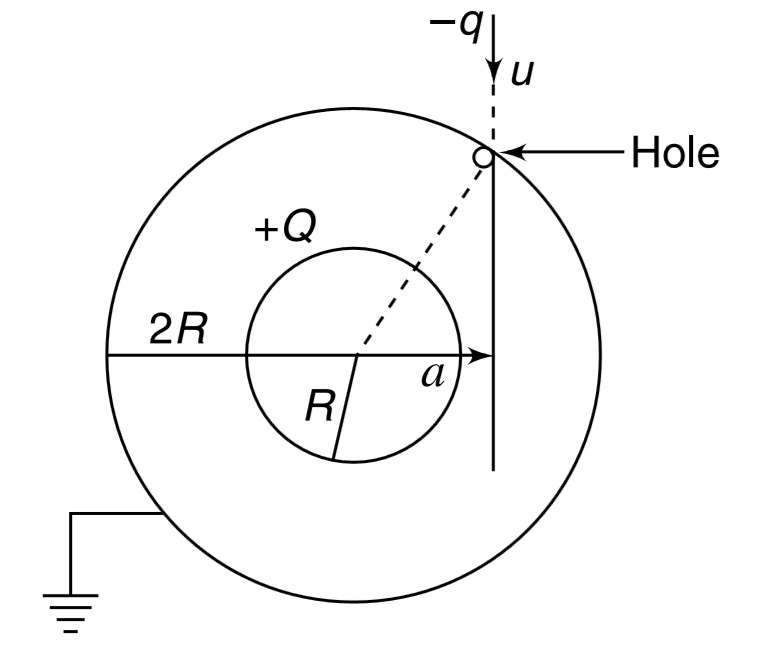 View Solution
View SolutionQuestion 61
There charges q, 3q and 12q are to be placed on a straight line AB having 12 cm length. Two of the charges must be placed at end points A and B and the third charge can be placed anywhere between A and B. Find the position of each charge if the potential energy of the system is to be minimum. In the position of minimum potential energy what is the force on the smallest charge?View SolutionQuestion 62
Two square of sides a and 2a are placed in xy plane with their centers at the origin. Two charges, – q each, are fixed at the vertices of smaller square (lying on X axis). Two charges, Q each, are fixed at the vertices of bigger square on the X axis (see figure). (a) Find work required to slowly move the larger square to infinity from the position shown. (b) Find work done by the external agent in slowly rotating the inner square by 90∘ about the Y axis followed by a rotation of 90∘ about the Z axis.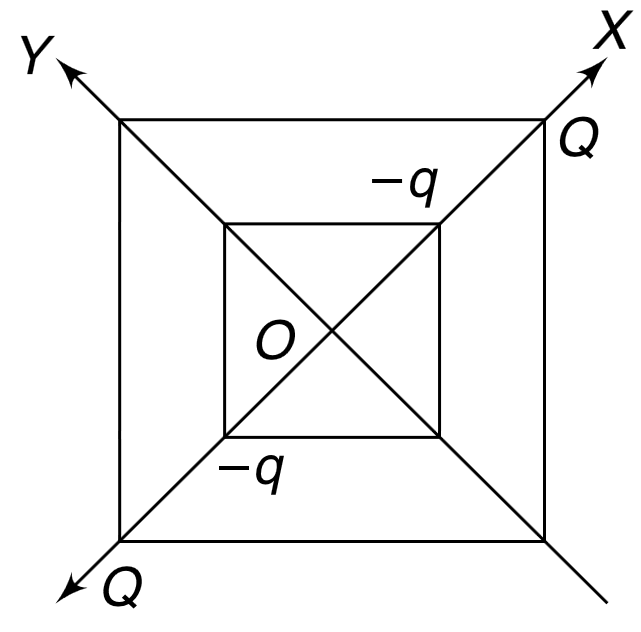 View Solution
View SolutionQuestion 63
A certain charge distribution produces electric potential that varies along the X axis as shown in figure. [There is no field in y or z direction] (a) At which point (amongst A, B, C, D and E) does a negative charge feel the greatest force in positive X direction? (b) Find the upper limit of the speed that a proton can have, as it passes through the origin, and still remain bound near the origin. Mass and charge of a proton are m and e. How will your answer change for an electron?
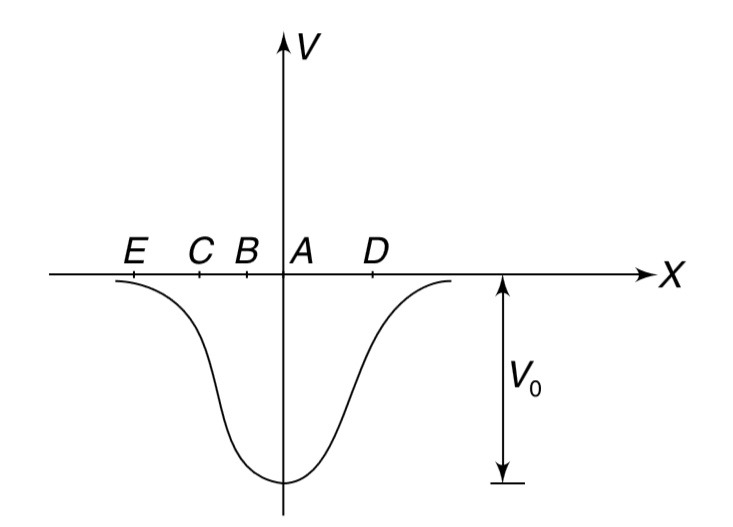 View Solution
View SolutionQuestion 65
Below the fixed end O of the insulating horizontal thread OB, there is a fixed charge A of Q=20μc. At the end B of the thread there is a small mass m carrying charge Q=20moc. The mass is released from the position shown and it is found to come to rest when the thread becomes vertical. Assume that the thread does not hit the fixed charge at A. [g=10m/s2] (a) Find mass m. (b) Find tension in the thread in the equilibrium position when the thread is vertical. (c) Is the equilibrium mentioned in (b) stable or unstable?
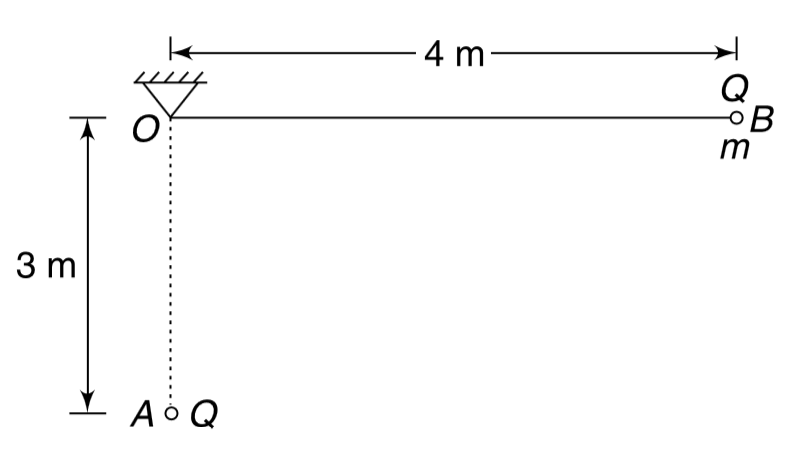 View Solution
View SolutionQuestion 66
A small positively charged ball of mass m is suspended by an insulating thread of length L. This ball remains in equilibrium with string horizontal when another small charged ball is placed exactly at a distance L below the point of suspension of the first ball. The second ball is slowly moved away from the first ball to a far away point. (The second ball is moved horizontally so that the first ball does not accelerate). As a result the first ball lowers down to the original position of the second ball and the string become vertical. Find the work done by the external agent in removing the second ball.
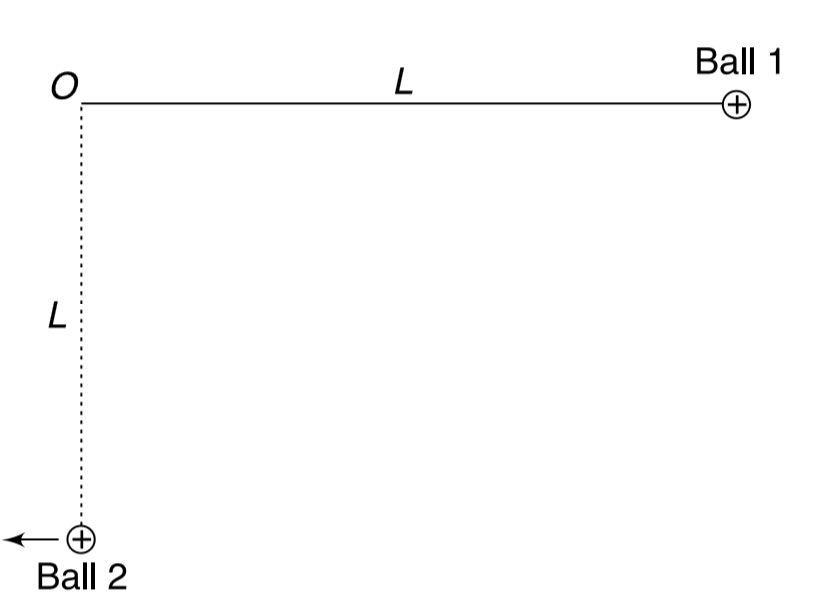 View Solution
View SolutionQuestion 67
A particle (A) having charge Q and mass m is at rest and is free to move. Another particle (B) having charge q and mass m is projected from a large distance towards the first particle with speed u. (a) Calculate the least kinetic energy of the system during the subsequent motion. (b) Find the final velocity of both the particles. Consider coulomb force only. View SolutionQuestion 68
In the last question, the two particles A and B are initially held at a distance r=qQ2π∈0mu2 apart. Particle B is projected directly towards A with velocity u and particle A is released simultaneously. Find the velocity of particle A after a long time. Consider coulomb force only. View SolutionQuestion 69
Two positively charged balls having mass m and 2 m are released simultaneously from a height h with horizontal separation between them equal to x0. The ball with mass 2 m strikes the ground making an angle of 45∘ with the horizontal. (a) At what angle, with horizontal, the other ball hits the ground? (b) Find the work done by the electrostatic force during the course of fall of the two balls. View SolutionQuestion 70
A and B are two concentric spherical shells made of conductor. Their radii are R and 2R respectively. The two shells have charge Q and – 2Q on them. An electron escapes from the surface of the inner shell A and moves towards a small hole in the outer shell B. (a) What shall be the minimum kinetic energy of the emitted electron so that it can escape to infinity through the small hole in outer shell? (b) What will be your answer if charge on both the shells were +Q? Charge on electron = e.
 View Solution
View SolutionQuestion 71
A thin uniform rod of mass M and length 2L is hinged at its centre O so that it can rotate freely in horizontal plane about the vertical axis through O. at its ends the insulating rod has two point charges 2q and q (see figure). An electrif field E is switched on making and angle θ0=60∘
with the initial position of the rod. The field is uniform and horizontal. (a) Calculate the maximum angular velocity of the rod during subsequent motion. (b) Find the maximum angular acceleration of the rod.
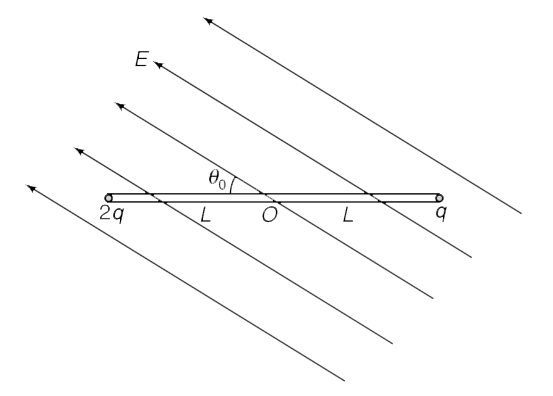 View Solution
View SolutionQuestion 72
Two charge particles are moving such the distance between them remains constant. The ratio of their masses is 1 : 2 and they always have equal and opposite momentum. The particles interact only though electrostatic force and no other external force is acting on them. The electrostatic interaction energy for the pair of the particles is –U0. Find the kinetic energy of the lighter particle. How does the kinetic energy change with time? View SolutionQuestion 73
Two blocks A and B are connected by a spring made of a non conducting material. The blocks are placed on a non conducting smooth horizontal surface (see figure). The wall touching A is also non conducting. Block A carries a charge – q. There exists a uniform electric field of intensity E0 in horizontal direction, in the entire region. Find the value of minimum positive charge Q that we must place on block B and release the system so that block A subsequently leaves contact with the wall. Force constant of the spring is k. Neglect interaction between charges on the blocks.
 View Solution
View SolutionQuestion 74
Large number of identical conducting spheres have been laid as shown in figure. Radius of each sphere is R and all of them are uncharged. Switch S1 is closed to connect sphere 1 to the positive terminal of a V volt cell whose other terminal is grounded. After some time switch S1 is opened and S2 is closed. Thereafter, S2 is opened and S3 is closed, next S3 is opened and S4 is closed. The process is continued till the last switch is closed. Consider the cell and spheres to be your system and calculate the loss in energy of the system in the entire process.
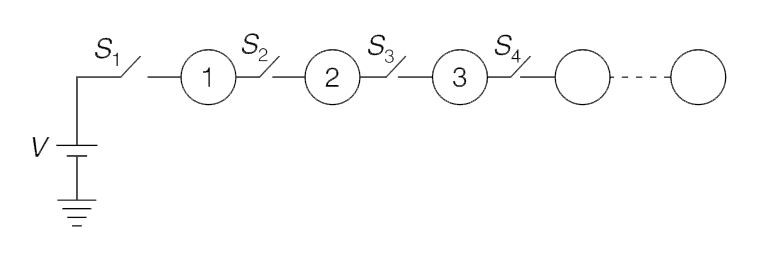 View Solution
View SolutionQuestion 76
Two identical electric dipoles are arranged parallel to each other with separation between them large compared to the length of individual dipole. The electrostatic energy of interaction of the two dipoles in this position is U. (a) Find work done in slowly rotating one of the dipoles by 90∘ so as to bring it to position shown in Fig. (b). (b) Find work done in rotating one of the dipoles by 180∘ so as to bring it to the position shown in Fig. (c). O1 and O2 are centers of the dipoles.
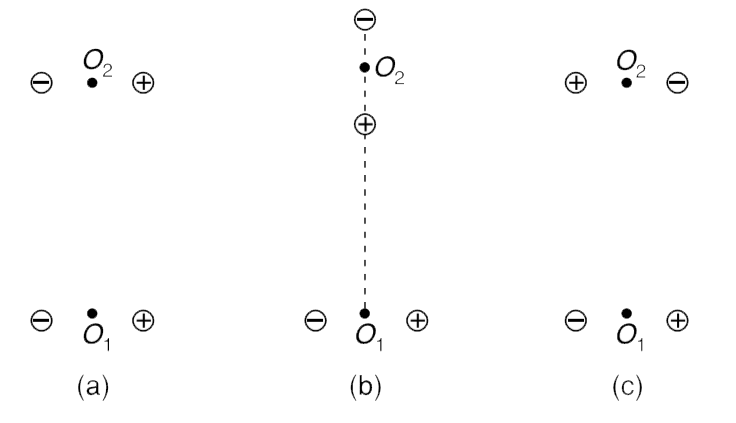 View Solution
View SolutionQuestion 77
A ring of radius r has a uniformly spread charge + q on quarter of its circumference. The opposite quarter of the ring carries a charge – q uniformly spread over it. Find the electric potential at a point A shown in the figure. Point A is at a distance R(gtgt r) from the centre of the ring.
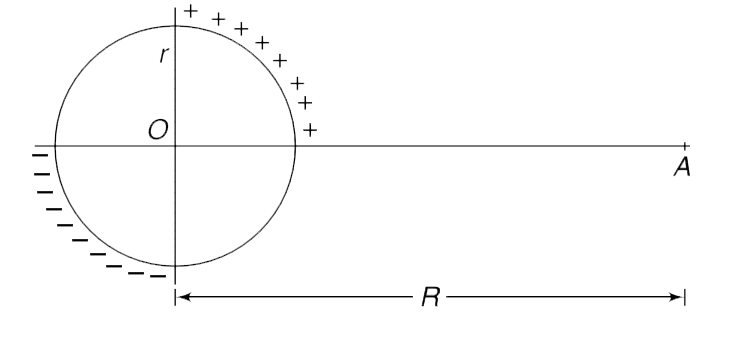 View Solution
View Solution