Level 1 from ARIHANT PHYSICS Chapter 5 ELECTROSTATICS for Class 12

Class 12	PHYSICS
Chapter	ELECTROSTATICS
ARIHANT PHYSICS	Level 1
Medium	English
Academic Year	2023-2024

Question 1
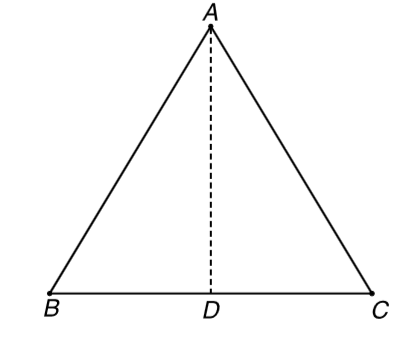
(a) Six equal charges have been placed at the vertices of a regular hexagon. Charge at vertex A is moved to the centre of the hexagon and there it experiences a net electrostatic force of magnitude F. Charge at E is also moved to the centre so as to double the magnitude of the charge at the centre. Calculate the magnitude of the electrostatic force that this central charge experiences now. (b) Three charges of equal magnitude lie on the vertices of an equilateral triangle ABC. All of them are released simultaneously. The charge at A experiences initial acceleration along AD where D is the midpoint of the side BC. Find the direction of initial acceleration of the charge at B.

View Solution
Question 2
Two identical small conducting balls have positive charges $q_{1}$ and $q_{2}$ respectively. The force between the balls when they are placed at a separation is F. The balls are brought together so that they touch and then put back in their original positions. Prove that the force between the balls now, cannot be less than F. View Solution
Question 3
Point charges $- q, 2 q, - 3 q, q, - q, 2 q, - 3 q, q, - q, 2 q, - 3 q$ , and q have been placed at marks $1, 2, 3, 4, 5 ... . .12$ respectively on the circular dial of a clock. Find the electric field intensity at the centre of the dial if distance of each charge from the centre is r.View Solution
Question 4
Let $q_{1}$ be a positive charge equal to the magnitude of the total charge on all electrons present in 0.9 mg of pure water and $q_{2}$ be the charge on a 6.35 mg copper sphere from which 0.1% of its total electrons have been removed. Avogadro’s number, $N_{A} = 6 \times 10^{23}$
Molar mass of $H_{2} O = 18 g$
Molar mass of $C u = 63.5 g$
(a) Find force between $q_{1}$ and $q_{2}$ if they are placed at a separation of 1 km. (b) How does this force compare with the weight of a car having mass of 1200 kg? What conclusion can you draw from the result? View Solution
Question 5
Three point charges $q_{1} = q, q_{2} = q and q_{3} = Q$ are placed at points having poisition vetors $\to r_{1}, \to r_{2}$ and $({\to r}_{1} + {\to r}_{2})$ respectively. It is known that $| {\to r}_{1} | = | {\to r}_{2} | = \to r$ . The net electrostatic force on $q_{3}$ is $\sqrt{3}$ times the force applied by either of $q_{1}$ or $q_{2}$ on $q_{3}$ . find ${\to r}_{1} \cdot {\to r}_{2}$ .View Solution
Question 6
Two stiff non conducting rods have length L each and have small balls connected to their ends. The rods are placed parallel to each other and the balls are connected by two identical springs as shown. When each ball is given a charge q, the system stays in equilibrium when it is in the shape of a square. If natural relaxed length of each spring is L/2 find the force constant (k) for them.
View Solution
Question 7
Five identical charges, $q_{1}$ each, are placed at the vertices of a regular pentagon having side length $l_{1}$ . The net electrostatic force on any of the charges due to other four is $F_{1}$ . Find the electrostatic force $F_{2}$ on any one of the five identical charges, $q_{2}$ each, placed at the vertices of a regular pentagon having side length $l_{2}$ . View Solution
Question 8
A simple pendulum has a bob of mass m which carries a charge q on it. Length of the pendulum is L. There is a uniform electric field E in the region. Calculate the time period of small oscillations for the pendulum about its equilibrium position in following cases:
(i). E is vertically down having magnitude $E = \frac{m g}{q}$
(ii). E is vertically up having magnitude $E = \frac{2 m g}{q}$
(iii). E is horizontal having magnitude $E = \frac{m g}{q}$
(iv). E has magnitude of E=q and is directed upward making an angle $45^{\circ}$ with the horizontal View Solution
Question 9
Two identical negative charges are fixed on X axis at equal distances from the origin (O). A particle having positive charge starts at a large distance from O, moves along the Y axis, passes through the origin and moves far away from O in the positive Y direction. Describe qualitatively how its acceleration charges as it moves. Draw a rough graph showing the variation of acceleration (a) vs position of the particle (y). Take the acceleration of the particle to be positive in + Y direction. View Solution
Question 10
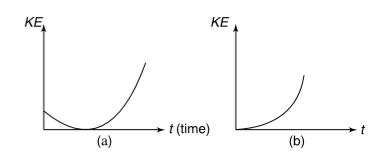
An electron is either released from rest or projected with some initial velocity in a uniform electric field. Neglect any other force on the electron apart from electrostatic force. Which of the graphs shown in fig could possibly represent the change in kinetic energy of the electron during its course of motion? Explain the situation in each case.

View Solution
Question 11
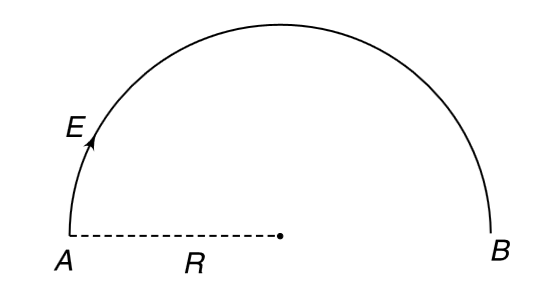
In a region of space an electric field line is in the shape of a semicircle of radius R. Magnitude of the field at all point is E. A particle of mass m having charge q is constrained to move along this field line. The particle is released from rest at A. (a) Find its kinetic energy when it reaches point B. (b) Find the acceleration of the particle when it is at midpoint of the path from A to B.
View Solution
Question 12
Electric field E = – bx + a exists in a region parallel to the X direction (a and b are positive constants). A charge particle having charge q and mass m is released from the origin X = 0. Find the acceleration of the particle at the instant its speed becomes zero for the first time after release. View Solution
Question 13
A Sphere of radius $R_{0}$ carries a volume charge density proportional to the distance (x) from the origin, $ρ = α x$ where $α$ is a positive constant. (a) Calculate the total charge in the sphere of radius $R_{0}$ . (b) The sphere is shaved off so as to reduce its radius. What should be the radius (R) of the remaining sphere so that it contains half the charge of the original sphere? (c) Find the electric field at a point inside the sphere at a distance r lt R. Give your answer for original sphere of radius $R_{0}$ as well as for the smaller sphere of radius R that was left after shaving off the original sphere. View Solution
Question 14
Draw electric field lines for charge distributions given below– (a) Two equal point charges placed at a separation. (b) Two point charges 2q and – q placed at a separation. Describe qualitatively how the lines will appear at a very large distance from the two charges? (c) Three point charges, each equal to + q placed at the vertices of an equilateral triangle.View Solution
Question 15
Three conducting concentric spherical shells of radii R, 2R and 3R carry some charge on them. The potential at the centre is 50 V and that of middle and outer shell is 20 V and 10 V respectively. Find the potential of the inner Shell.View Solution
Question 16
The potential at a point in an electric field is give by $V = R r$ volt where r is distance of the point from the origin of the co-ordinate system. Find the electric field at a point $r = (ˆ i + 2 ˆ j + 2 \sqrt{5} ˆ k) m$ View Solution
Question 17
Electric potential in a 3 dimensional space is given by $V = (\frac{1}{x} + \frac{1}{y} + \frac{2}{z})$ volt where x,y and z are in meter. A particle has charge $q = 10^{12} C$ and mass $m = 10^{- 9} g$ and is constrained to move in xy plane. Find the initial acceleraton of the particle if it is released at (1,1,1)m.View Solution
Question 18
A metal plate M is grounded. A point charge + Q is placed in front of it. Consider two points A and B as shown in fig. At which point (A or B) is the electric field stronger? At which point is the potential higher?
View Solution
Question 19
Equipotential lines arising from a static charge distribution has been shown in a certain region of space. (a) Draw the electric field lines starting from point A (b) If a charge is released at A, will it move along the field line passing through A? (c) How much work is done by the electric force if a charge moves from B to C? Is the knowledge of path important in this calculation?
View Solution
Question 20
(a). The equipotential curves in x,y plane are given by $x^{2} + y^{2} = V$ when V si potential Draw the rough sketch of electric field lines in x-y plane.
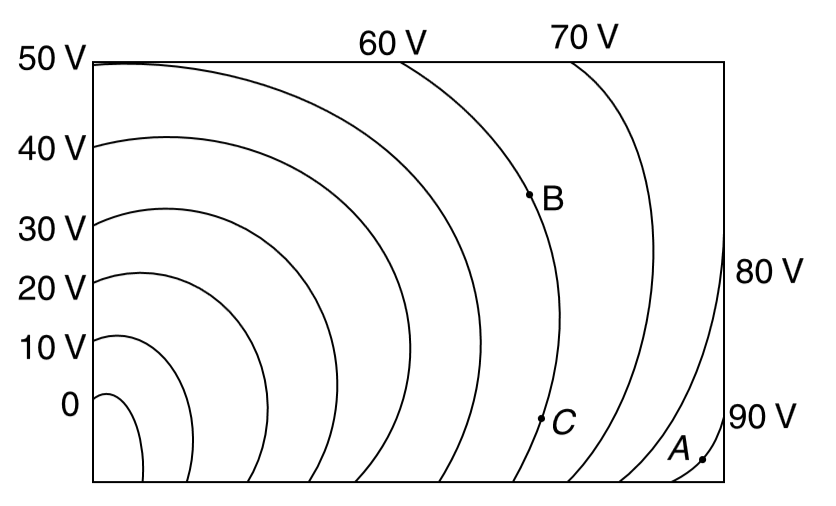(b). Repeat the above question if the potential field is given by $V = x^{2} + y^{2} - 4 x + 4$ View Solution
Question 21
Four point charges q, q, q and – q are placed at the vertices of a square of side length a. The configuration is changed and the charge are positioned at the vertices of a rhombus of side length a with – q charge at the vertex where angle is $120^{\circ}$ . Find the work done by the external agent in changing the configuration.
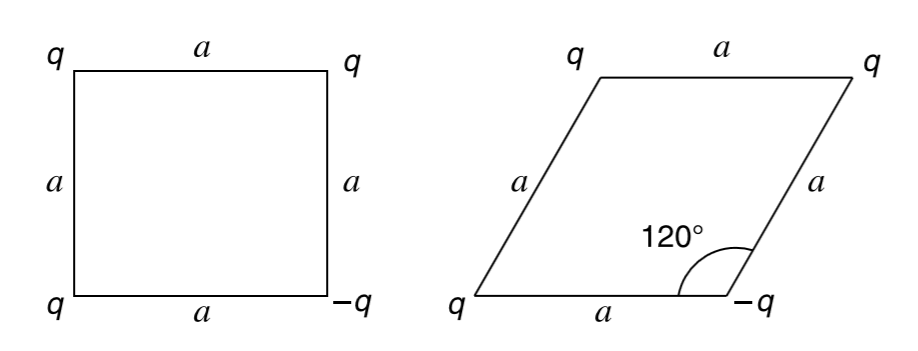View Solution
Question 22
There is a ball of radius r having uniformly distributed volume charge Q on it and there is a spherical shell of radius r having uniformly distributed surface charge Q on it. The two spheres are far apart. (a) A point charge q is moved slowly from the centre of the shell (through a small hole in it.) to the centre of the ball. Find work done by the external agent in the process. (b) The two spheres are brought closer so that their centers are separated by 4r. Now calculate the amount of work needed in slowly moving a point charge q from the centre of the shell to the centre of the ball. Assume that charge on one ball does not alter the charge distribution of the other. Does your answers in (a) and (b) differ? Why?
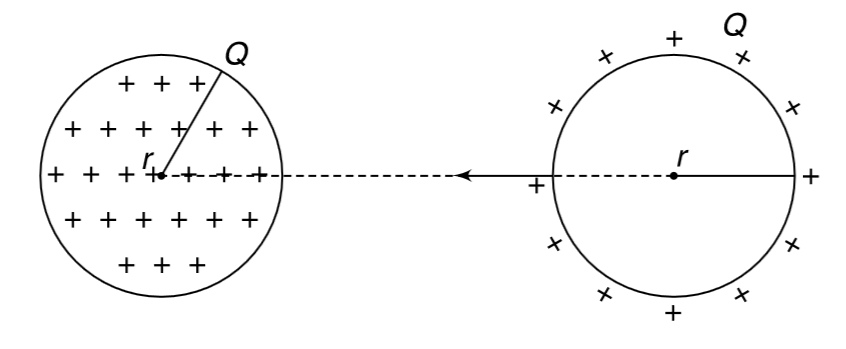View Solution
Question 23
A uniformly charged sphere has charge Q. An electron (charge – e, mass m) revolves around it in a circular orbit of radius r. (a) Write the total energy (i.e., sum of its kinetic energy and electrostatic potential energy in the field of the sphere) of the electron. (b) If the time period of revolution of the electron in circular orbit of radius r is T, then find the time period if the orbital radius is made 4r.View Solution
Question 24
A uniformly charged sphere has radius R and charge Q on it. A negatively charged particle having mass m and charge – q shoots out of the surface of the sphere with speed V. The minimum speed $(V_{0})$ for which the particle escapes the attraction of the sphere may be called as escape speed. Will the value of $V_{0}$ depend on magnitude of q? [Recall that escape speed of a body from the surface of the earth does not depend on its mass]. View Solution
Question 25
There is a uniform horizontal electric field of strength E in a region. A pendulum bob is pulled to make the string horizontal and released. The bob has mass m and charge q. (a) Find the maximum angle $(θ_{0})$ that the bob swings before coming to rest momentarily. (b) Find E if the bob comes to rest when the string is vertical.
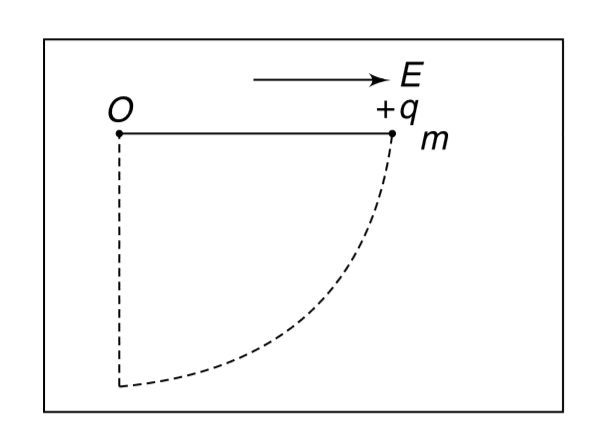View Solution
Question 26
A conducting sphere of radius R carries a charge Q. It is enclosed by another concentric spherical shell of radius 2R. Charge from the inner sphere is transferred in infinitesimally small installments to the outer sphere. Calculate the work done in transferring the entire charge from the inner sphere to the outer one. View Solution
Question 27
The ratio of energy density in electrif field $(u_{E})$ to square of potential $(V^{2})$ at a point A at a distnance x from a static point charge Q is $η$
(a). Write the value of the ratio at a distance 2x from the point charge Q.
(b). Write the dimensional formula for the ratio $η$ View Solution
Question 28
(a). Calculation the largest possible electrostatic energy in $1 c m^{3}$ volume of air.t he dielectric breakdown of air happens when field exceeds $3 \times 10^{6} V / m$
(b). A conducting ball of radius 10 cm is placed in distilled water $(\in_{r} = 80)$ and charged with a charge $Q = 2 \times 10^{- 9} C$ . Calculated the energy used up in charging the ball.View Solution
Question 29
Three short electric dipoles, each of dipole moment P, are placed at the vertices of an equilateral triangle of side length L. Each dipole has its moment oriented parallel to the opposite side of the triangle as shown in the fig. Find the electric field and potential at the centroid of the triangle
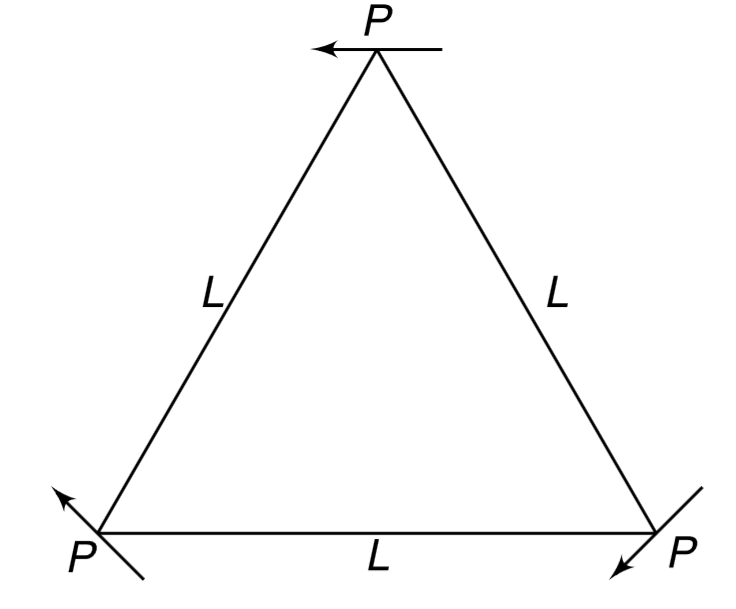View Solution
Question 30
Short electric dipole of dipole moment P is placed at the centre of a ring of radius R having charge Q uniformly distributed on its circumference. The dipole moment vector is along the axis of the ring. Find force on the dipole due to the ring. View Solution
Question 31
Calculate the electric dipole moment of a system comprising of a charge + q distributed uniformly on a semicircular arc or radius R and a point charge – q kept at its centre.View Solution

All Exercises from ARIHANT PHYSICS Class 12 PHYSICS ELECTROSTATICS

Home
Ask Doubt
Profile