Exercise 2.2 from CENGAGE PHYSICS Chapter 47 WAVE OPTICS for Class 12

Question 1

Question 2

Question 3

Question 4

Question 5

Question 6

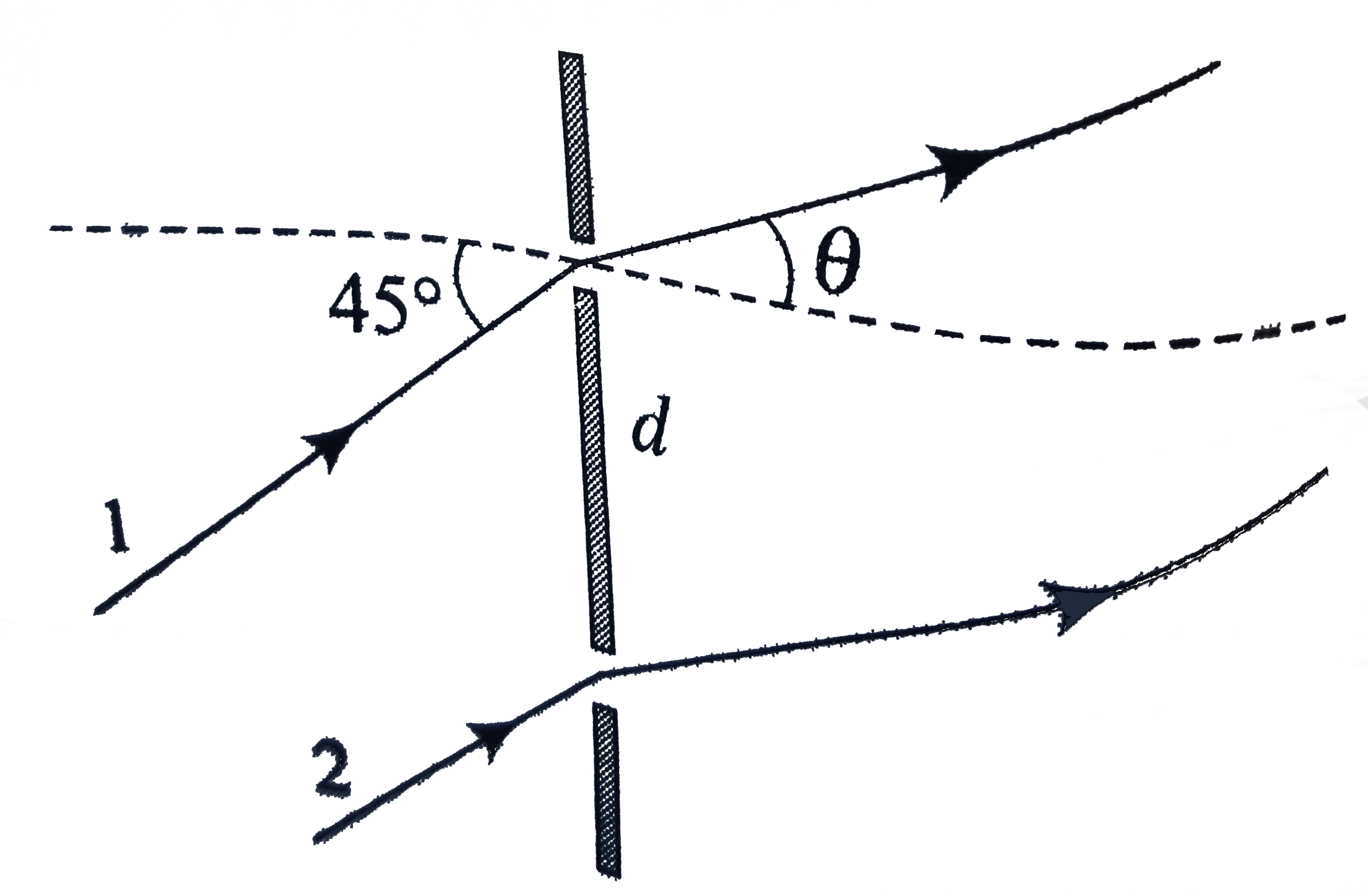
Question 7

Question 8

Question 9

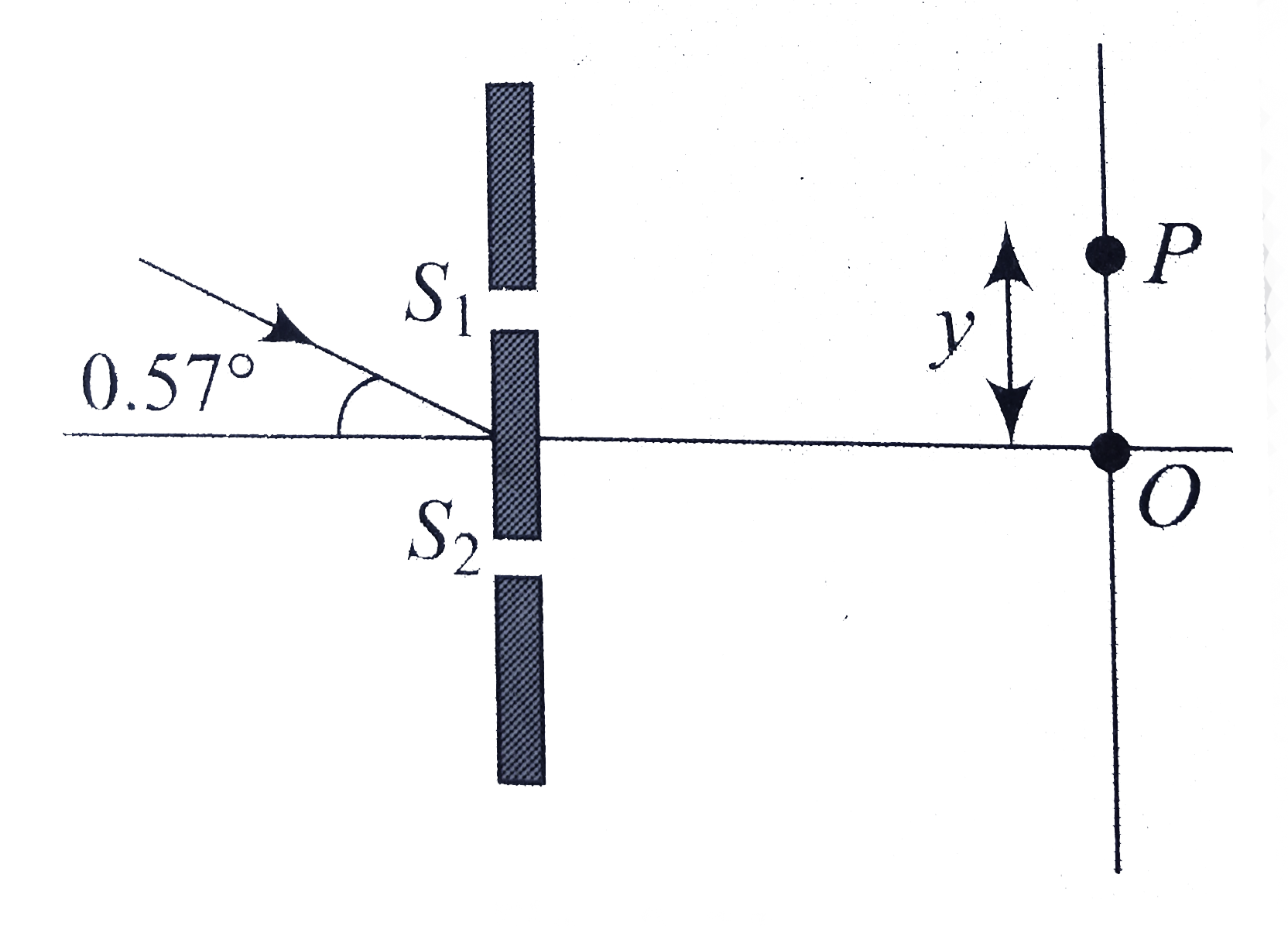
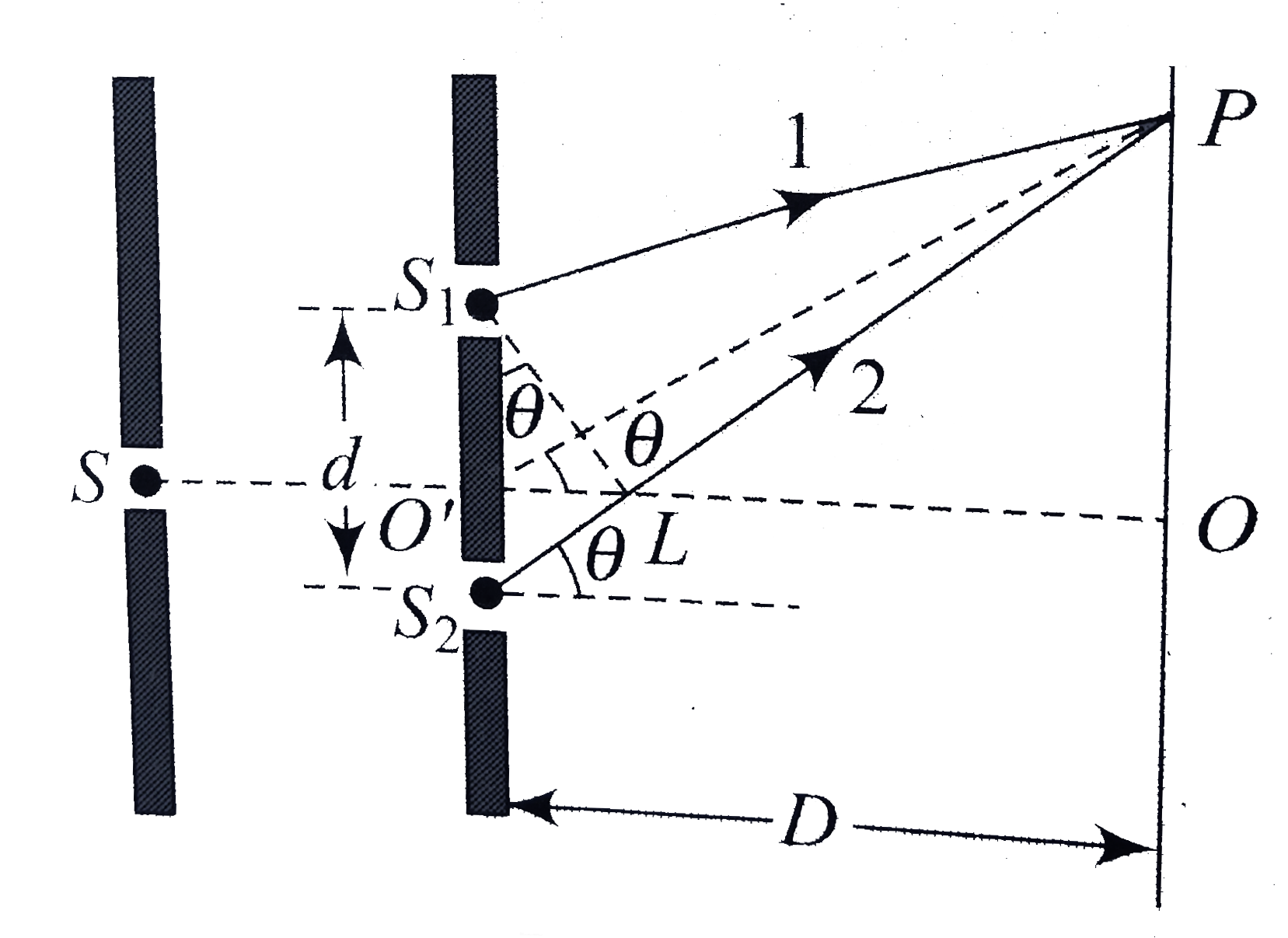
In YDSE with $D=1m,d=1mm$, light of wavelength $500nm$ is incident at an angle of ${0.57}^{\circ }$ w.r.t. the axis of symmetry of the experimental set-up. If center of symmetry of screen is O as shown figure.
a. find the position of centrla maxima,
b. find intensity at point O in terms of intensity of central maxima $I_0$, and
c. find number of maixma lying central maxima.
.

Question 10

In Young's experiment, find the distance between two slits that results in the third minimum for $420nm$ violet light at an angle ${30}^{\circ }$
.

Question 11

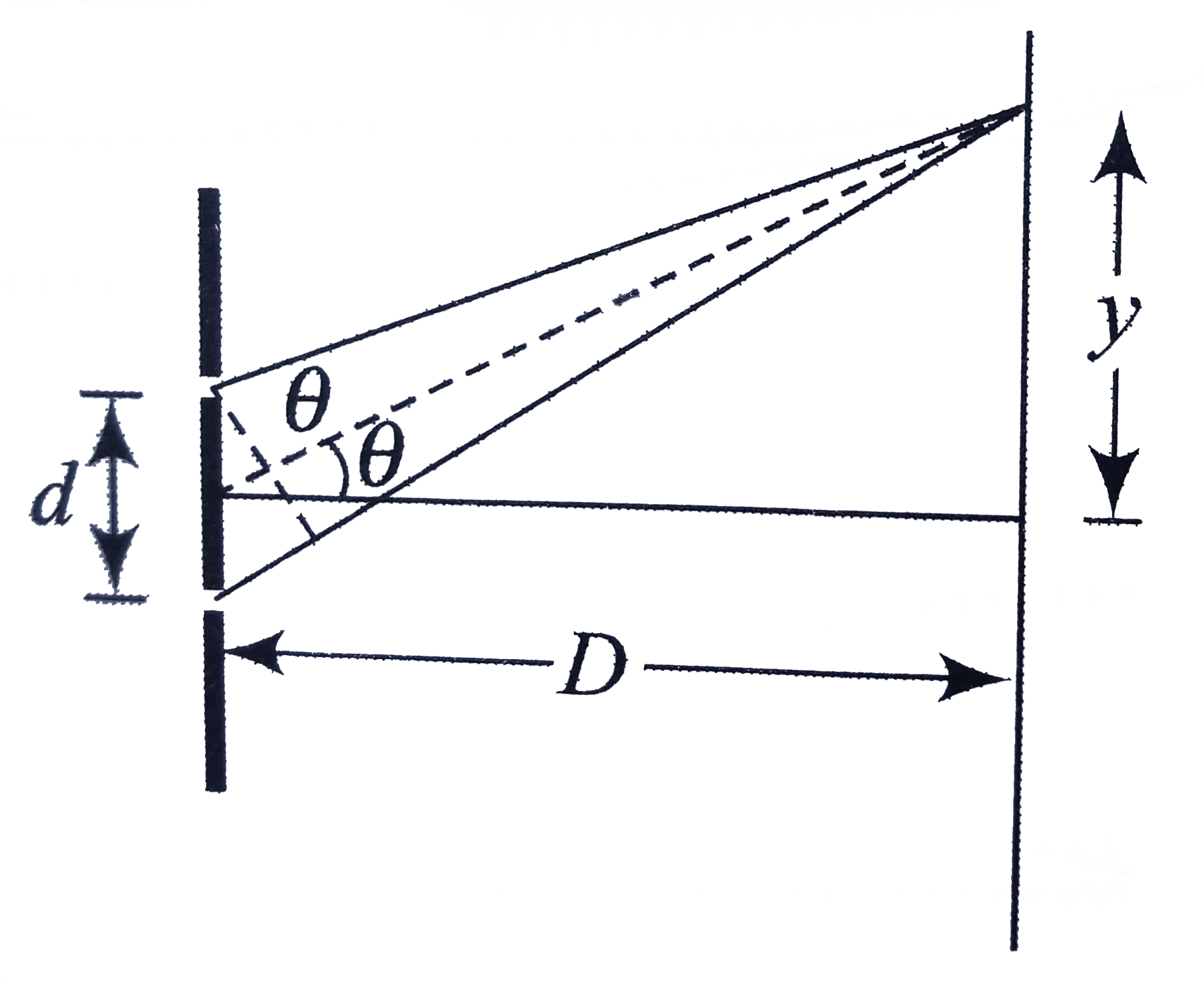
In an interference arrangement similar to double-slit experiment, $S_1$ and $S_2$ are illuminated with coherent source microwave source each of frequency 1 MHz. the sources are synchronized to have zero phase difference . This slits are separated by distance $d=150.0m$ The intensity $I\left(\theta \right)$ is measured as a funciton of $\theta$, where $\theta$ is defined as shown in figure. If $I_0$ is maximum intensity, calculate $I\left(\theta \right)$
For :
a. $\theta =0$ b. $\theta ={30}^{\circ }$
c. $\theta ={90}^{\circ }$

Question 12

Question 13

Question 14

Question 15

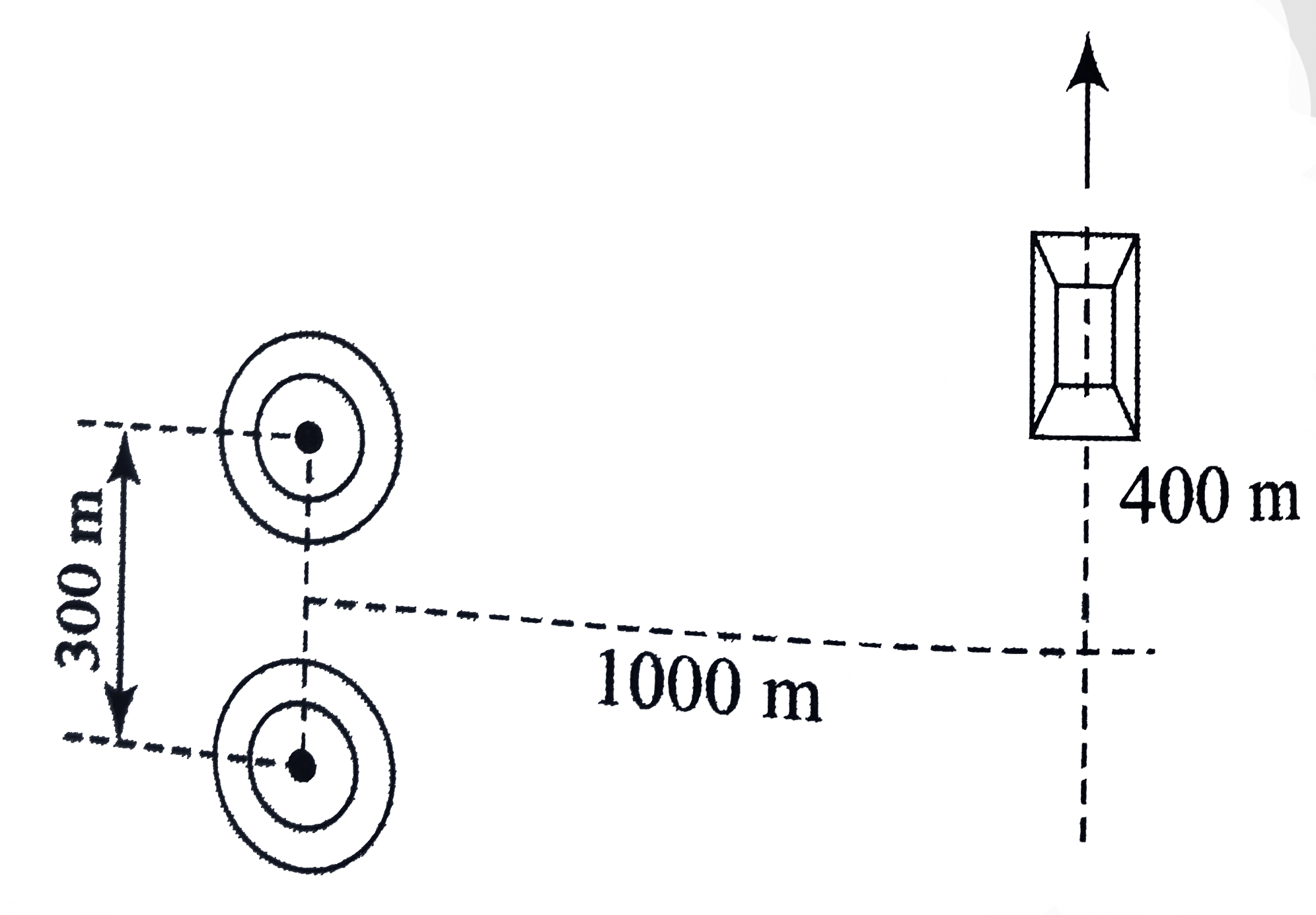
Two radio antennas separated by 300 m as shown in figure simultaneously broadcast indentical singals at the same wavelength. A radio in a car traveling due north receives the signals. (a) If the car is at the position of the second maximum, what is the wavelength of the signals? (b) How much farther must the car travel to encounter the next mininum in reception? (Note: Do not use the small- angle approximation in this problem.)

Question 16

Question 17

Question 18

Question 19

Distance between the slit shown in figure is $d=20\lambda$, where $\lambda$ is the wavelength of light used. Find the angle $\theta$ where
a. central maxima (where path difference is zero) is obtained, and
b. third-order maxima is obtained.

Question 20

Question 21

Question 22