Illustrative Example from GK PUBLICATIONS PHYSICS (HINGLISH) Kinetic Theory of Gases and Gas Laws for Class 12
| Class 12 | PHYSICS |
| Chapter | Kinetic Theory of Gases and Gas Laws |
| GK PUBLICATIONS PHYSICS (HINGLISH) | Illustrative Example |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
A cylindrical container is shown in figure-2.7 in which a gas is enclosed. Its initial volume is Vand temperature is T. As no external pressure is applied on the light piston shown, gas pressure must be equal to the atmospheric pressure. If gas temperature is doubled, find its final volume. In its final state if piston is clamped and temperature is again doubled, find the final pressure of the gas.
 View Solution
View SolutionQuestion 2
Two glass bulbs of equal volume are connected by a narrow tube and are filled with a gas at 0∘C and a pressure of 76cm of mercury. One of the bulbs is then placed in melting ice and the other is placed in a water bath maintained at 62∘C. What is the new value of the pressure inside the bulbs? The volume of the connecting tube is negligible.View SolutionQuestion 7
A smooth vertical tube having two different cross sections is open from both the ends but closed by two sliding pistions as shown in Fig. and tied with an inextensible string. One mole of an ideal gas is enclosed between the piston The difference in cross-sectional areas of the two pistons is given ΔS. The masses of piston are m1 and m2 for larger and smaller one, respectively. Find the temperature by which tube is raised so that the pistons will be displaced by a distance l. Take atmospheric pressure equal to P0
 View Solution
View SolutionQuestion 8
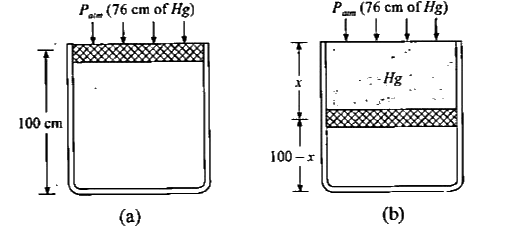
A vertical cylinder of height 100 cm contains air at a constant temperature and its top is closed by a frictionless piston at atmospheric pressure (76 cm of Hg) asshown in figure-2.12. If mercury is slowly poured on the piston, due to its weight airis compressed. Find the maximum height of the mercury column which can be put on the piston.
 View Solution
View SolutionQuestion 9
A vertical hollow cylinder of height 1.52m is fitted with a movable piston of negligible mass and thickness. The lower half portion of the cylinder contains an ideal gas and the upper half is filled with mercury. The cylinder is initially at 300K. When the temperature is raised half of the mercury comes out of the cylinder. Find this temperature assuming the thermal expansion of the mercury to be negligible.
 View Solution
View SolutionQuestion 10
A tall cylindrical vessel with gaseous nitrogen is located in a uniform gravitational field in which the free-fall acceleration is equal to g. The temperature of the nitrogen varies along the height h so that its density is the same throught the volume. find the temperature gradient dT/dh.View SolutionQuestion 11
An open glass tube is immersed in mercury in such a way that a lenth of 8cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46cm. What will be length of the air column above mercury in the tube now?
(Atmosphere pressure =76cm of Hg)View SolutionQuestion 12
A uniform tube closed at one end, contains a pellet of mercury 10cm long. When the tube is kept vertically with the closed-end upward, the length of the air column trapped is 20cm. Find the length of the air column trapped when the tube is inverted so that the closed-end goes down. Atmospheric pressure=75cm of mercury.View SolutionQuestion 13
Fig. shows a horzontal cylindrical container of length 30cm, which is partitioned by a tight-fiting separator. The separator is diathermic but conductws heat very slowly. Initially the separator is the state shown in the figure. The temperature of left part of cylinder is 100K and that on right part is 400K. Initially the separator is in equilibrium. As heat is conducted from right to left part, of separator after a long when gases on the two displacement of separator after a long when gases on the two parts of cylinder are in thermal equilibrium.
 View Solution
View SolutionQuestion 18
A parallel beam of nitrogen molecules moving with velocity v=400ms−1 imprings on a wall at an angle θ=30∘ to its normal. The concentration of molecules in the beam is n=9×1018cm−3. Find the pressure exerted by the beam on the wall, assuming that collisions are perfectly elastic.View SolutionQuestion 20
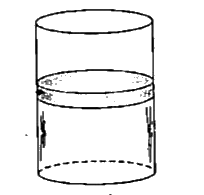
Figure-2.28 shows a cylindrical container which is divided in two equal parts by a clamped diathermic piston. Different ideal gases are filled in the two parts. It is found that the rms speed of molecules in the lower part is equal to the mean speed of molecules in the upper part. Find the ratio ofmass of molecule of gas in lower part to that of the gas in upper part.
 View Solution
View SolutionQuestion 21
In a closed container of volume 10−3m3,O2 gas is filled at temperature 400 K and pressure 1.5 atm. A small hole is made in the container from which gas leaks out to pen atmosphere. After some time the temperature and pressure of container become equals to that of surrounding. Find the mass of gas that leaks out from the container. (Atmospheric temperature = 300 K) View SolutionQuestion 24
Calculate (a) the average kinetic energy of translation of an oxygen molecule at 27∘C (b) the total kinetic energy of an oxygen molecule at 27∘C (c ) the total kinetic energy in joule of one mole of oxygen at 27∘. Given Avogadro's number =6.02×1023 and Boltzmann's constant =1.38×10−23J/(mol−K).View SolutionQuestion 25
Calculate (a) the average kinetic energy of translation of an oxygen molecule at 27∘C (b) the total kinetic energy of an oxygen molecule at 27∘C (c ) the total kinetic energy in joule of one mole of oxygen at 27∘. Given Avogadro's number =6.02×1023 and Boltzmann's constant =1.38×10−23J/(mol−K).View SolutionQuestion 26
Calculate (a) the average kinetic energy of translation of an oxygen molecule at 27∘C (b) the total kinetic energy of an oxygen molecule at 27∘C (c ) the total kinetic energy in joule of one mole of oxygen at 27∘. Given Avogadro's number =6.02×1023 and Boltzmann's constant =1.38×10−23J/(mol−K).View SolutionQuestion 30
A cubical vessel of side 1 m contains one mole of nitrogen at a temperature of 300 K. If the molecuels are assuming to move with the rms velocity
further if the vessel now thermally insulated moved with a constant speed v and then suddenly stopped and this results in rise of temperature by 2∘C, find v. View SolutionQuestion 31
As adiabatic vessel contains n1=3 mole of diatomic gas. Moment of inertia of each molecule is I=2.76×10−46kgm2 and root-mean-square angular velocity is ω0=5×1012rad/s. Another adiabatic vessel contains n2=5 mole of a monatomic gas at a temperature 470K. Assume gases to be ideal, calculate root-mean-square angular velocity of diatomic molecules when the two vessels are connected by a thin tube of negligible volume. Boltzmann constant k=1.38×10−23J/:molecule.View Solution