Diffraction Of Light from IE IRODOV PHYSICS Chapter 9 OPTICS for Class 12
| Class 12 | PHYSICS |
| Chapter | OPTICS |
| IE IRODOV PHYSICS | Diffraction Of Light |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
A plane light wave falls normally on a diaphragm with round aperature opening the first N Fresnel zones for a point P on a screen located at a distance b form the diaphragm. The wavelength of light is equal to λ. Find the intensity of light I0 in front of the diaphragm if the distribution of intensity of light I(r) on the screen is knows. Here r is the distance from the point P.View SolutionQuestion 2
A point source of light with wavelength λ=0.50μm is located at a disatnce a=100cm in front of a diaphragm with round aperture of radius r=1.0mm. Find the distance b between the diaphragm and the observation point for which the number of Fresnel zones in the aperture equals k=3.View SolutionQuestion 3
A diaphram with round aperture, whose radius r can be varited during the experiment, is placed between a point source of light and a screen. The distance from the diaphram to the source and the screen are equal to a=100cm and b=125cm. determie the wavelength of light if the intensity maximum at the centre of the differaction pattern of the screen is observed at r1=1.00mm and the next maximum at r2=1.29mm.View SolutionQuestion 4
A plane monochromatic light wave with intensity I0 falls normally on an opaque screen with a round aperture. What is the intensity of light I behind the screen at the point for which the aperture
(a) is equal to the first Fresnel zone, to the internal half of the first zone,
(b) was made equal to the first Fresnel zone and then half of it was closed (along the diameter) ?View SolutionQuestion 5
A plane monochromatic light wave with intensity I0 falls normally on an opaque disc closing the first Fresnel zone for the observation point P. What did the intensity of light I at the point P become equal to after
(a) half of the disc (along the diameter) was removed,
(b) half of the external half of the first Fresnal zone removed (along the diameter)?View SolutionQuestion 6
A plane monochromatic light wave with intensity I0 falls normally on the surfaces of the opaque screens shown in Fig. Find the intensity of light I at a point P

(a) located behind the corner ponts of screens 1−3 and behind the edge of half-plane 4,
(b) for which the rounded-off edge of screens 5−8 coincides with the boundary of the first formula describing the result obtained for screens 1−4, the same, for screens 5−8.View SolutionQuestion 7
A plane light wave with wavelength λ=0.60μm falls normally on a sufficiently large glass plate having a round recess on the oppiste side (Fig.) For the observation point P that recess correcponds to the first one and and a half Fresnel zones. Find the depth h of the recess at which the intensity of light at the point P is
(a) maximum,
(b) minimum,
(c ) equal to the intensity of incident light.
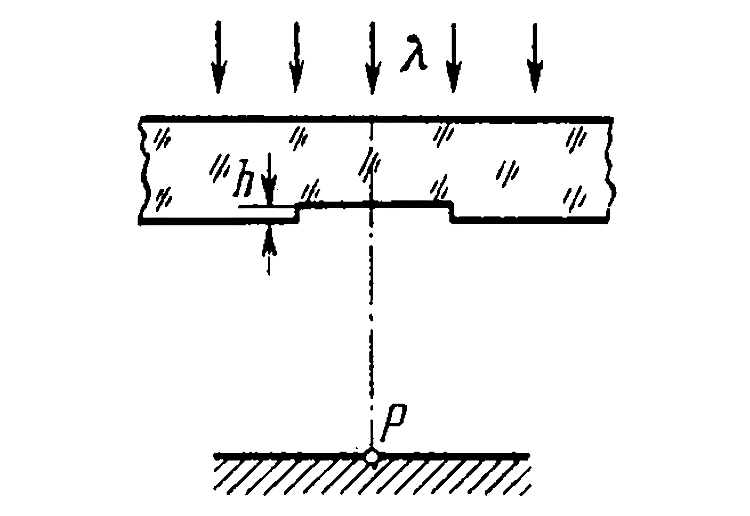 View Solution
View SolutionQuestion 8
A plane light wave with wavelength λ and intensity I0 falls normally on a large glass plate whose opposite side serves as an opaque screen with a round aperture equal to the first Fresnel zone for the observation point P. In the middle of the aperture there is a round recess equal to half the Fresnel zone. What must the depth h of that recess be for the intensity of light at the point P to be the highest? What is this intensity equal to?View SolutionQuestion 9
A plane light wave with wavelength λ=0.57μm falls normally on a suface on a surface of a glass (n=1.60) disc which shuts one and a half Fresnel zones for the observation point P. What must the minimum thickness of that disc be for the intensity of light at the point P to be the highest ? Take into account the interference of light on its passing through the disc.View SolutionQuestion 10
A plane light wave with wavelength λ=0.54μm goes through a thin converging lens with focal length f=50cm and an aperture stop fixed immediately after lens, and reaches a screen placed at a distance b=75cm from the aperture stop. At what aperture radii has the centre of the differaction pattern on the screen the maximum illuminance ?View SolutionQuestion 11
A plane monochromatic light wave falls normally on a round aperture. At a distance b=9.0m from it there is a screen showing a certain diffraction pattern. The aperture diameter was decreased η=3.0 times. Find the new distance b' at which the screen should be positioned to obtain the diffraction pattern simialer to the previous one but diminished η times.View SolutionQuestion 12
An opaque ball of diameter D=40mm is placed between a source of light with wavelength λ=0.55μm and a photographic plate. The distance between the source and the ball is equal to a=12m and that between the ball and the photographic plate is equal to b=18m. find:
(a) the image dimension y' on the plate if the transverse dimension of the source is y=6.0mm,
(b) the minimum height of irregularities, covering the surface of the ball at random, at which the ball obstructs light.
Note: As calculations and experience shown, that happens when the height of irregularities is comparable with the width of the Fresnel zone along which the edge of an opaque screen passes.View SolutionQuestion 14
A plane light wave with wavelength λ=0.60μm and intensity I0 falls normally on a large glass plate whose side view is shown in Fig. At what height h of the ledge will be intensity of light at points located directly below be
(a) minimum,
(b) twice as low as I0 (the losses due to reflection are to be neglected).
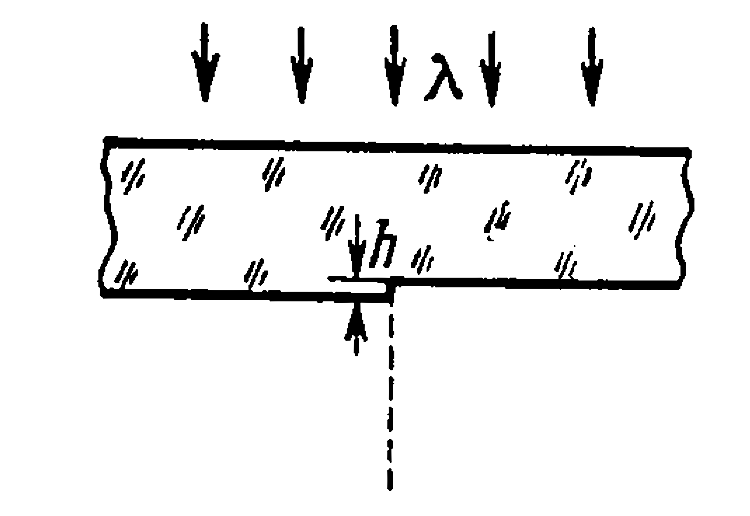 View Solution
View SolutionQuestion 15
A plane monochromatic light wave falls normally on an opaque half-plane. A screen is located at a distance b=100cm behind the half-plane. Making use of the cornu spiral (Fig.) find :
(a) the ratio of intensities of the first maximum and the neighbouring minimum,
(b) the wavelength of light if the first two maxima are separated by a distance Δx=0.63mm.
 View Solution
View SolutionQuestion 16
A plane light wave wityh wavelength 0.60μm falls normally on a long opaque strip 0.70mm wide. Behind it a screen is placed at a distance 100cm. Using Fig. find the ratio of intensities of light in the middle of the diffraction pattern and at the edge of the geometrical shadow.
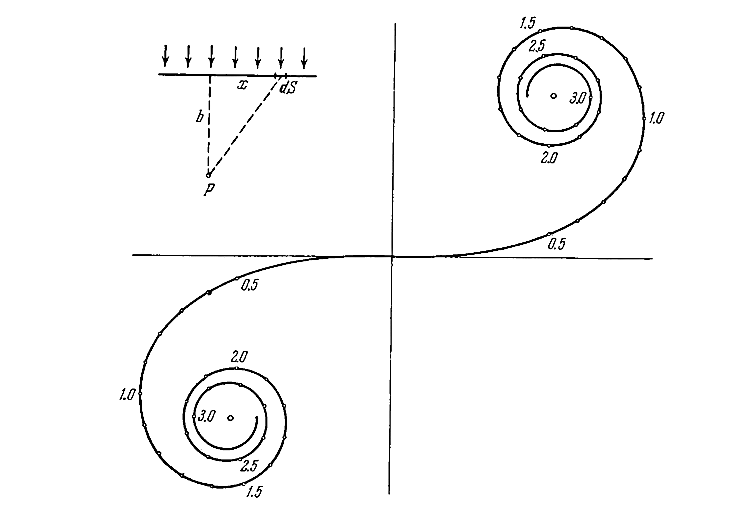 View Solution
View SolutionQuestion 17
A palne monochromatic ligth wave falls normally on a long rectangular slit behind which a screen is positioned at a distance b=60cm. First the width of the slit has adjucted so that in the middle of the diffraction pattern the lowest minimum was observed. After widening the slit by Δh0.70mm, the next minimum was obtained in the centre of the pattern. Find the wavelength of light.View SolutionQuestion 18
A plane light wave with wavelength λ=0.65μm falls normally on a large glass plate whose opposite side has a longrectangular recess 0.60mm wide. Using Fig. find the depth H of the recess at which the diffraction pattern on the screen 77cm away from the plate has the maximum illuminance at its centre.
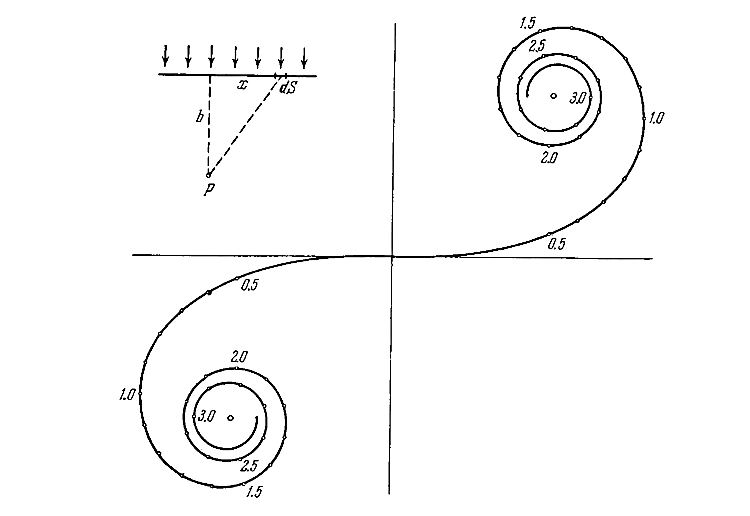 View Solution
View SolutionQuestion 19
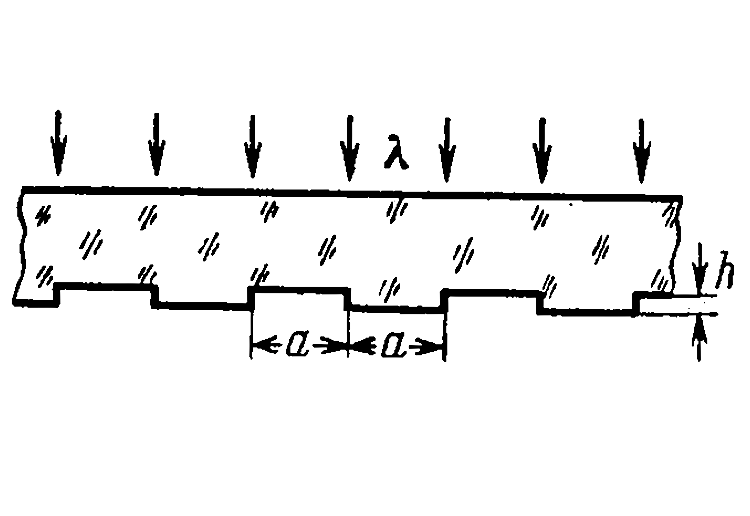
A plane light wave with wavelength λ=0.65μm falls normally on a large glass plate whose opposite side has a large and an opaque strip of width a=0.30mm (Fig.) A screen is placed at a distance b=110cm from the plate. The height h of the ledge is such that the intensity of light at point 2 of the screen is the heighest possible. making use of Fig. find the ratio of intensities at point 1 and 2.
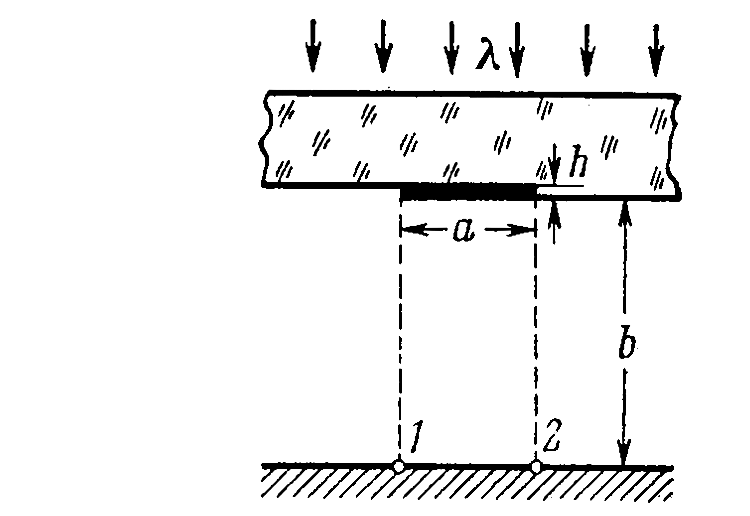
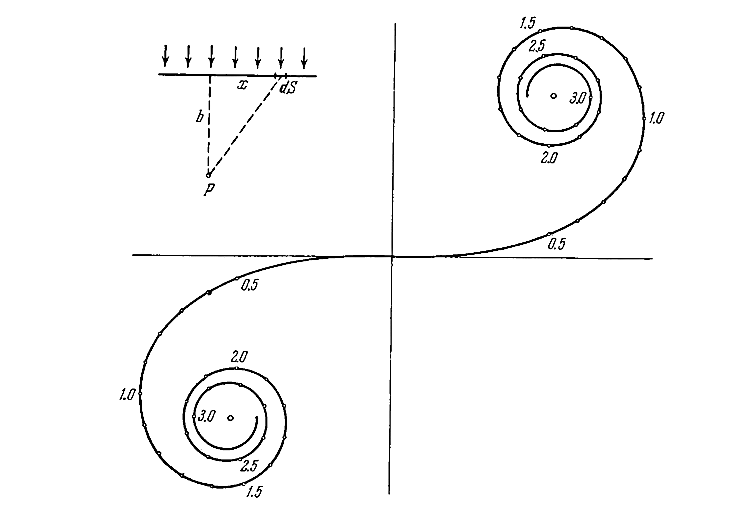 View Solution
View SolutionQuestion 20
A plane monochromatic light wave of intensity I0 falls normally on an opaque screen with a long slit having a semicircular cut on one side (Fig.) The edge of the cut coincides with the boundary line of the first Fresnel zone for the observation point P. Thw width of the slit measure 0.90 of the radius of the cut. using Fig. find the intensity of light at the point P.
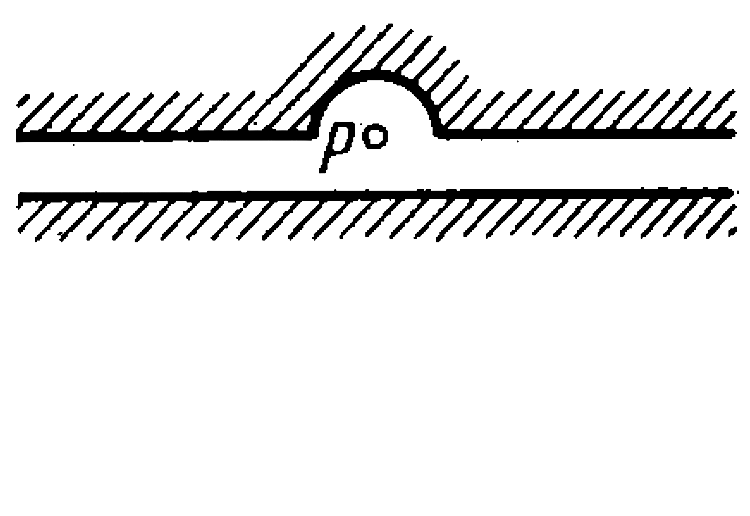
 View Solution
View SolutionQuestion 21
A plane monochromatic light wave falls normally on an opaque screen with a long slit whose shape is shown in Fig. Making use of Fig. find the ratio of intensities of light at points 1,2 and 3 located behind the screen at equal distances from it. For point 3 the rounded-off edge of the slit coincides with the boundary line of the first Fresnel zone.

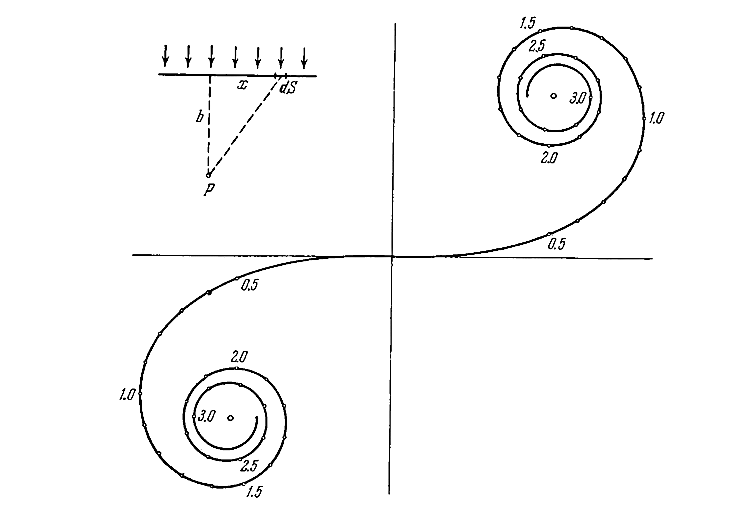 View Solution
View SolutionQuestion 22
A plane monochromatic light wave falls normally on an opaque screen shaped as a long strip with a round hole in the middle. For the observation point P the hole corresponds to half the Fresnel zone, with the hole diameter being η=1.07 times less then the width of the strip. Using Fig. find the intensity of light at the point P provided that the intensity of the incident light is equal to I0.
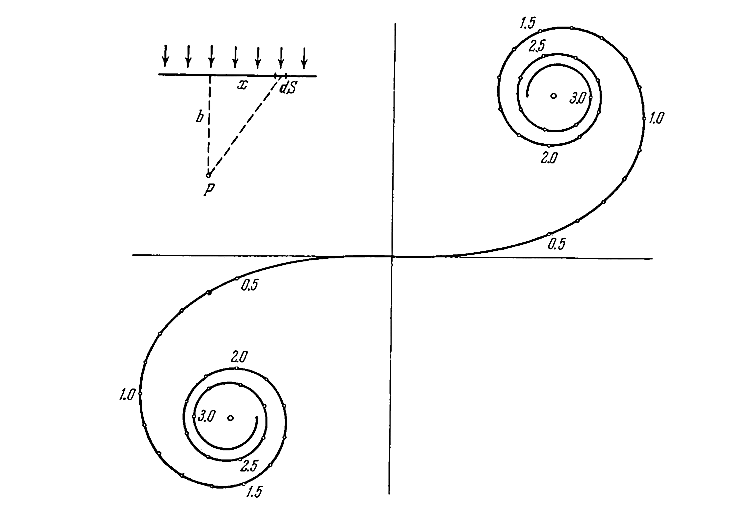 View Solution
View SolutionQuestion 26
A plane light wave with wavelength λ=0.60μm falls normally on the face of a glass wedge with refracting angle Θ=15∘. The opposite face of the wedge is opaque and has a slit of width b=10μm parallel to the edge. Final:
(a) the angle Δθbetween the direction to the Fqaunhofer maximum of zeroth order and that of incident light,
(b) the angular width of the frqunhofer maximum of the zeroth order.View SolutionQuestion 32
Light with wavelength 530nm falls on a transparent diffraction grating with period 1.50μm. Find the angle, relative to the grating normal. At which the Fraunhofer maximum of highest order is observed provided the light falls on the grating
(a) at right angles,
(b) at the angle 60∘ to the normal.View SolutionQuestion 33
Light with wavelength λ=0.60μm falls normally on a diffraction grating inscribed on a plane surfcae of a plano-curvex cylinderical glass lens with curvature radius R=20cm. The period of the grating is equal to d=6.0μm. Find the distance between the principle maxima of first order located symmetrically in the focal plane of that lens.View SolutionQuestion 34
A plane light wave with wavelength λ=0.50μm falls normally on the face of a glass wedge with an angle Θ=30∘. On the opposite face of the wedge a transparent diffraction grating with period, d=2.00μm is inscibed, whose lines are parallel to the wedge's edge. Find the angles that the direction of incident light froms with the directions to the principle Fraunhofer maxima of the zero and the first order. waht is the highest order of the spectrum? At what angle to the direction of incident light of the observed?View SolutionQuestion 35
A plane light wave with wavelength λ falls normally on a phase diffraction grating whose side view is shown in Fig. The grating is cut on a glass plate with refractive index n. Find the depth h of the lines at which the intensity of the central Fraunhofer maximum is equal to zero. what is in this case the diffraction angle corresponding to the first maximum?
 View Solution
View SolutionQuestion 36
Figure illustrates an arrangement employed in observations of diffraction of light by ultrasound. A plate light wave with wavelength λ=0.55μm passes through the water-filled tank T in which a standing ultrasonic wave is sustained at a frequency v=4.7MHz. As a result of diffraction of light by the optically inhomogemeous periodic structure a diffraction spectrum can be observed in the foacl plane of the objective O with focal length f=35cm. The separation between neighbouring maxima is Δx=0.60mm. Find the propegation velocity of ultrasonic oscillations in water.
 View Solution
View SolutionQuestion 37
To measure the angular diostance ψ between the components of a double star by Michelson's method, in front of a telescope's lens a diaphram was placeed, which has two narrow parallel slits separated by an adjustable disatnce d. While diminishing d, the first smearing of the pattern was observed in the focal plane of the objective at d=95cm. Find ψ, assuming the wavelength of light to be equal to λ=0.55μm.View SolutionQuestion 38
A transparent diffraction grating has a period d=1.50μm. Find the angular disperison D (in angular minutes per nanometers) corresponding to the maximum of highest order for a spectral line of wavelength λ=530mm of light falling on the grating
(a) at right angles,
(b) at the angle θ0=45∘ to the normal.View SolutionQuestion 44
Light falls normally on a transparent diffraction grating of width l=6.5cm with 200 lines per millimetre. The spectrum under inverstigation includes a spectral line with λ=670.8nm consisting of two components differing by δλ=0.015nm. Find:
(a) in what order of the spectrum these components will be resolved,
(b) the least difference of wavelength that can be resolved by this grating in a wavelength region λ≈670nm.View SolutionQuestion 45
With light falling normally on a transparent diffraction grating 10mm wide, it was found that the components of the yellow line of sodium (589.0 and 589.6nm) are resolved beginning with the fifth order of the spectrum. Evaluate:
(a) the period of this grating,
(b) what must be the width of the grating with the same period for a double λ=460.0nm whose components differ by 0.13nm to be resolved in the third order of the spectrum.View SolutionQuestion 46
A transparent diffraction grating of a quartz spectrograph is 25mm wide and has 250 lines per millimetre. The focal length of an objective in whose focal plane a photographic plate is located is equal to 80cm. Light falls on the grating at right angles. The spectrum under investigating includes a doublet with components of wavelength 310.154 and 310.184nm. Determine:
(a) the disatnce on the photographic plate between the components of this doublet in the spectra of the first and the second order,
(b) whether these components will be resolved in these orders of the spectrum.View SolutionQuestion 47
The ultimate resolving power λ/δλ of the spectrograph's trihedral prism is determined by diffraction of light at the prism edges (as in the case of a slit). When the prism is oriented to the least deviation angle in accordance with Rayleigh's criterion,
λ/δλ=b|dn/dλ|,
where b is the width of the prism's base (Fig.) and dn/dλ is the dispersion of its material. Derive this formula.
 View Solution
View SolutionQuestion 48
A spectrograph's trihedral prism is manufactured from glass whose refractive index varies with wavelength as n=A+B/λ2, where A and B are constats, with B being equal to 0.010μm2. Making use of the formula from the foregoing problem, find:
(a) how the resolving power of the prism depends on λ, calculate the value of λ/δλ in the vicinity of λ1=434nm and λ2=656nm if the width of the prism's base is b=5.0cm,
(b) the width of the prism's base capacble of resolving the yellow doublet of sodium (589.0 and 589.6nm). View SolutionQuestion 56
A beam of X-rays with wavelength λ=40± falls normally on aplne rectangular array of scattering centres and produces a system of diffraction maxima (Fig.) on a plane screen removed from the array by a distance l=10cm. Find the array periods a and b along the x and y axes if the distance between symmetrically located maxima of second order are equal to Δx=60mm (along the x axis) and Δy=40mm (along the yaxis).
 View Solution
View SolutionQuestion 57
A beam of X-rays impinges on a three-dimensional rectangular array whose periods are a,b, and c. The direction of the incident beam coincides with the direction along which the array period is equal to a. Find the directions to the diffraction maxima and the wavelength at which these maxima will be observed.View SolutionQuestion 59
A beam of X−rays with wavelength λ=174± falls on the surface of a single crystal rotating about its axis which is parallel let to its surface and perpendicular to the direction of the incident beam. In this case the direction to the maxima of second and third order from the system of planes parallel to the surface of the single crystal from an angle α=60∘ between them. Find the corresponding interplanar disatnce.View SolutionQuestion 60
On transmitting a bem of Xrays with wavelength λ=17.8± through a polycrystalline specimen a system of diffraction rings is produced on a screen located at a distance l=45 cm fom the specimen. Determine the radius of the bright rind corresponding to second order of reflection from the system of planes with interplanar distance d=155±View Solution