A point source of light with wavelength λ=0.50μm is located at a disatnce a=100cm in front of a diaphragm with round aperture of radius r=1.0mm. Find the distance b between the diaphragm and the observation point for which the number of Fresnel zones in the aperture equals k=3.
By definition
r2k=kabλa+b
for the periphery of the Kth zone. Then
ar2k+br2k=kabλ
So b=ar2kkaλ−r2k=ar2kaλ−r2=2 metre.
on putting the values.(It is given that r=rk) for k=3.
Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Polarization Of Light
43 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Dispersion And Absorption Of Light
24 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light
33 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
An isotropic point source emits light with wavelength λ=589nm. The radiation power of the source is P=10W. Find:
(a) the mean density of the flow of photons at a distance r=2.0m from the osurce,
(b) the distance between the source and the point at which the mean concentration of photons is equal to n=100cm−3.
View SolutionAn opaque ball of diameter D=40mm is placed between a source of light with wavelength λ=0.55μm and a photographic plate. The distance between the source and the ball is equal to a=12m and that between the ball and the photographic plate is equal to b=18m. find:
(a) the image dimension y' on the plate if the transverse dimension of the source is y=6.0mm,
(b) the minimum height of irregularities, covering the surface of the ball at random, at which the ball obstructs light.
Note: As calculations and experience shown, that happens when the height of irregularities is comparable with the width of the Fresnel zone along which the edge of an opaque screen passes.
View SolutionA lens of diameter 5.0cm and focal length f=25.0cm was cut along the diameter into two identical halves. In the process, the layer of the lens α=1.00mm in thieckness was lost. Then the halves were put together to form a composite lens. In this focal plane a narrow slit was placed, emitting monochromatic light with wavelength λ=0.60μm. Behind the lens a screen was located at a distance b=50cm from it. Find:
(a) the which of a fringe on the screen and the number of possible maxima,
(b) the maximum width of the slit ∂max at which the fringes on the screen will be still observed sufficiently sharp.
View SolutionA point source of monochromatic light is positioned in front of a zone plate at a distance a=1.5m from it. The image of the source is formed at a distance b=1.0m from the plate. Find the focal length of the zone plate.
View SolutionA plane light wave with wavelength λ=0.60μm falls normally on a sufficiently large glass plate having a round recess on the oppiste side (Fig.) For the observation point P that recess correcponds to the first one and and a half Fresnel zones. Find the depth h of the recess at which the intensity of light at the point P is
(a) maximum,
(b) minimum,
(c ) equal to the intensity of incident light.
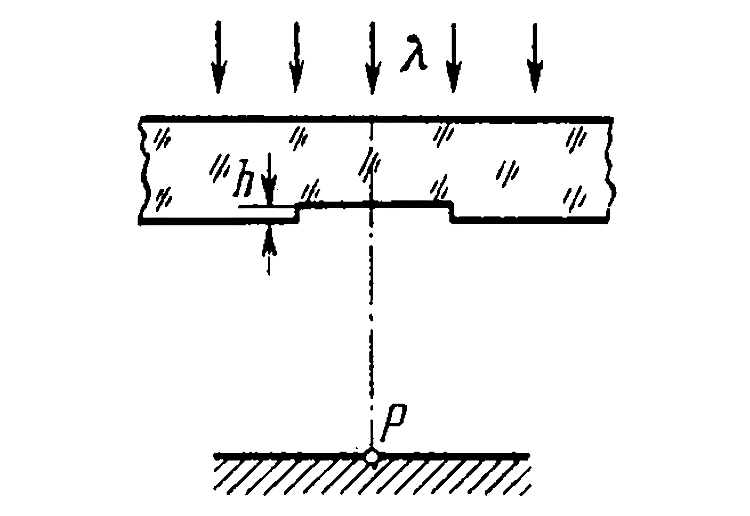
View SolutionLight with wavelength λ=0.50μm falls on a slit of width b=10μm at an angle θ0=30∘ to its normal. Find the angular position of the first minima located on both sides of the central Fraunhofer maximum.
View SolutionAn isotropic popint source emits light with wavelength 589 nm. The radiation power of the source is P = 10 W.
(a) Find the number of photons passing through unit area per second at a distance of 2 m from the source
(b) Also calculate the distance between the source and the point at which the mean concentration of the photons is 100/cm3 .
View SolutionA plane light wave with wavelength λ and intensity I0 falls normally on a large glass plate whose opposite side serves as an opaque screen with a round aperture equal to the first Fresnel zone for the observation point P. In the middle of the aperture there is a round recess equal to half the Fresnel zone. What must the depth h of that recess be for the intensity of light at the point P to be the highest? What is this intensity equal to?
View SolutionA plane light wave with wavelength λ=0.57μm falls normally on a suface on a surface of a glass (n=1.60) disc which shuts one and a half Fresnel zones for the observation point P. What must the minimum thickness of that disc be for the intensity of light at the point P to be the highest ? Take into account the interference of light on its passing through the disc.
View SolutionA monochromatic point source(S1) is at a distance d from a screen. Another identical source (S2) is at a large distance from the screen. The two sources are on a line which is perpendicular to the screen. Sources are coherent. What is the shape of interference fringes on the screen?
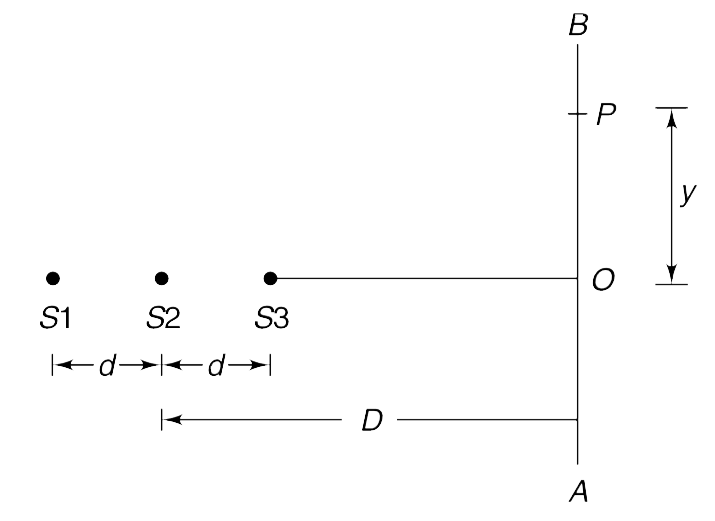
(b) Three identical coherent sources are placed on a straight line with two neighbouring ones separated by a distance d = 0.06 mm. The sources produce monochromatic light of wavelength λ = 550.4 nm. A line AB is located at a distance D = 2.50 m from the sources and is perpendicular to line joining the three sources. Intensity of light at P with any one of the sources switched on is Io. Find the intensity when all three sources are switched on. Distance of point P from O isy = 1.72 cm (see figure)
View Solution
