Section C Ncert Exemplar Solution (MCQs) from KUMAR PRAKASHAN KENDRA PHYSICS (GUJRATI ENGLISH) ELECTROMAGNETIC INDUCTION for Class 12
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC INDUCTION |
| KUMAR PRAKASHAN KENDRA PHYSICS (GUJRATI ENGLISH) | Section C Ncert Exemplar Solution (MCQs) |
| Medium | English |
| Academic Year | 2023-2024 |
Question 17
A magnetic field in a certain region is given by →B=B0cos(ωt)ˆk and a coil of radius a with resistance R is placed in the xy-plane with its centre at the origin in the magnetic field (see figure). Find the magnitude and the direction of the current at (a, 0, 0) at t=π2ω,πω and t=3π2ω. View SolutionQuestion 18
Consider a closed loop C in a magnetic field as shown in figure. The flux passing through the loop is defined by choosing a surface whose edge coincides with the loop and using the formula ϕ=→B1.d→A1+→B2.d→A2+…. Now if we choose two different surfaces S1 and S2 having C as their edge, would we get the same answer for flux. Justify your answer.View SolutionQuestion 22
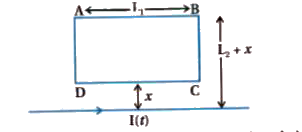
A magnetic field →B=B0sin(ωt)ˆk covers a large region where a wire AB slides smoothly over two parallel conductors separated by a distance d as in figure. The wires are in the xy-plane. The wire AB (of length d) has resistance R and the parallel wires have negligible resistance. If AB is moving with velocity v, what is the current in the circuit. What is the force needed to keep the wire moving at constant velocity ?
 View Solution
View SolutionQuestion 23
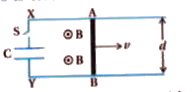
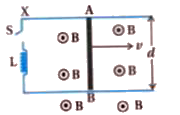
A conducting wire XY of mass m and neglibile resistance slides smoothly on two parallel conducting wires as shown in figure. The closed circuit has a resistance R due to AC. AB and CD are perfect conductors. There is a magnetic field →B=B(t)ˆk

(i) Write down equation for the acceleration of the wire XY.
(ii) If →B is independent of time, obtain v(t), assuming v (0) =u0.
(iii) For (ii), show that the decrease in kinetic energy of XY equals the heat lost in.View SolutionQuestion 24
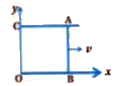
ODBAC is a fixed rectangular conductor of negligible resistance (CO is not connected) and OP is a conductor which rotates clockwise with an angular velocity ω as figure. The entire system is in a uniform magnetic field B whose direction is along the normal to the surface of the rectangular conductor ABDC. The conductor OP is in electric contact with ABDC. The rotating conductor has a resistance of λ per unit length. Find the current in the rotating conductor, as it rotates by 180∘.
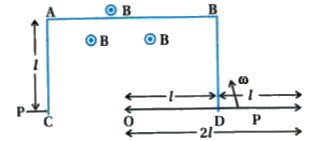 View Solution
View SolutionQuestion 27
A magnetic field B is confined to a region r≤a and points out of the paper (the z-axis), r = 0 being the centre of the circular region. A charged ring (charge Q) of radius b, b > a and mass m lies in the xy-plane with its centre at the origin. The ring is free to rotate and is at rest. The magnetic field is brought to zero in time Δt. Find the angular velocity ω of the ring after the field vanishes.View SolutionQuestion 28
A rod of mass m and resistance R slides smoothly over two parallel conducting wires kept sloping at an angle θ with respect to the horizontal as shown in figure. The circuit is closed through a perfect conductor at the top. There is a constant magnetic field →B along the vertical direction. If the rod is initially at rest, find the velocity of the rod as a function of time.
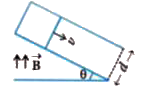 View Solution
View SolutionQuestion 31
A metallic ring of mass m and radius l (ring being horizontal) is falling under gravity in a region having a magnetic field. If z is the vertical direction, the z-component of magnetic field is BZ=BO(I+λz). If R is the resistance of the ring and if the ring falls with a velocity v, find the energy lost in the resistance. If the ring has reached a constant velocity, use the conservation of energy to determine v in terms of m, B, λ and acceleration due to gravity g.View SolutionQuestion 32
A long solenoid 'S' has 'n' turns per meter, with diameter 'a'. At the centre of this coil we place a smaller coil of 'N' turns and diameter 'b' (where b < a). If the current in the solenoid increases linearly, with time, what is the induced emf appearing in the smaller coil. Plot graph showing nature of variation in emf, if current varies as a function of mt2+C. View Solution
All Exercises from KUMAR PRAKASHAN KENDRA PHYSICS (GUJRATI ENGLISH) Class 12 PHYSICS ELECTROMAGNETIC INDUCTION
- SECTION A (QUESTION & ANSWER)
- SECTION A (TRY YOURSELF )
- SECTION A HOTS
- SECTION B (NUMERICAL) NUMERICAL FROM DARPAN BASED ON TEXTBOOK
- SECTION B (NUMERICAL) NUMERICAL FROM TEXTUAL EXERCISE
- SECTION B (NUMERICAL) TEXTUAL ILLUSTRATIONS
- SECTION C NCERT EXEMPLAR SOLUTION (LONG ANSWER )
- SECTION C NCERT EXEMPLAR SOLUTION (MCQS)
- SECTION C NCERT EXEMPLAR SOLUTION (SHORT ANSWER )
- SECTION D MCQS (MCQS ASKED IN COMPETITIVE EXAMS )
- SECTION D MCQS (FROM DARPAN BASED ON TEXTBOOK )