SAMPLE PROBLEM from RESNICK AND HALLIDAY PHYSICS (HINGLISH) CIRCULAR MOTION for Class 12
| Class 12 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| RESNICK AND HALLIDAY PHYSICS (HINGLISH) | SAMPLE PROBLEM |
| Medium | English |
| Academic Year | 2023-2024 |
Question 2
IAF fighter pilots have long worried about taking a turn too tightly. As a pilot's body undergoes centripetal acceleration, with the head toward the center of curvature, the blood pressure in the brain decreases, leading to loss of brain function.
There are several warning signs. When the centripetal acceleration is 2g or 3g, the pilot feels heavy. At about 4g, the pilot's vision switches to black and white and narrows to tunnel vision. If that acceleration is sustained or increased, vision ceases adn, soon after, the pilot is unconscious a condition known as g-LOC for g-induced loss of consciousness.
What is the magnitude of the acceleration in g units, of a pilot whose aircraft enters a horizontal circular turn with a velocity of ¯vati=(400ˆi+300ˆj) m/s and 25 s later leaves the turn with a velocity of ¯vˆj=(−400ˆi−300ˆj) m/s? Assume speed is constant.View SolutionQuestion 4
Largely because of riding in cars, you are used to horizontal circular motion. Vertical circular motion would be a novelty. In this sample problem, such motion seems to defy the gravitational force.
In a 1901 circus performance, Allo Dare Devil Diavolo introduced the stunt of riding a bicycle in a loop the loop. Assuming that the loop is a circle with radius R=2.7m, what is the least speed v that Diavolo and hisbicycle could have at the top of the loop to remain in contact with it there?View SolutionQuestion 5
Even some seasoned roller coaster riders blanch at the thought of riding the Rotor, which is essentially a large, hollow cylinder that is rotated rapidly around its central axis. Before the ride begins, a rider enters the cylinder through a door on the side and stands on a floor, up against a canvas covered wall. The door is closed, and as the cylinder begins to turn, the rider, wall, and floor move in unison. When the rider's speed reaches some predetermined value, the floor abruptly and alarminglly falls away. The rider does not fal with it but instead is pinned to the wall while the cylinder rotates, as if an unseen (and somewhat unfriendly) agent is pressin the body to the wall. Later, the floor is eased back to the rider's feet, the cylinder slows. and the rider sinks a few centimeters to regain footing on the floor. (Some riders consider all this to be fun.)
Suppose that the coefficient of static friction μs between the rider's clothing and the canvas is 0.40 and that the cylinder's radius R is 2.1 m.
a. What minimum speed v must the cylinder and rider have if the rider is not to fall when the floor drops?
b. If the rider's mass is 49 kg, what is the magnitude of the centripetal force on her?View SolutionQuestion 6
Upside down racing: A modern race car is designed so that the passing air pushes down on it, allowing the car to travel much faster through a flat turn in a Grand Prix without friction failing. This downward push is called negative lift. Can a race can have so muchh negative lift it could be driven upside won on a long ceiling, as done fictionally by a sedan in the first Men in Black movie?
Figure represents a Grand Prix race car of mass m=600 kg as it travels on a flat in a circular arc of radius R=100m. Becuase of the shape of the car and the wings on it, passing air exerts a negative lift →FL
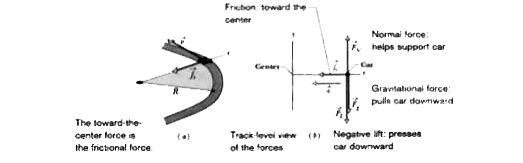
downward on the car. The coefficient of static friction between the tires and the track is 0.75. (Assume that the forces on the four tires are identical).
a. If the car is on the verge of sliding out of the turn when its speed is 28.6 m/s what is the magnitude of the negative lift →FL, acting downward on the car?
b. The magnitude FL of the negative lift on a car depends on the square of the car's speed v2, just as the drag force does. Thus the negative lift on the car here is greater when the car travels faster, as it does on a straight section of track. What is the magnitude of the negative lift for a speed of 90 m/s?View SolutionQuestion 8
This problem is quite challenging in setting up but takes only a few of algebra to solve. We deal with not only uniformly circular motion but also a ramp. However we will not need a tilted coordinate system as with other ramps. Insttead we can take a freeze frame of the motion and work with simply horizontaly and vertical axes. As always in this chapter, the starting point will be to apply Newton's second law, but that will required us to identify the force component that is responsible for the uniform circular motion.
Curved portions of highways. are always banked (tilted) to prevent cars from sliding off the highway. When a highway is dry, the frictional force between the tires and the road surface may be enough to prevent sliding. When the highway is wet, however, the frictional force may be neglifible, and baking is then essential. fig represents a car of mass m as it moves at a constant speed v to 20m/s around a banked circular track of radius R=190m. (It is a normal car, rather than a race car, which meas that any vertical force from the passing air is negligible). If the frictional force from the track is negligible, what bank angle θ prevents sliding?View Solution