The triangular prism shown in Figure I above has index of refraction 1.5 and angles of 37° 53° and 90°.The shortest side of the prism is set on a horizontal table. A beam of light initially horizontal is incident on the prism from the left.a. On Figure I above sketch the path of the beam as it passes through and emerges from the prism.b. Determine the angle with respect to the horizontal angle of deviation of the beam as it emerges from the prism.c. The prism is replaced by a new prism of the same shape which is set in the same position. The beam experiences total internal reflection at the right surface of this prism. What is the minimum possible index of refraction of this prism?The new prism having the index of refraction found in part c is then completely submerged in water index of refraction = 1.33 as shown in Figure II below. A horizontal beam of light is again incident from the left.d. On Figure II sketch the path of the beam as it passes through and emerges from the prism.e. Determine the angle with respect to the horizontal angle of deviation of the beam as it emerges from the prism.
ab ni sin θi = nr sin θr … 1.5 sin 37 = 1 sin θr θr = 65° … therefore angle α shown above is 28°.c ni sin θi = nr sin θr … ni sin 37 = 1 ni = 1.66 any n higher than this causes total internal.d This ray would not totally reflect because by putting it in water we have reduced the difference between the n’s meaning less bending and the limit of total internal has not be reached.e ni sin θi = nr sin θr … 1.66 sin 37 = 1.33 sin θr … θr = 48.7° – 37° = 11.7°
Related Solutions
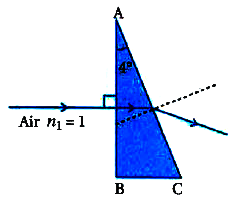
A horizontal ray is incident on a right-angled prism with prism angle of 4o. If the refractive index of material of the prism is 1.5, angle of emergence is .......... . Use the given figure.
View Solutionचित्र में दिखाए अनुसार काँच के प्रिज्म ABC में प्रकाश का किरण पथ खींचिए।यदि काँच का अपवर्तनांक हो तो प्रिज्म से निर्गत कोण का मान ज्ञात कीजिए।

View Solutionप्रिज्म के किसी अपवर्तनांक पृष्ठ पर पोइ प्रकाश किरण आपतन कोण पर गिरती है। प्रिज्म का कोण है। यदि यह किरण प्रिज्म से न्यूनतम विचलित होती है तो न्यूनतम विचलन कोण तथा प्रिज्म के पदार्थ का अपवर्तनांक क्रमशः है :
View SolutionIn the above figure a narrow beam of white light is shown to pass through a triangular glass prism. After passing through the prism, it produces a spectrum XY on a screen. State the colour seen at (i) X and (ii) Y.
View SolutionIn a prism of small angle A, a beam of light is incident on its surface at an angle of incidence i and leaves the opposite surface of it is angle of with the surface. If prism material has refractive index of m then the value of angle of incidence will be:
View SolutionA ray of light passes through an equilateral prism in such a way that the angle of incidence is equal to the angle of emergence and each of these angles is th the angle of the prism. Determine the (i) angle of deviation and (ii) the refractive index of the prism.
View SolutionA glass prism has refractive index and refracting angle . One of the refracting surface of the prism is silvered. A beam of monchromatic light will retrace it path it its angle of incidence on the unsilvered refracting surface of the prism is
View SolutionA glass prism has refractive index sqrt(2) and refracting angle 30^(@) . One of the refracting surface of the prism is silvered. A beam of monchromatic light will retrace it path it its angle of incidence on the unsilvered refracting surface of the prism is
View SolutionFigure shows the path of a light beam in an isosceles prism with apex angle (inside the prism beam is parallel to the base). Find the angle of deflection in degrees. The refractive index of prism material is

View Solutionएक समकोणीय समद्विबाहु प्रिज्म पर एक प्रकाश किरण अभिलंबवत आपतित होती है (चित्रानुसार), तो प्रिज्म के अपवर्तनांक का न्यूनतम मान होना चाहिए
View SolutionA ray of light is incident on the glass prism at an angle of 40^(@) . Find the angle of emergence, if the angle of prism is 60^(@) and refractive index is 1.5.
View SolutionA prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. The angle of minimum deviation is measured to be 40°. What is the refractive index of the material of the prism? The refracting angle of the prism is 60°. If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light.
View SolutionA prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. The angle of minimum deviation is measured to be . What is the refractive index of the material of the prism? The refracting angle of the prism is . If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light
View SolutionA prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. The angle of minimum deviation is measured to be . What is the refractive index of the material of the prism? The refracting angle of the prism is . If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light
View SolutionA prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. The angle of minimum deviation is measured to be 40^(@) . What is the refractive index of the materal of the prism? The refracting angle of the prism is 60^(@) . If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of parallel beam of light.
View SolutionA prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. The angle of minimum deviation is measured to be . What is the refractive index of the material of the prism? The refracting angle of the prism is . If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light.
View SolutionA prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. The angle of minimum deviation is measured to be 40^(@) . What is the refractive index of the material of the prism? The refracting angle of the prism is 60^(@) . If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light
View SolutionA ray of light passes through an equilateral glass prism such that angle of incidence (i) is equal to angle of emergence (e). If angle of emergence (e) is (3/4) times the angle of prism (A). Calculate the refractive index of glass prism.
View SolutionThe angle of minimum deviation from a prism is . If the angle of prism is , find the refractive index of the material of the prism.
View SolutionThe angle of minimum deviation from a prism is . If the angle of prism is , find the refractive index of the material of the prism.
View Solution