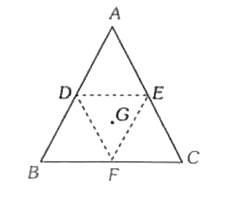
An equilateral triangle ABC is cut from a thin solid sheet of wood. See figure D E and F are the mid-points of its sides as shown and G is the centre of the triangle. The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane of the triangle is I0. If the smaller triangle DEF is removed from ABC the moment of inertia of the remaining figure about the same axis is I. Then :
The correct option is 4.Explanation:
Related Solutions
An equilateral triangle ABC is cut from a thin solid sheet of wood .(see figure ) D,E and F are the mid-points of its sides as shown and G is the centre of the triangle.The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane to the triangle is I_(0) If the smaller triangle DEF is removed from ABC , the moment of inertia of the remaining figure about the same axis is I. Then :
View SolutionAn equilateral triangle ABC is cut from a thin solid sheet of wood .(see figure ) D,E and F are the mid-points of its sides as shown and G is the centre of the triangle.The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane to the triangle is If the smaller triangle DEF is removed from ABC , the moment of inertia of the remaining figure about the same axis is I. Then :

View SolutionAn equilateral triangle ABC is cut from a thin solid sheet of wood. (See figure) D, E and F are the mid-points of its sides as shown and G is the centroid of the triangle. The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane of the triangle I_0 Is. If the smaller triangle DEF is dropped from ABC, then the moment of inertia of the rest of the figure about the same axis is I. Then:
View Solutionएक पतले ठोस लकड़ी के फलक से एक त्रिभुज ABC काटा गया हैं (चित्र देखिए) दर्शाए गये अनुसार D, E तथा F इसकी भुजाओं के मध्य बिन्दु हैं तथा G त्रिभुज का केन्द्र है। G से गुजरने वाली तथा त्रिभुज के समतल के लम्बवत् अक्ष के सापेक्ष त्रिभुज का जडत्व आघूर्ण है। यदि छोटा त्रिभुज DEF त्रिभुज ABC में से निकाल लिया जाये तो शेष बचे हुए भाग का उसी अक्ष के सापेक्ष जडत्व आघूर्ण है। तब
View SolutionIf D, E and F are the mid-points of the sides of an equilateral triangle ABC, then the ratio of the area of triangle DEF and DCF is :
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral ABC. Show that DEF is also an equilateral triangle.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of and equilateral ABC. Show that DEF is also an equilateral triangle.
View SolutionIn Figure, and are, respectively the mid-points of sides and of an equilateral triangle . Prove that is also an equilateral triangle.
View SolutionThe mid-points of the sides of an equilateral triangle ABC are DE and F. triangle DEF and triangle The ratio of the areas of the DCF will be
View SolutionD,E and F are respectively the mid points of the sides BC,CA and AB of an equilateral triangle ABC, prove that DEF is also equilateral triangle.
View SolutionD, E and F are respectively the mid-points of sides AB, BC and CA of . Find the ratio of the areas of .
View SolutionIn are respectively the mid points of the sides AB, BC and AC. Find ratio of the area of and area of .
View SolutionD,E,F are the mid points of the sides BC, CA and AB respectively of a . Determine the ratio of the areas of and .
View SolutionIf D, E and F are the mid-points of sides BC, CA and AB respectively of , then the ratio of the areas of to the area of is :
View SolutionD, E, F are mid points of sides BC, CA, AB of . Find the ratio of areas of .
View SolutionD, E, F are mid points of sides BC, CA, AB of . Find the ratio of areas of .
View SolutionD, E, F are mid points of sides BC, CA, AB of . Find the ratio of areas of .
View SolutionIn trigle ABC, the points D, E, F are the midpoints of the sides BC,CA, and AB respee. Tively. Using vector methed ,show that the area of DEF is equal to (area of ABC).
View Solutionలో AB,BC మరియు CA భుజాల మద్య బిందువులు వరుసగా D, E మరియు F లు అయిన =
View Solution