A simple pendulum is suspended from a peg on a vertical wall. The pendulum is pulled away from the wall to a horizontal position Fig. 1.19 and released. The ball hits the wall the coefficient of restitution being 2/√5 . What is the minimum number of collisions after which the amplitude of oscillation becomes less than 60°?
Let v0 be the velocity of the bob just before the first collision.The velocity of the bob just after the 1st collision isv1 will be the velocity of the bob just before 2nd collision. The velocity of the bob just after the second collision isThe velocity just after the nth collision isWe assume that after n collisions the amplitude of oscillation becomes 60°. n is slightly greater than 3. In factThus the minimum number of collisions after which the amplitude becomes less than 60° is 4.
Related Solutions
A simple pendulum is supended from a peg on a verticl wall. The pendulum is pulled away from the wall to a horizontal position and releases as shown in figure The ball hits the wall, the coefficient of restitution being What is the minimum number of collisions after which the amplitude of oscillation becomes less than
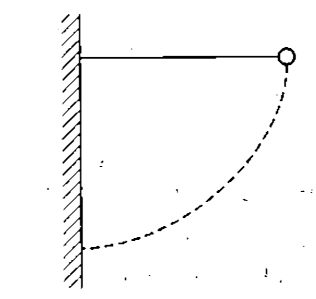
View Solutionएक सरल लोलक खूँटी (Peg) की सहायता से ऊर्ध्वाघर दीवार पर लटकाया गंया है। लोलक को खींचकर चित्रानुसार दीवार से दूर क्षैतिज स्थिति में लाया जाता है तथा छोड़ दिया जाता है। गोलक दीवार से टकराता है, यदि प्रत्यावस्थान गुणांक (Coefficient of restitution) , हो, तो संघट्टों की कम-से-कम कितनी संख्या होगी, जिनके बाद दोलनों का आयाम से कम रह जाएगा?
View SolutionFrom a rod fixed on a vertical wall, a simple pendulum is suspended. Its bob is pulled away from the wall to a horizontal position and then released. If the coefficient of restitution is 2/sqrt(5) , what would be the minimum number of impacts of the bob with the wall, after which the amplitude of the pendulum becomes less than 60^@ ?
View SolutionA simple pendulum is suspended from a peg on a wall which is inclined at an angle of 30^(@) with the vertical. The pendulum is pulled away from the wall to a horizontal position (with string just taut) and released. The bob repeatedly bounces off the wall, the coefficient of restitution being e = (2)/(sqrt(5)) Find the number of collisions of the bob with the wall, after which the amplitude of oscillation (meaured from the wall) becomes less than 30^(@)
View SolutionA simple pendulum is hanging from a per inserted in a vertical wall. Its bob is stretched to horizontal position from wall and is left free to move, the bob hits the wall. If coefficient of restitution is (2)/(sqrt(5)) . After how many collisions the amplitude of vibration will become less than 60^(@)
View SolutionA simple pendulum is hanging from a per inserted in a vertical wall. Its bob is stretched to horizontal position from wall and is left free to move, the bob hits the wall. If coefficient of restitution is . After how many collisions the amplitude of vibration will become less than
View SolutionA simple pendulum is hanging from a peg inserted in a vertical wall. Its bob is stretched in horizontal position from the wall and is left free to move. The bob hits on the wall the coefficient of restitution After how many collsions the amplitude of vibration will become less than
View SolutionA simple pendulum is hanging from a peginserted in a vertical wall. Its bob is strteched to horizontal position form wall and left freee to move, the bob hits the wall. If coefficient of restitution is (2)/(sqrt(5)) . After how many collisions the amplitude of vibration will becomes less then 60^(@) .
View SolutionA simple pendalum is suspended from a peg on a verticle wall . The pendulum is pulled away from the well is a horizental position (see fig) and released . The bell his the well the coefficient of resitution being (2)/(sqrt(5) what is the miximum number of colision after which the amplitube of secillections between less that 60 digree ?
View SolutionA simple pendalum is suspended from a peg on a verticle wall . The pendulum is pulled away from the well is a horizental position (see fig) and released . The bell his the well the coefficient of resitution being (2)/(sqrt(5) what is the miximum number of colision after which the amplitube of secillections between less that 60 digree ?
View SolutionA simple pendalum is suspended from a peg on a verticle wall . The pendulum is pulled away from the well is a horizental position (see fig) and released . The bell his the well the coefficient of resitution being (2)/(sqrt(5) what is the miximum number of colision after which the amplitube of secillections between less that 60 digree ?
View SolutionA simple pendalum is suspended from a peg on a verticle wall . The pendulum is pulled away from the well is a horizental position (see fig) and released . The bell his the well the coefficient of resitution being (2)/(sqrt(5) what is the miximum number of colision after which the amplitube of secillections between less that 60 digree ?
View SolutionA ball wall PQ which is vertical alpha Inclined at an angle, but suspended at the point by a string of length L. The string with the ball is now at a slight angle away from the vertical wall. beta If the ball is released, find the time of oscillation of the pendulum, when beta lt alpha Let the collision on the wall be perfectly elastic.
View SolutionA simple pendulum ia hanging from a per inserted in a vertical wall. Its bob is stretched to horizontal position from wall and is left free to move, the bob hits the wall. If coefficient of restitution is . After how many collision the amplitude of vibration will become less than (Hint : )
View SolutionA simple pendulum is hanging from a per inserted in a vertical wall. Its bob is stretched to horizontal position from wall and is left free to move, the bob hits the wall. If coefficient of restitution is After how many collision the amplitude of vibration will become less than 60° (Hint: )
View SolutionA ball is suspended by a thread of length L at a point O on a wall inclined at an angle a to the vertical. angle smaller than the vertical to the thread with the ball beta Displaced by 80 and also kept away from the wall. If the ball is released, what will be the time period of oscillation of the pendulum when beta gt alpha Is
View SolutionA ball is attached to a string of length L . The ball is released when the string is horizontal. The ball collides with wall and e = 2//sqrt(5) . After how many minimum number of collisions , the amplitude of oscillation becomes less than 60^(@) .
View SolutionA ball is suspended by a thread of length L at the point O on a wall which in indeed to the vertical by . The thread with the ball is displaced by a small angle away from the vertical and also away from the wall. If the ball is released, the period of observation of the pendulum when will be...........
View SolutionA small ball is projected from point P towards a vertical wall as shown in Fig. It hits the wall when its velocity is horizontal. Ball reaches point P after one bounce on the floor. The coefficient of restitution assuming it to be same for two collisions is n//2 . All surfaces are smooth. Find the value of n .
View SolutionA small ball is projected from point P towards a vertical wall as shown in Fig. It hits the wall when its velocity is horizontal. Ball reaches point P after one bounce on the floor. The coefficient of restitution assuming it to be same for two collisions is n//2 . All surfaces are smooth. Find the value of n .
View Solution