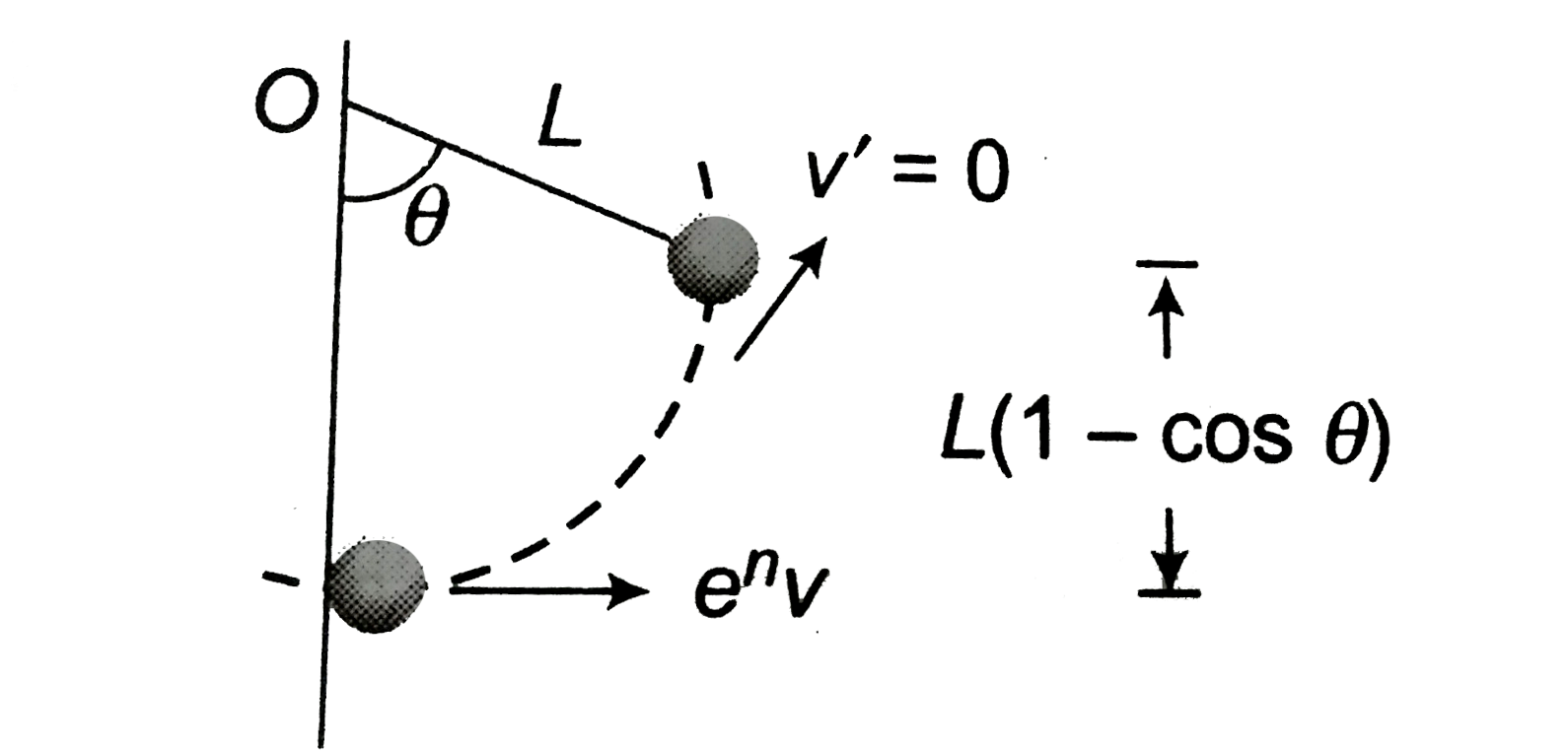
A ball is attached to a string of length L. The ball is released when the string is horizontal. The ball collides with wall and e=2/√5. After how many minimum number of collisions , the amplitude of oscillation becomes less than 60∘.

When the ball strikes the first time , its speed v=√2gL
Speed of ball after the nth collision =env
0=(env)2−2gL(1−cosθ)
=e2nv2−2gL(1−cosθ)
cosθ=1−e2n
=1−(2√5)2n=1−(45)n
If θ<60∘,cosθ>12
1−(45)n>12⇒(45)n<12
If n=1,(45)1=0.8
n=2,(45)2=0.64
n=3,(45)3=0.512
n=4,(45)4=0.41
Minimum number of collisions =4

Topper's Solved these Questions
Similar Questions
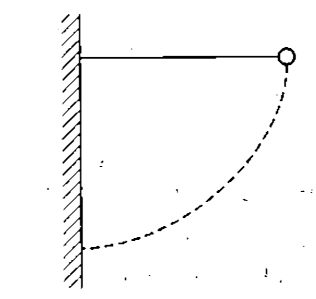
A simple pendulum is supended from a peg on a verticl wall. The pendulum is pulled away from the wall to a horizontal position and releases as shown in figure −4.152. The ball hits the wall, the coefficient of restitution being 2/√2. What is the minimum number of collisions after which the amplitude of oscillation becomes less than 60∘
 View Solution
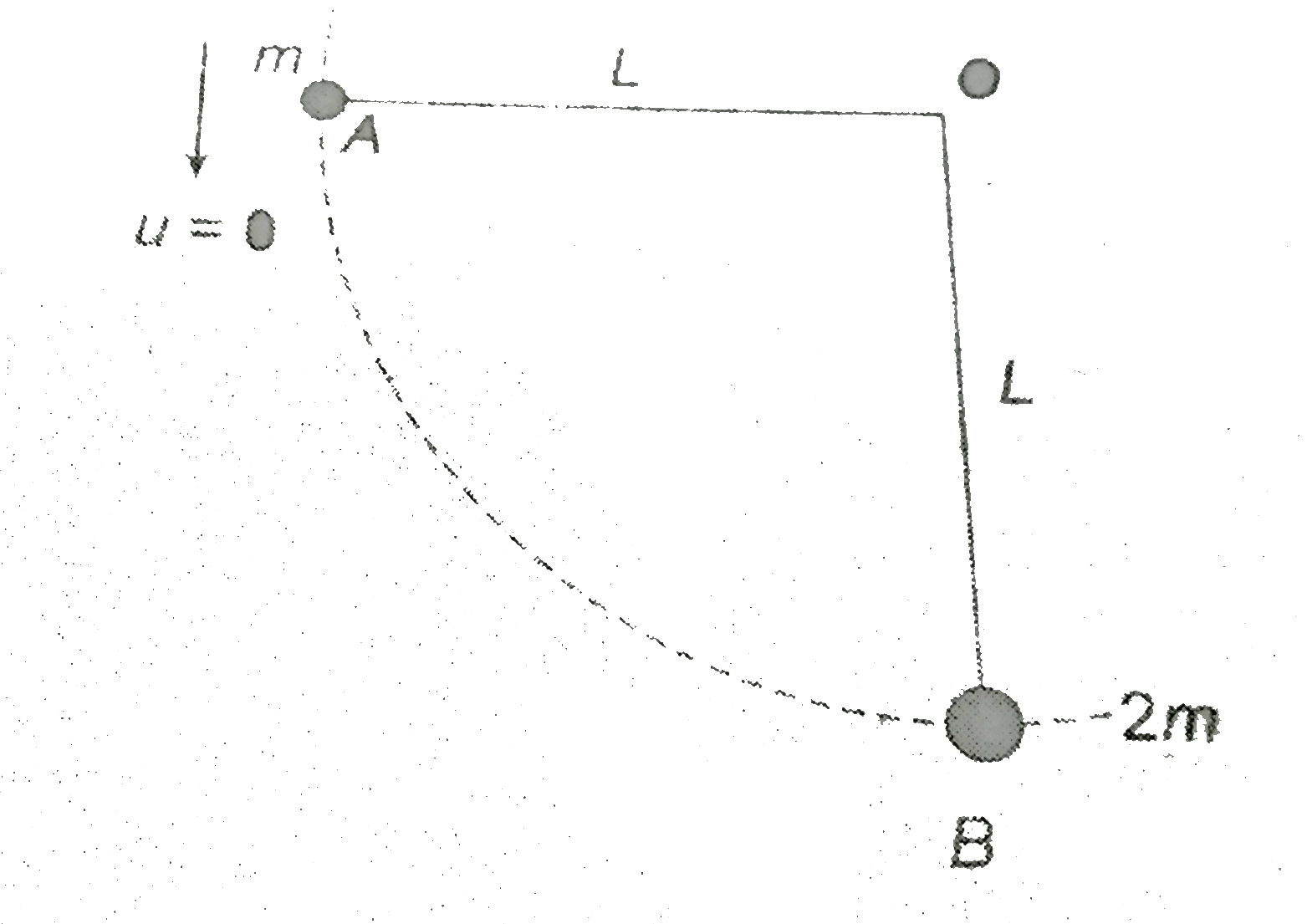
View SolutionA ball A of mass m attached to a string of length L is released when the string is horizontal. It strikes another ball B of mass 2m suspended to another string of length L at rest as shown. Find the maximum angle made by the string if the collision is completely inelastic.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The ball is released when the string is horizontal. The collision between the ball and the block is head - on elastic. The velocities of the ball and the block immediately after collision
 A23√2gL,13√2gLB−23√2gL,13√2gLC23√2gL,−13√2gLD−23√2gL,−13√2gL
A23√2gL,13√2gLB−23√2gL,13√2gLC23√2gL,−13√2gLD−23√2gL,−13√2gL - Question 2 - Select One
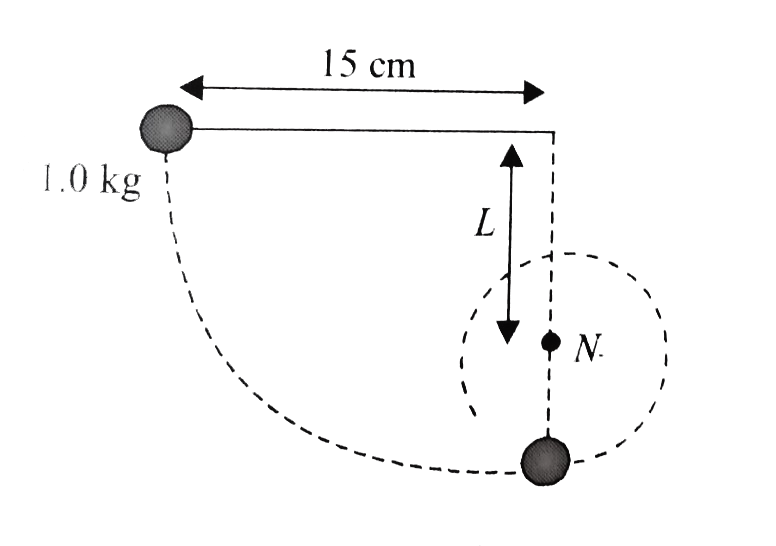
A ball weighing 1.0 kg is tied to a string 15 cm long initially the ball is held in position such that the string is horizontal. The ball is now released. A nail N is situated vertically below the support at a distance L. The minimum value of L such that the string will be would round the nail is.A15 cmB4 cmC9 cmDNone of these
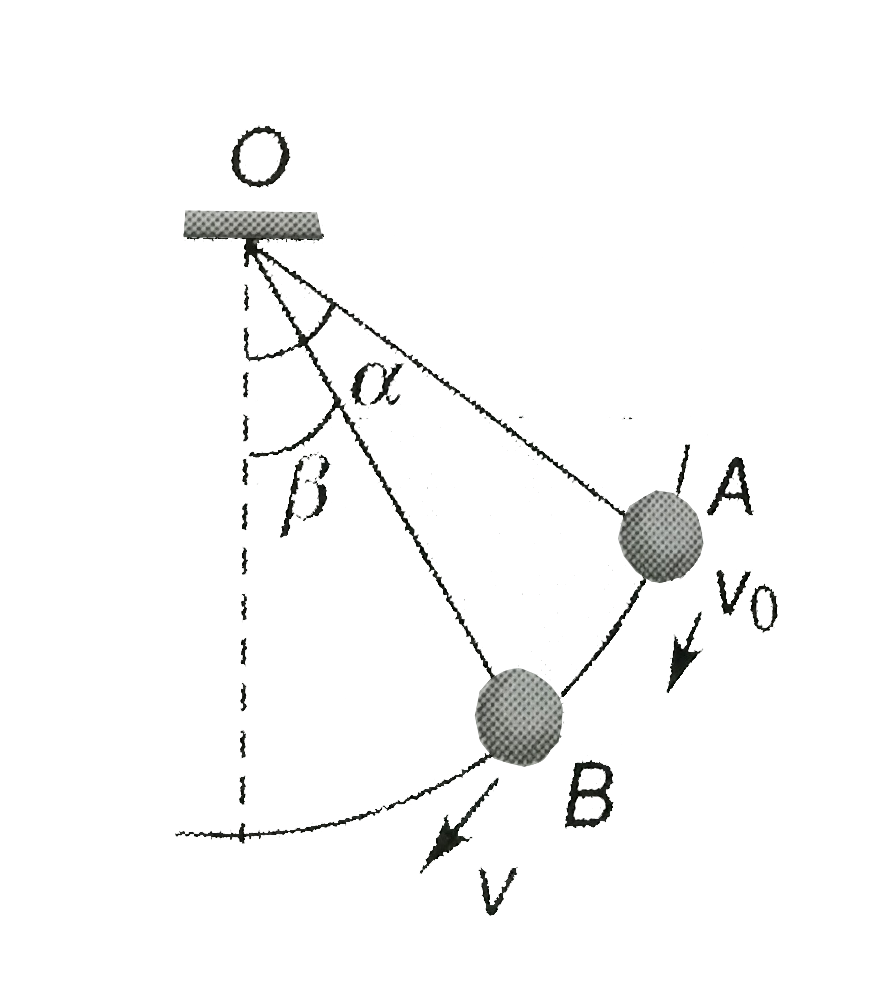
A ball attached to a string length L is oscillating line a simple pendulum. Find v in terms of v0 L α and β.View Solution
A ball is attached to a string of length L and the ball is given velocity v0 at its lowest point. Find the speed of the ball at point B,C and D. Assume that the ball is moving in vertical circle.View SolutionA simple pendulum is suspended from a peg on a wall which is inclined at an angle of 30∘ with the vertical. The pendulum is pulled away from the wall to a horizontal position (with string just taut) and released. The bob repeatedly bounces off the wall, the coefficient of restitution being e=2√5
Find the number of collisions of the bob with the wall, after which the amplitude of oscillation (meaured from the wall) becomes less than 30∘
 View Solution
View Solution
A ball weighing 1.0 kg is tied to a string 15 cm long initially the ball is held in position such that the string is horizontal. The ball is now released. A nail N is situated vertically below the support at a distance L. The minimum value of L such that the string will be would round the nail is.View SolutionA particle of mass 21 g attached to a string of 70cm length Keeping the string always taut the ball describes a horizontal circle of radius 15cm Calculate the angular speed of the ball .
View SolutionA smooth ball of mass m is suspended from a light string of length 1m. Another ball of mass 2m strikes the ball of mass in horizontally with a speed of u=√35m/s. The coefficient of restitution for the collision is e. The string becomes loose, when it makes an angle of 30∘ with the horizontal, find the value of e.
 View Solution
View Solution

