A wire frame is in the shape of a parabola y=5x^2 . It is being rotated about y axis with an angular velocity Omega. A small head of mass m=1 kg is at point P and is in equilibrium with respect to frame . Then the angular velocity Omega is
Related Solutions
A smooth wire frasme is in the shape of a parabola y = 5x^(2) . It is being rotated about y-axis with an angular velocity omega . A small bead of mass (m = 1 kg) is at point P and is in equilibrium with respect to the frame. Then the angular velocity omega is (g = 10 m//s^(2))
View SolutionA smooth wire frasme is in the shape of a parabola . It is being rotated about y-axis with an angular velocity . A small bead of mass is at point and is in equilibrium with respect to the frame. Then the angular velocity is
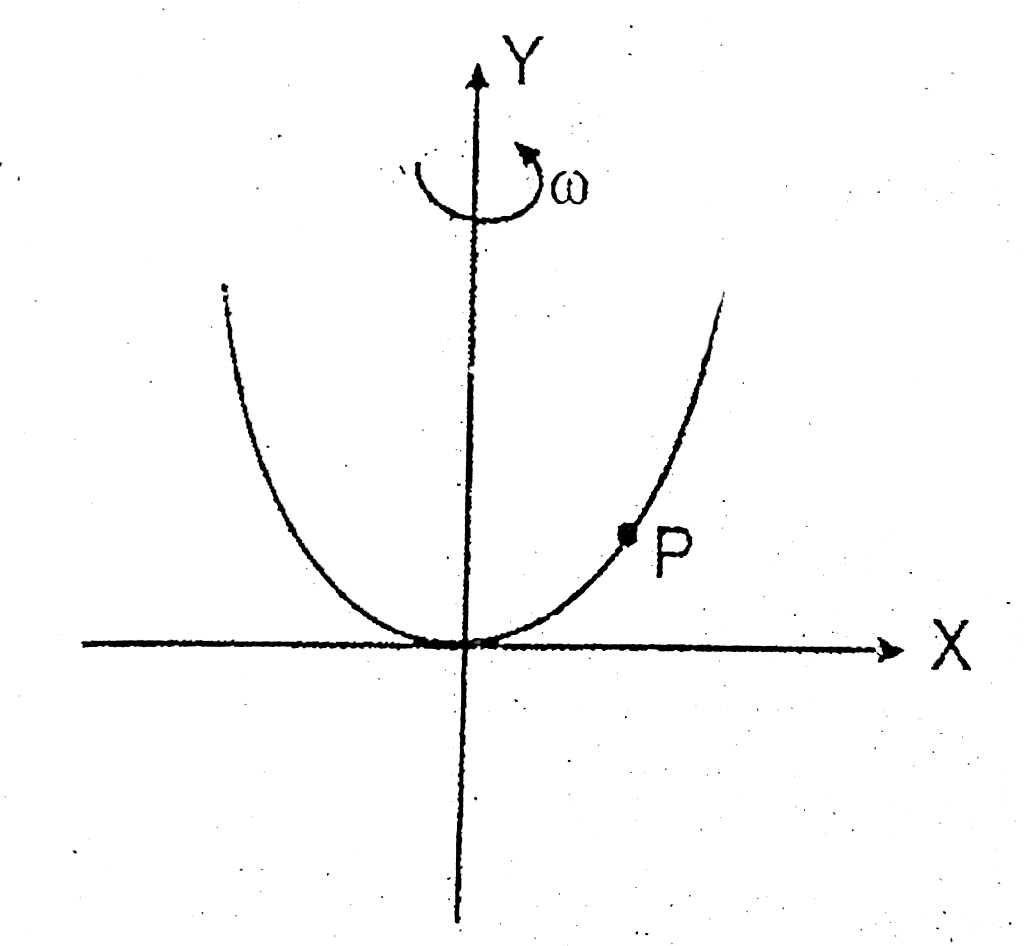 View Solution
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity . If a increases then tension in ring
View SolutionA body of mass M is rotating about an axis with angular velocity omega . If k is radius of gyration of the body about the given axis, its angular momentum is
View SolutionA bead of mass m stays at point P (a,b) on a wire bent in the shape of a parabola and rotating with angular speed (see figure ) . The value of is (neglect friction),
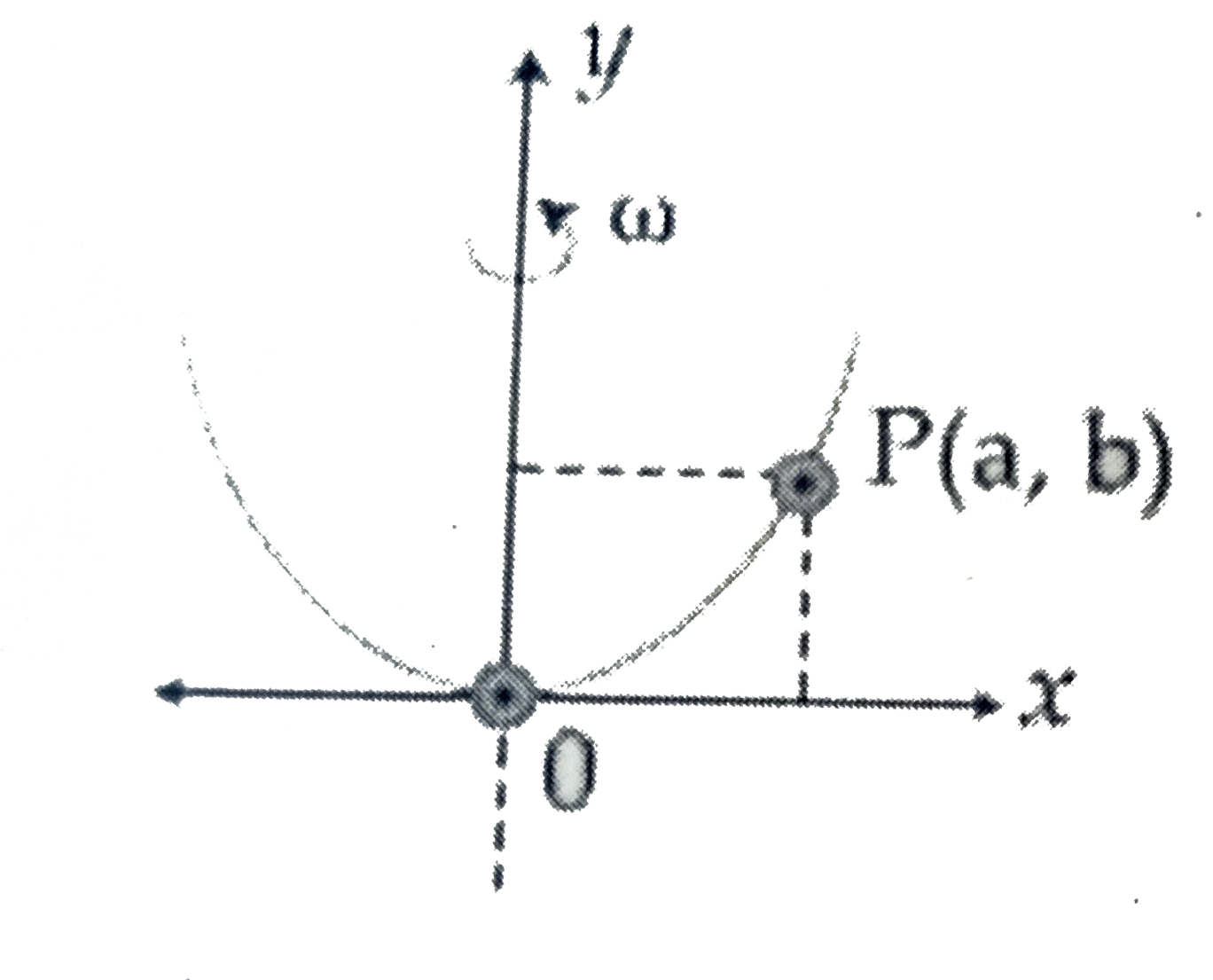 View Solution
View SolutionA bead of mass m stays at point P (a,b) on a wire bent in the shape of a parabola y =4 Cx^(2) and rotating with angular speed omega (see figure ) . The value of omega is (neglect friction),
View SolutionIf I, alpha and tau are the moment of inertia, angular acceleration and torque respectively of a body rotating about an axis with angular velocity omega then,
View SolutionIf I, alpha and tau are the moment of inertia, angular acceleration and torque respectively of a body rotating about an axis with angular velocity omega then,
View SolutionIf I, alpha and tau are MI, angular acceleration and torque respectively of a body rotating about any axis with angular velocity omega , then
View SolutionTwo identical disc are placed one over the other and both are rotating about a common axis through their centre and normal to their frame with angular velocity omega . If the upper disc is suddenly removed, angular velocity of the other disc would be
View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end wth an angular velocity . Find angular momentum of the rod about the axis rotation.View SolutionA rod of mass 2 kg ad length 2 m is rotating about its one end O with an angular velocity omega=4rad//s . Find angular momentum of the rod about the axis rotation.
View SolutionA rod is rotating with angular velocity omega about axis AB. Find costheta .
View SolutionA rod is rotating with angular velocity omega about axis AB. Find costheta .
View SolutionIf omega_(E ) is the angular velocity of the earth rotating about its own axis and omega _(H) is the angular velocity of the hour of a clock , then
View SolutionAn cylinder of mass m is rotated about its axis by an angular velocity omega and lowered gently on an inclined plane as shown in figure. Then : .
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with constant angular velocity . The objects each of mass m are attached gently to the ring. The wheel now rotates with an angular velocity.
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with constant angular velocity omega . The objects each of mass m are attached gently to the ring. The wheel now rotates with an angular velocity.
View SolutionA ring of mass m and radius R is being rotated about its axis with constant angular velocity omega in the gravity free space. Find tension in the ring.
View SolutionFour point masses are fastened to the corners of a frame of negligible mass lying in the xy plane. Let w be the angular speed of rotation. Then
View Solution
