A smooth wire frasme is in the shape of a parabola $y = 5 x^{2}$ . It is being rotated about y-axis with an angular velocity $ω$ . A small bead of mass $(m = 1 k g)$ is at point $P$ and is in equilibrium with respect to the frame. Then the angular velocity $ω$ is $(g = 10 m / s^{2})$

A

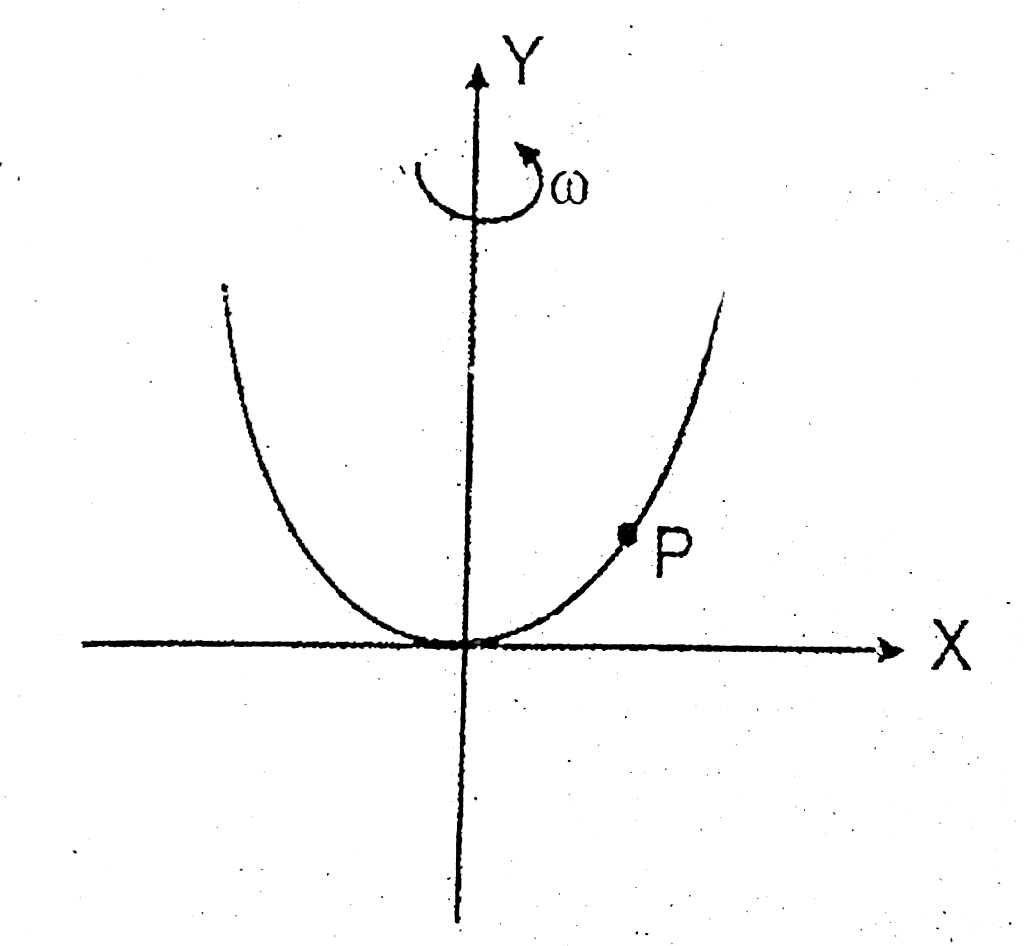
$ω = 5 r a d / sec$

B

$ω = 10 r a d / sec$

C

$ω = 20 r a d / sec$

D

Depends of x-coordinate of particle

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

A smooth wire …………

$(1) m ω^{2} x cos θ = m g sin θ \Rightarrow tan θ = \frac{ω^{2} x}{g}$
$tan θ = \frac{d y}{d x} = 10 x$
$ω = 10 r a d / sec$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity $ω$ , Two objects, each of mass m, are attached gently to the opposite ends of a diameter of the ring. The wheel now rotates with an angular velocity $ω =$
A $\frac{ω M}{M + m}$
B $\frac{ω (M - 2 m)}{M + 2 m}$
C $\frac{ω M}{M + 2 m}$
D $\frac{ω (M + 2 m)}{M}$
Question 2 - Select One
A thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity $ω$ . Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring. The ring will now rotate with an angular velocity of
A $\frac{ω (M - 2 m)}{(M + 2 m)}$
B $\frac{ω M}{(M + 2 m)}$
C $\frac{ω M}{(M + m)}$
D $\frac{ω (M + 2 m)}{M}$

RESONANCE ENGLISH-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile