To lay the cornice of a building the mason sets four bricks on top of one another in such a way that part of each brick extends beyond the brick beneath Fig.. Find the largest distances that the bricks may extend and still be in equilibrium without mortar. The length of each brick is l.
Answer: The bricks extend distances of l/2 l/4 l/6 from the top to the bottom.Explanation:Since the bricks are uniform the centre of gravity of each will be at its centre. Consequently the top brick will be in equilibrium with the brick below it if its centre of gravity lies on the line coinciding with the edge of the second brick i.e. the largest overhanging portion of the first brick is l/2.The centre of gravity of the first and second bricks taken together will be situated at a distance of 1/4 from the edge of the second brick. The second brick can extend this distance over the third.The centre of gravity of the three bricks is on line AC its position being determined from the equation Pl/2 — x = 2Px Fig. from which we obtain x = 1/6 i.e. not more than 1/6 of the third brick can extend over the fourth.
Related Solutions
Four identical bricks are kept one over another in such a way that a part of each brick is projected out of the brick below it. For equilibrium of the system, how much of the three upper bricks can be extended out?
View SolutionBrick·: Mason : : Colour : ?
View Solutionசெங்கற்களினால் கட்டப்பட்ட ஒரு படிகட்டில் மொத்தம் . 30 படிகட்டுகள் உள்ளன. கீழ்ப்படிக்கட்டை: அமைப்பதற்கு 100 செங்கற்கள் தேவைப்படுகிறது. அடுத்தடுத்த படிக்கட்டுகள் அமைப்பதற்கு முந்தைய படிக்கட்டை விட இரண்டு செங்கற்கள் குறைவாகத் தேவைப்படுகிறது. உச்சியிலுள்ள படிக்கட்டை அமைப்பதற்கு எத்தனை செங்கற்கள் தேவை?
View SolutionA mason constructs a wall of dimensions 5mx40cm xx3m with bricks each 25cm xx10cmx15cm. Calculate the total number of bricks used.
View SolutionBuilding : Brick
View Solution360 bricks are stacked in such a way that there are 30 bricks in the bottom row, 29 bricks in the next row, 28 bricks in the next row and so on. In how many rows are these 360 bricks placed and how many bricks are there in the topmost row?
View SolutionA brick staircase has a total of 30 steps. The bottom step requires 100 bricks. Each successive step requires two bricks less than the previous step.
How many bricks are required to build the stair case?View SolutionA brick staircase has a total of 30 steps. The bottom step requires 100 bricks. Each successive step requires two bricks less than the previous step. How many bricks are required to build the stair case?
View SolutionInfinite number of bricks are placed one over the other as shown in the figure. Each succeeding brick having half the length and breadth of its preceding brick and the mass of each succeeding bricks being (1//4)^(th) of the preceding one. Taking 'O' as the origin, the x coordinate of centre of mass of the system of bricks is at
View SolutionInfinite number of bricks are placed one over the other as shown in the figure. Each succeeding brick having half the length and breadth of its preceding brick and the mass of each succeeding bricks being (1//4)^(th) of the preceding one. Taking 'O' as the origin, the x coordinate of centre of mass of the system of bricks is at
View SolutionAn infinite no of bricks are placed one over the other as shown in the figure. Each succeeding brick having half the length and breadth of its precceeding brick and the mass of each succeeding bricks 1//4^(th) of the preceding one, take 'O' as the origin, the centre of mass of the system of bricks is at
View Solutionசெங்கற்களினால் கட்டப்பட்ட ஒரு படிகட்டில் மொத்தம் . 30 படிகட்டுகள் உள்ளன. கீழ்ப்படிக்கட்டை அமைப்பதற்கு 100 செங்கற்கள் தேவைப்படுகிறது. அடுத்தடுத்த படிக்கட்டுகள் அமைப்பதற்கு முந்தைய படிக்கட்டை விட இரண்டு செங்கற்கள் குறைவாகத் தேவைப்படுகிறது. படிக்கட்டுகள் முழுவதும் அமைப்பதற்கு எத்தனை செங்கற்கள் தேவை?
View SolutionA brick staircase has a total of 30 steps. The bottom step requires 100 bricks. Each successive step requires two bricks less than the previous step.
How many bricks are required for the top most step?View SolutionA brick staircase has a total of 30 steps. The bottom step requires 100 bricks. Each successive step requires two bricks less than the previous step. How many bricks are required for the top most step?
View Solutionईंट से ईंट बजाना मुहावरे का अर्थ है-
View SolutionThe volume of the brick is 2.197 L. A submerged brick is balanced by a mass 2.54 kg on a bar. The weight of brick is :
View SolutionSome bricks are arranged in an area measuring 20 cu. M. If the length, breadth and height of each brick is 25 cm 12.5 cm and 8 cm respectively, then in the pile the number of bricks are (suppose there is no gap in between two bricks)
View SolutionTo make a square courtyard which is 40 meters on each side, Rs.1080. of bricks, if the price of bricks is Rs 54 per thousand, then the area of one brick will be
View SolutionTwo identical bricks of length L are piled one on top of the other on a table as shown in the figure the maximum distance S the top brick can overhand the table with the system still balanced is:
View SolutionTwo identical bricks of length L are piled one on top of the other on a table as shown in the figure the maximum distance S the top brick can overhand the table with the system still balanced is:
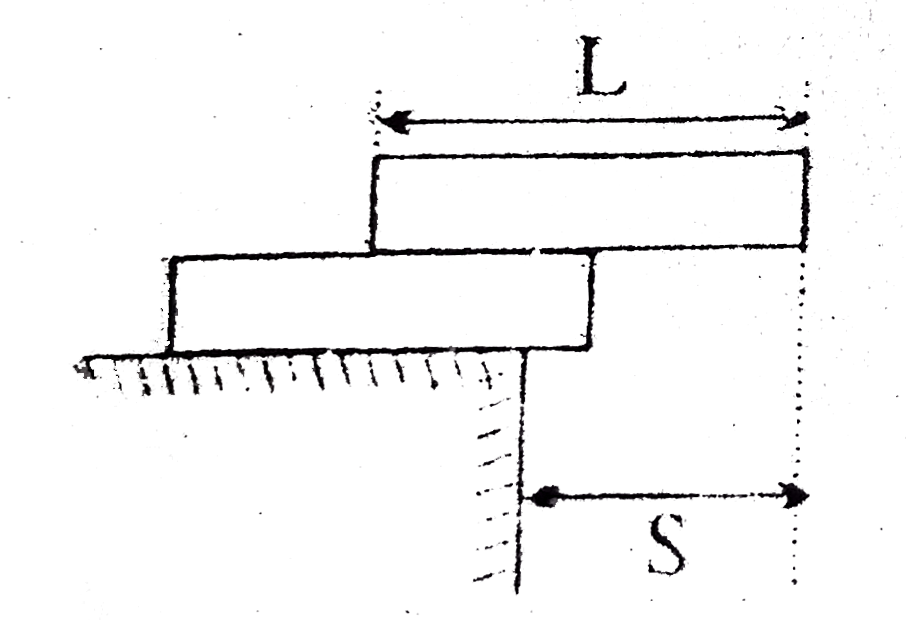 View Solution
View Solution
