For any real number x let [x] denote the largest integer less than or equal to x. Let f be a real function defined on [–10 10] byfx = {x - [x] : if [x] is odd 1 + [x] – x : if [x] is evenThen find the value of π2/10 x ∫fxcosπx dx for x ∈ [-10 10].
We have and f is periodic with period 2. Also since [–x] = 1 – [x] for non Integral values of x so f is an even function. Thus = 4
Related Solutions
For any real number x, let [x] denotes the largest integer less than or equal to x.Let f be a real valued function defined on the interval[-10,10] by
Then, the value of f(x) cos x dx is
View SolutionFor any real number , let denote the largest integer less than or equal to , Let be a real-valued function defined on the interval be is odd, is even Then the value of is____
View SolutionFor any real number , let denote the largest integer less than or equal to , Let be a real-valued function defined on the interval be is odd, is even Then the value of is____
View SolutionFor any real number , let denote the largest integer less than or equal to , Let be a real-valued function defined on the interval be is odd, is even Then the value of is____
View SolutionFor any real number x, let = largest integer less than or equalto x. Let f be a real valued function defined on the interval by
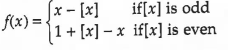 Then, the value of is
Then, the value of is
View SolutionFor any real number x, let = largest integer less than or equalto x. Let f be a real valued function defined on the interval by
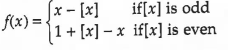 Then, the value of is
Then, the value of is
View SolutionFor any real number x, let [x] denote the largest less than or equal to x. Let f be a real valued function defined on the interval by
Show that
View SolutionFor any real number x, let [x] denote the largest integer less than or equal to x. If int_0^10 [sqrt((10x)/(x+1))]dx then the value of 9I is
View Solutionयदि एक वास्तविक x के लिए माना के महत्तम पूर्णांक मान जो x से छोटा अथवा बराबर है को दर्शाता है। मान f एक वास्तविक मान का फलन है , जो अंतराल में
द्वारा परिभाषित है
तो का मान है
View SolutionFor a real number x let [x] denote the largest number less than or equal to x. For let f (x)=[x] . Then
View SolutionFor any real number denote the largest integer less than or equal to be a real-valued function defined on the interval be Then the value of
View SolutionFor a real number x let [x] denote the largest integer less than or equal to x and Let n be a positive integer. Then is equal to
View SolutionFor a real number x let denote the largest integer less than or equal to x and . The possible integer value of n for which exceeds 2013 is
View SolutionFor a real number x let denote the largest integer less than or equal to x and . The possible integer value of n for which exceeds 2013 is
View SolutionFor real x with define , where for a real number r we denote by [r] the largest integer less than or equal to r. The number of points of discontinutiy of f in the interval (10,10) is
View SolutionFor a real number x, let [x] denote the greatest integer less than or equal to x. Let f: R R be defined as then f is
View SolutionFor a real number x let [x] denote the largest integer les than or eqaul to x and {x} =x -[x]. Let n be a positive integer. Then is equal to
View SolutionFor a real number x, let [x] denote the greatest integer less than or equal to x. Let R rarr R be defined as f(x)=2x+[x]+sin x cos x then f is
View SolutionLet n be a positive integer. For a real number x, let [x] denote the largest integer not exceeding x and {x} = . Then is equal to
View SolutionLet f be a real - valued function defined on R ( the set of real numbers) such that f(x) = sin^(-1) ( sin x) + cos^(-1) ( cos x) The value of f(10) is equal to
View Solution