For any real number x, let [x] denote the largest integer less than or equal to x, Let f be a real-valued function defined on the interval [−10,10] be f(x)={x−[x],if[x] is odd, 1+[x]−x,if[x] is even Then the value of π210∫10−10f(x)cosπxdx is____Solution in Punjabi
The correct Answer is:4
Step by step video & image solution for For any real number x, let [x] denote the largest integer less than or equal to x, Let f be a real-valued function defined on the interval [-10 , 10] be f(x)={x-[x], if [x] is odd, 1+[x]-x ,if[x] is even Then the value of (pi^2)/(10)int_(-10)^(10)f(x)cospixdx is____ by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DEFINITE INTEGRALBOOK - ARIHANT MATHSCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise For Session 1
15 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHSCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise For Session 2
14 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos
- DETERMINANTS BOOK - ARIHANT MATHSCHAPTER - DETERMINANTS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
Similar Questions
∫π/40cos2xdx
View SolutionEvaluate ∫π/40log(1+tanθ)dθ
View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
View SolutionIf a2+b2+c2=−2, and f(x)= ∣∣ ∣ ∣∣1+a2x(1+b2)x(1+c2)x(1+a2)x1+b2x(1+c2)x(1+a2)x(1+b2)x1+c2x∣∣ ∣ ∣∣ , then f(x) is a polynomial of degree
View SolutionFor any real number x,let[x] denote the largest integer less than or equal to x,Letf be a real-valued function defined on the interval [−10,10] be f(x)={x−[x],if[x]isodd1+[x]−x,if[x]iseven Then the value of π210∫10−1f(x)cosπxdxis__
View SolutionLet f(x)=sqrt(log_(10)x^(2)) then the set of all values of x for which f(x) is real is
View SolutionFor a real number x, let [x] denote the greatest integer less than or equal to x. Let R rarr R be defined as f(x)=2x+[x]+sin x cos x then f is
View SolutionFor a real number x let [x] denote the largest number less than or equal to x. For x∈R let f (x)=[x] sinπx. Then
View Solutionf(x)={x−[x],if[x]is odd1+[x]−x,if[x] is even
Then, the value of π210∫10−10f(x)cosπ×dx is
View SolutionLet f be a real - valued function defined on R ( the set of real numbers) such that f(x)=sin−1(sinx)+cos−1(cosx)
The value of f(10) is equal to
View SolutionLet f:R→R is a function defined as f(x) where ={|x−[x]|:[x]is odd|x−[x+1]|:[x]is even
[.] denotes the greatest integer function, then ∫4−2dx is equal to
View Solutionदिया है कि किसी वास्तविक संख्या x के लिए [x], अधिकतम पूर्णांक को दर्शाता है यदि अन्तराल [−10,10] पर वास्तविक मानों वाला फलन f निम्न प्रकार से परिभाषित है f(x)={x−[x],if [x] is Odd,1+[x]−x, if [x] is Even तो π210∫10−10f(x)cosπxdx का मान है
View SolutionGiven that [x] of a real number x, the maximum integer le x It reflects. If the function f with real values at the interval [-10, 10] is defined as follows f(x)={{:(x-[x],"यदि [x] विषम है"),(1+[x]-x,"यदि [x] सम है"):} so (pi^2)/(10)int_(-10)^(10)f(x)cos pi xx dx The value of
View SolutionFor any real number x, let [x]= largest integer less than or equalto x. Let f be a real valued function defined on the interval[−10,10] by
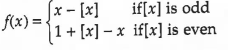 Then, the value of (π10)2(∫10−10f(x)cosπxdx is
Then, the value of (π10)2(∫10−10f(x)cosπxdx is
View SolutionFor any real number x, let [x] denote the largest less than or equal to x. Let f be a real valued function defined on the interval [−10,10] by f(x)={x−[x],if [x] is odd1+[x]−x,if [x] is even
Show that ∫10−10f(x)cosπdx=4
View Solutionयदि एक वास्तविक x के लिए माना [x],x के महत्तम पूर्णांक मान जो x से छोटा अथवा बराबर है को दर्शाता है। मान f एक वास्तविक मान का फलन है , जो अंतराल [−10,10] में
f(x)={x−[x]1+[x]−x
f(x)={x−[x] यदि [x] विषम 1+[x]−x यदि [x]सम द्वारा परिभाषित है
तो p21010∫−10f(x)cosπxdx का मान है
View Solution
