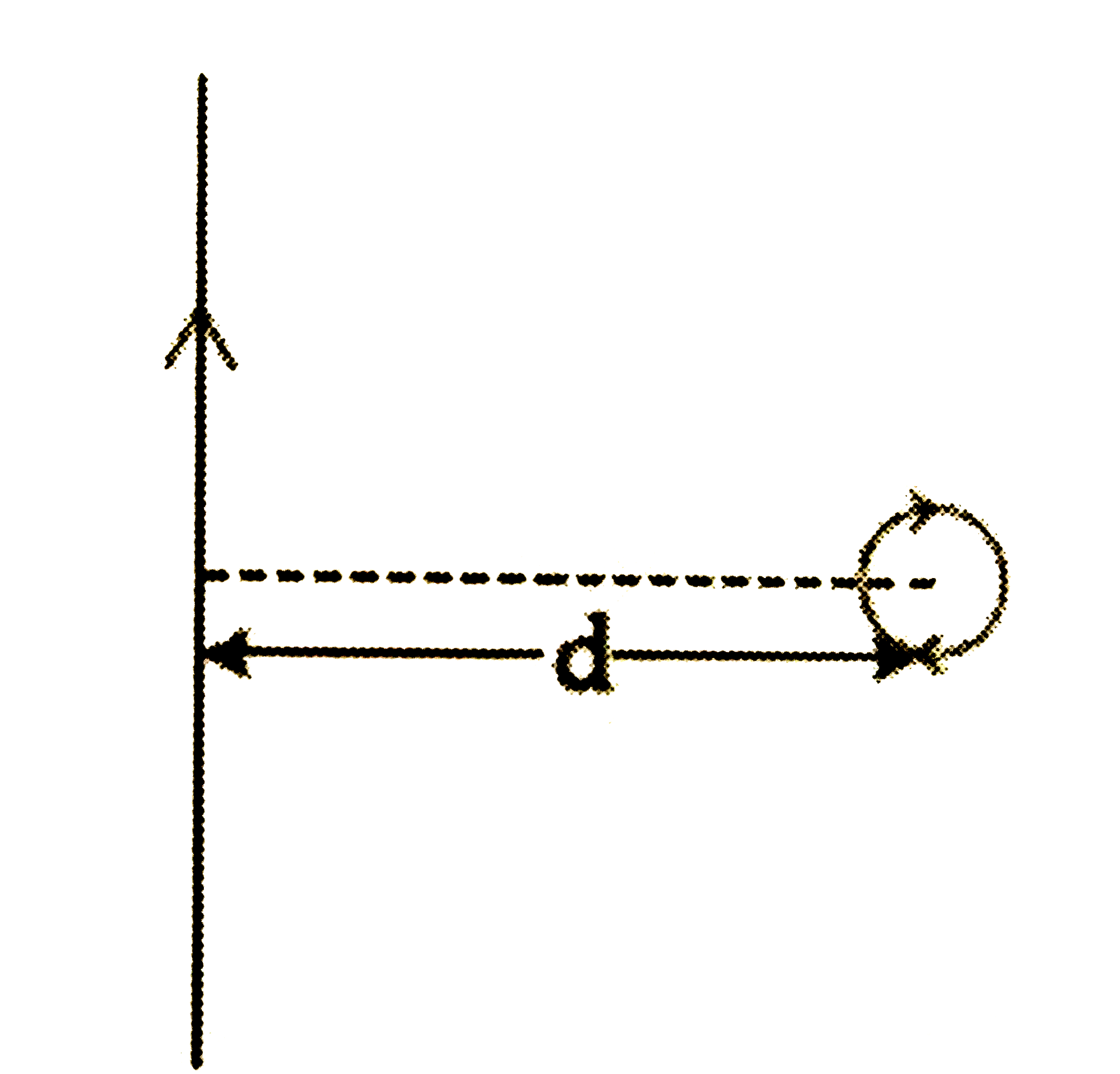
Two infinitely long straight wires lie in the xy-plane along the lines x = ±R. The wire located at x = +R carries a constant current I1 and the wire located at x = –R carries a constant current I2. A circular loop of radius R is suspended with its centre at 0 0 √3R and in a plane parallel to the xy-plane. This loop carries a constant current I in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the +j direction. Which of the following statements regarding the magnetic field vector B is are true ? A If I1 = I2 then vector B cannot be equal to zero at the origin 0 0 0 B If I1 > 0 and I2 0 then vector B can be equal to zero at the origin 0 0 0 D If I1 = I2 then the z-component of the magnetic field at the centre of the loop is -μ0I/2R
Related Solutions
Two infinitely long straight wires lie in the xy-plane along the lines . The wire located at carries a constant current and the wire located at carries a constant current . A circular loop of radius R is suspended with its centre at and in a plane parallel to the xy-plane. This loop carries a constant current ? in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the direction. Which of the following statements regarding the magnetic field is (are) true?
View SolutionTwo infinitely long straight wires lie in the xy-plane along the lines . The wire located at carries a constant current and the wire located at carries a constant current . A circular loop of radius R is suspended with its centre at and in a plane parallel to the xy-plane. This loop carries a constant current ? in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the direction. Which of the following statements regarding the magnetic field is (are) true?
View SolutionTwo straight length xy straight wires in xy-plane x = +- R Are placed on the lines. x = + R On the wire I_(1) And x = - R On the wire I_(2) Steady currents are flowing. R A circular loop of radius, the center of which (0, 0, sqrt(3)R) Is, thus, hanging such that the plane of the loop is parallel to the xy-plane. A constant curent is flowing in the loop. When viewed from above the loop, the direction of the current in the loop is clockwise. The current in a wire of infinite length is considered positive if it is a unit vector. +hatj Is in the direction of. Magnetic field vec(B) Which of the following statements (s) is (are) correct about
View SolutionA circuit consists of a circular loop of radius R kept in the plane of paper and an infinitely long current carrying wire kept perpendicular to the plane of paper and passing through the centre of loop. The mutual inductance of wire and loop will be
View SolutionA circuit consists of a circular loop of radius R kept in the plane of paper and an infinitely long current carrying wire kept perpendicular to the plane of paper and passing through the centre of loop. The mutual inductance of wire and loop will be
View SolutionA circular loop of radius R, carrying current I, lies n XY-plane with its centre at origin. The total magnetic flux through XY-plane is
View SolutionAn infinitely long current carrying wire and a small current carrying loop are in the plane of the paper as shown. The radius of the loop is a and distance of its centre from the wire is d (d>>a). If the loop applies a force F on the wire then :
 View Solution
View SolutionA circular loop of radius carries a current .How should a long, straight wire carrying a current be placed in the plane of the circle so that the magnetic field at the centre of the loop becomes zero?
View SolutionIn the figure, a long straight wire carrying a current and a loop of a square conducting wire of side l are located at a distance 'a' from the current carrying wire, both the current carrying wire and the loop are in the plane of the paper, find the magnetic flux of the current carrying wire passing through the loop Do it
View SolutionA long straight wire is carrying current in direction. The x-y plane contains a closed circular loop carrying current and not encircling the straight wire, then the force (in newton) on the loop will be ? (radius of the circular loop ).
View SolutionA circular loop of radius r carries a current i. How should a long , straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
View SolutionA circular loop of radius r carries a current i. where should a long , straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
View SolutionA circular loop of radius r carries a current i. where should a long , straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
View SolutionThere is a circular loop carrying current and another straight wire carrying current is placed along its axis. The straight wire
View SolutionA rectangular loop carrying a current i_(2) situated near a long straight wire carrying a steady current i_(1) . The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
View SolutionA rectangular loop carrying a current i_(2) situated near a long straight wire carrying a steady current i_(1) . The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
View SolutionA circular loop of radius R in X-Y plane with its centre at origin is carrying current I. The total magnetic flux through X-Y plane is
View SolutionA circular loop of radius R in X-Y plane with its centre at origin is carrying current I. The total magnetic flux through X-Y plane is
View Solutionत्रिज्या r का एक वृताकार लूप जिसमे I धारा प्रवाहित हो रही है X-Y तल में स्थित है जिसका केंद्र मूल बिंदु पर है X-Y तल से गुजरने वाला कुल चुंबकीय फ्लेक्स क्या होगा
View Solutionचित्र में दर्शाए अनुसार R त्रिज्या का एक वृत्ताकार तार लूप (पाश) x-y तल में\ रखा है और इसका केन्द्र 0 पर है। इस वृत्ताकार लूप के अक्ष पर भुजा a (a< R पर है (चित्र देखिए)। कुण्डली का तल :-अक्ष से कोण पर है। यदि लूप और कुण्डली का अन्योन्य प्रेरकत्व है, तब p का मान क्या है?
 View Solution
View Solution
