A circular loop of radius r carries a current i. where should a long , straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
To solve the problem of where to place a long straight wire carrying a current of 4i in the plane of a circular loop of radius r carryingacurrenti such that the magnetic field at the center of the loop becomes zero, we can follow these steps:
1. Understand the Magnetic Fields:
- The magnetic field at the center of a circular loop carrying current i is given by the formula:
Bloop=μ0I2r
- For a long straight wire carrying current 4i, the magnetic field at a distance D from the wire is given by:
Bwire=μ0(4i)2πD
2. Set Up the Equation for Zero Magnetic Field:
- For the magnetic field at the center of the loop to be zero, the magnetic field due to the loop must equal the magnetic field due to the wire, but in opposite directions:
Bloop=Bwire
- This leads to the equation:
μ0I2r=μ0(4i)2πD
3. Cancel Common Terms:
- We can cancel μ0 from both sides and 2 as well:
Ir=4iπD
4. Rearranging the Equation:
- Rearranging the equation gives:
πD=4r
- Therefore, we can solve for D:
D=4rπ
5. Conclusion:
- The distance D from the center of the loop to the long straight wire where the magnetic field at the center becomes zero is:
D=4rπ
Final Answer:
The long straight wire should be placed at a distance D=4rπ from the center of the circular loop.
- The magnetic field at the center of a circular loop carrying current i is given by the formula:
Bloop=μ0I2r
- For a long straight wire carrying current 4i, the magnetic field at a distance D from the wire is given by:
Bwire=μ0(4i)2πD
- For the magnetic field at the center of the loop to be zero, the magnetic field due to the loop must equal the magnetic field due to the wire, but in opposite directions:
Bloop=Bwire
- This leads to the equation:
μ0I2r=μ0(4i)2πD
- We can cancel μ0 from both sides and 2 as well:
Ir=4iπD
- Rearranging the equation gives:
πD=4r
- Therefore, we can solve for D:
D=4rπ
- The distance D from the center of the loop to the long straight wire where the magnetic field at the center becomes zero is:
D=4rπ
The long straight wire should be placed at a distance D=4rπ from the center of the circular loop.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer12videos
MAGNETIC FIELD DUE TO CURRENT
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 27videos
MAGNETIC FIELD DUE TO CURRENT
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer6videos
MAGNETIC PROPERTIES OF MATTER
Similar Questions
A circular loop of radius r carries a current i. How should a long, straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the center becomes zero?
View SolutionA wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
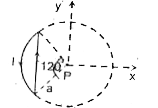 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
 View Solution
View SolutionA conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.
 View Solution
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View Solution
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius RView SolutionA circular loop of radius R carries a current I. Another circular loop of radius r(ltltR) carries a current I. The plane of the smaller loop makes an angle of 90^@ with that of the larger loop. The planes of the two circles are at right angle to each other. Find the torque acting on the smaller loop.
View SolutionA square conducting loop is placed in the neighbourhood of a coplaner long straight wire carrying a current i.
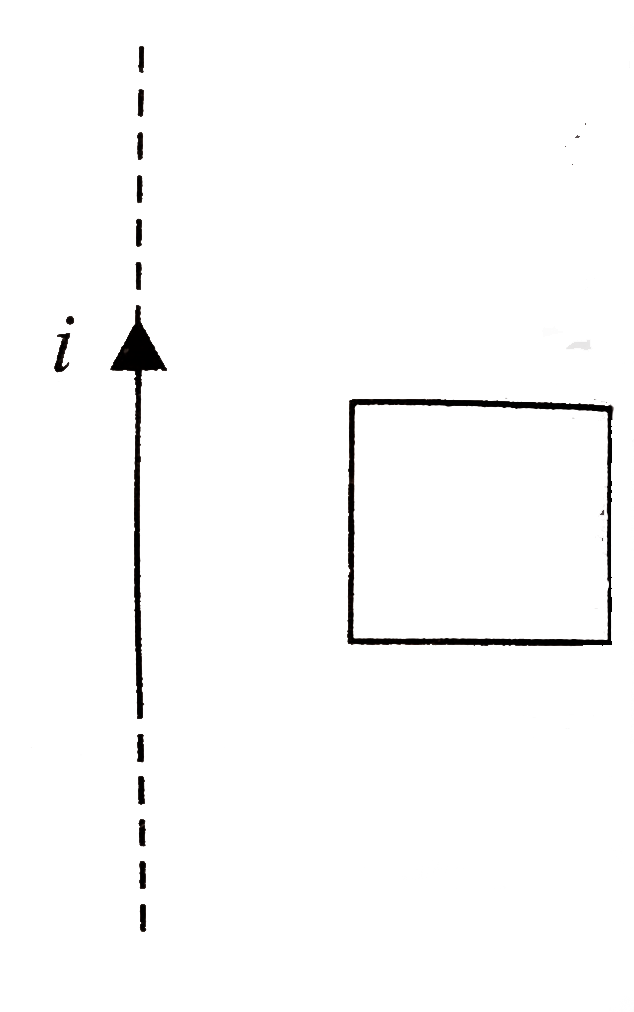 View Solution
View SolutionA circular coil of radius R carries a current i. The magnetic field at its centre is B. The distance from the centre on the axis of the coil where the magnetic field will be B/8 is
View Solution

