Two infinitely long straight wires lie in the xy-plane along the lines x=±R. The wire located at x=+R carries a constant current I1 and the wire located at x=−R carries a constant current I2. A circular loop of radius R is suspended with its centre at (0,0,√3R) and in a plane parallel to the xy-plane. This loop carries a constant current ? in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the +ˆJ direction. Which of the following statements regarding the magnetic field →B is (are) true?
If I1=I2, then →Bcannot be equal to zero at the origin (0, 0, 0)
If I1>0 and I2<0, then →B can be equal to zero at the origin (0, 0, 0)
If I1<0 and I2>0 then →Bcan be equal to zero at the origin (0, 0, 0)
If I1=I2, then the z-component of the magnetic field at the centre of the loop is (−μ0I2R)
The correct Answer is:A, B, D
To solve the problem regarding the magnetic field generated by two infinitely long straight wires and a circular loop, we will follow these steps:
Step 1: Understand the Configuration
We have two infinitely long straight wires located at x=+R and x=−R in the xy-plane. The wire at x=+R carries a current I1 in the positive y-direction, and the wire at x=−R carries a current I2 in the negative y-direction. A circular loop of radius R is centered at (0,0,√3R) and carries a current I in the clockwise direction as viewed from above.
Step 2: Determine the Magnetic Field Due to Each Wire
Using the formula for the magnetic field around a long straight wire:
B=μ0I2πr
where r is the distance from the wire.
- For wire 1 at x=+R:
- The distance from the center of the loop to wire 1 is √R2+(√3R)2=√4R2=2R.
- The magnetic field B1 due to wire 1 at the center of the loop is:
B1=μ0I12π(2R)=μ0I14πR
- The direction of B1 is determined using the right-hand rule and points in the positive z-direction (out of the page).
- For wire 2 at x=−R:
- The distance from the center of the loop to wire 2 is also 2R.
- The magnetic field B2 due to wire 2 at the center of the loop is:
B2=μ0I22π(2R)=μ0I24πR
- The direction of B2 points in the negative z-direction (into the page).
Step 3: Calculate the Net Magnetic Field Due to the Wires
- If I1=I2, then:
Bnet=B1−B2=μ0I14πR−μ0I24πR=0
Thus, the magnetic field due to the wires cancels out at the center of the loop.
Step 4: Determine the Magnetic Field Due to the Loop
The magnetic field at the center of the loop due to the loop itself is given by:
Bloop=μ0I2R
Since the current in the loop is clockwise, the direction of Bloop is in the negative z-direction (into the page).
Step 5: Combine the Magnetic Fields
- If I1=I2, the total magnetic field at the center of the loop is:
Btotal=Bloop+Bnet=−μ0I2R+0=−μ0I2R
Conclusion
The magnetic field at the center of the loop is non-zero and directed into the page when I1=I2.
We have two infinitely long straight wires located at x=+R and x=−R in the xy-plane. The wire at x=+R carries a current I1 in the positive y-direction, and the wire at x=−R carries a current I2 in the negative y-direction. A circular loop of radius R is centered at (0,0,√3R) and carries a current I in the clockwise direction as viewed from above.
Using the formula for the magnetic field around a long straight wire:
B=μ0I2πr
where r is the distance from the wire.
- The distance from the center of the loop to wire 1 is √R2+(√3R)2=√4R2=2R.
- The magnetic field B1 due to wire 1 at the center of the loop is:
B1=μ0I12π(2R)=μ0I14πR
- The direction of B1 is determined using the right-hand rule and points in the positive z-direction (out of the page).
- The distance from the center of the loop to wire 2 is also 2R.
- The magnetic field B2 due to wire 2 at the center of the loop is:
B2=μ0I22π(2R)=μ0I24πR
- The direction of B2 points in the negative z-direction (into the page).
- If I1=I2, then:
Bnet=B1−B2=μ0I14πR−μ0I24πR=0
Thus, the magnetic field due to the wires cancels out at the center of the loop.
The magnetic field at the center of the loop due to the loop itself is given by:
Bloop=μ0I2R
Since the current in the loop is clockwise, the direction of Bloop is in the negative z-direction (into the page).
- If I1=I2, the total magnetic field at the center of the loop is:
Btotal=Bloop+Bnet=−μ0I2R+0=−μ0I2R
The magnetic field at the center of the loop is non-zero and directed into the page when I1=I2.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Main (Archive)75videos
MAGNETIC EFFECTS OF CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)55videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)10videos
MOCK TEST 1
Similar Questions
What will be magnetic field at centre of current carrying circular loop of radius R?
View SolutionA circular loop of radius R carries current I2 in a clockwise direction as shown in figure. The centre of the loop is a distance D above a long, straight wire. What are the magnitude and direction of the current I1 in the wire if the magnetic field at the centre of loop is zero?
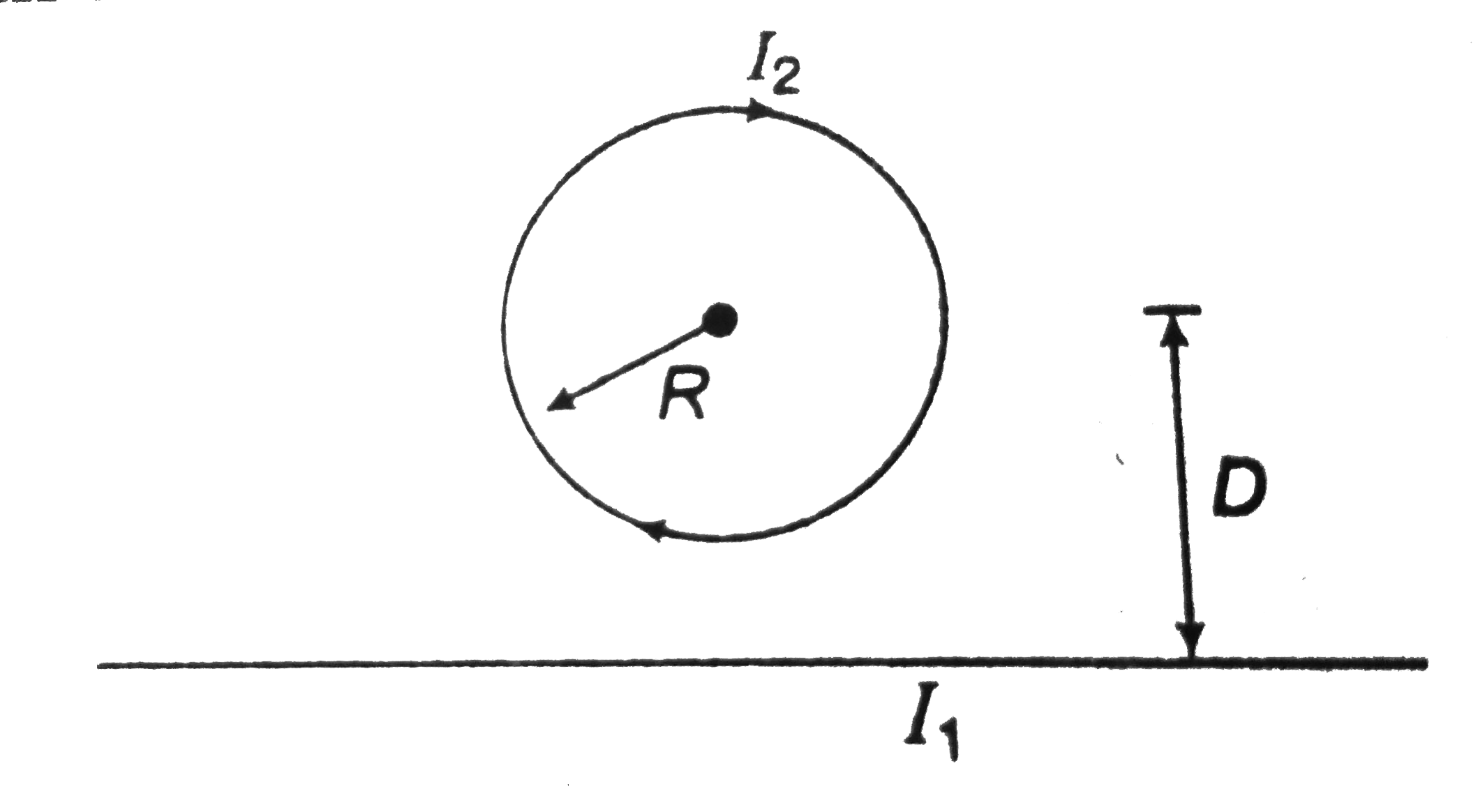 View Solution
View SolutionA circular loop of wire of radius R is bent about its diameter along two mutually perpendicular planes as shown in Fig. If the loop carries a current I, then determine its magnetic moment.
View SolutionA circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
View SolutionA circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
View SolutionA current − carrying circular loop of radius R is placed in the XY− plane with centre at the origin. Half of the loop with x>0 is now bent so that is now lies in the YZ− plane
View SolutionTwo infinitely long, thin, insulated, straight wires lie in the x-y plane along the x- and y- axis respectively. Each wire carries a current I, respectively in the positive x-direction and positive y-direction. The magnetic field will be zero at all points on the straight line:
View SolutionA circular loop of radius r carries a current i. where should a long , straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
View SolutionEach of two long parallel wires carries a constant current i along the same direction . The wires are separated by a distance 2I. The magnitude of resultant magnetic induction in the symmetric plane of this system located between the wires at a distance R from each wire will be
View SolutionA long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
View Solution

