In the figure the side QR of ∆PQR is produced to a point S. If the bisectors of ∠ PQR and ∠ PRS meet at point T then prove that ∠QTR = 1/ 2 ∠QPR.
Exterior ∠PRS = ∠PQR + ∠QPR [Exterior angle property] Therefore 1 2 ∠PRS = 1 2 ∠PQR + 1 2 ∠QPR ⇒ ∠TRS = ∠TQR + 1 2 ∠QPR …i But in ∆QTR Exterior ∠TRS = ∠TQR + ∠QTR …ii [Exterior angles property] Therefore from i and ii ∠TQR + ∠QTR = ∠TQR + 1 2 ∠QPR ⇒ ∠QTR = 1 2 ∠QPR Proved.
Related Solutions
In Fig. 6.44, the side QR of is produced to a point S. If the bisectors of and meet at point T, then prove that .
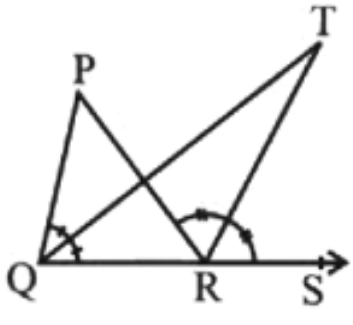
View SolutionIn figure, the side of is produced to a point S. If the bisectors. of meet at point T, then prove that .
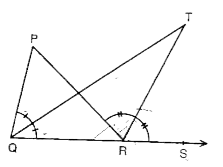
View SolutionIn Fig , the side QR and is produced to a point S. If the bisector of meet at point T the prove that
View SolutionIn Figure, is a point on side of and is a point such that Prove That :
View SolutionIn Fig. , the side QR of △ PQR is produced to a point S. If the bisectors of and meet at point T, then prove that .

View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of and meet at point T, then prove that .

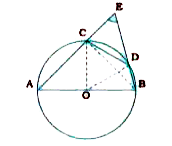
View SolutionIn the given figure, AB is a diameter of the circle, CD is chord equal to the radius of the circle, AC and BD when extended intersect at a point E. Prove that
View SolutionIn an isosceles triangle PQR, PQ =PR and S is any point on side QR. Then prove that:
View SolutionIn an isosceles triangle PQR, PQ =PR and S is any point on side QR. Then prove that:
View SolutionTriangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that :
View Solutionमें, PQ = PR भुजा PR एक बिंदु x इस प्रकार है कि सिद्ध कीजिए कि
View SolutionIn the adjoining figure, angle PQR = 90^(@)T is the midpoint of side QR. Prove that PR^(2) = 4PT^(2) - 3PQ^(2)
View SolutionPQR is a triangle, whose are is . S is a point on side QR, such that PS is the angle bisector of . If PQ : PR = 2 : 3 , then what is the area (in ) triangle PSR ?
View SolutionIn Fig. 6.1, side QR of a has been produced to the point S. If and,then ∠Q is equal to,
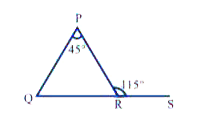
View SolutionIn and PO is the bisector of . If and then in degrees
View SolutionS and T are point on sides and of such that . Show that .
View SolutionS and T are points on sides PR and QR of such that . Show that .
View Solutionकी भुजाएँ PR और QR पर S और T बिन्दुएँ इस प्रकार है , कि दिखाये कि
View SolutionS and T are points on sides PR and QR of Delta PQR such that /_P=/_RTS show that Delta RPQ-Delta RTS
View SolutionS and T are points on sides PR and QR of such that Show that
View Solution