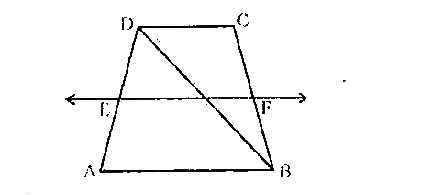
ABCD is a trapezium in which AB || DC BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F see Fig.. Show that F is the mid-point of BC
Given : A trapezium ABCD with AB || DC E is the mid-point of AD and EF || AB. To Prove : F is the mid-point of BC. Proof : AB || DC and EF || AB ⇒ AB EF and DC are parallel. Intercepts made by parallel lines AB EF and DC on transversal AD are equal. ∴ Intercepts made by those parallel lines on transversal BC are also equal. i.e. BF = FC ⇒ F is the mid-point of BC.
Related Solutions
ABCD is a trapezium in which , BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F. Show that F is the mid-point of BC.
View SolutionABCD is a trapezium in which BD is a diagonal and E is the mid point of AD. A line is drawn through E parallel to AB intersecting BC at F. Show that F is the mid point of BC.
View SolutionABCD is a trapezium, in which AB||DC are a diagonal and E is the mid point of AD. A is drawn through E, parallel to AB intersect BC at F. Show that F is the mid point of BC
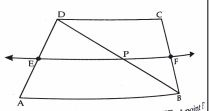
View SolutionABCD is a trapezium, in which AB||DC are a diagonal and E is the mid point of AD. A is drawn through E, parallel to AB intersect BC at F. Show that F is the mid point of BC
View SolutionE is the mid-point of the side AD of the trapezium ABCD with . A line through E drawn parallel to AB intersects BC at F. then
View SolutionE is the mid-point of the side AD of the tarapezium ABCD with . A line through E drawn parallel to AB intersects BC at F. Show that F is the mid-points of BC.
View SolutionABCD is a trapezium in which , BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
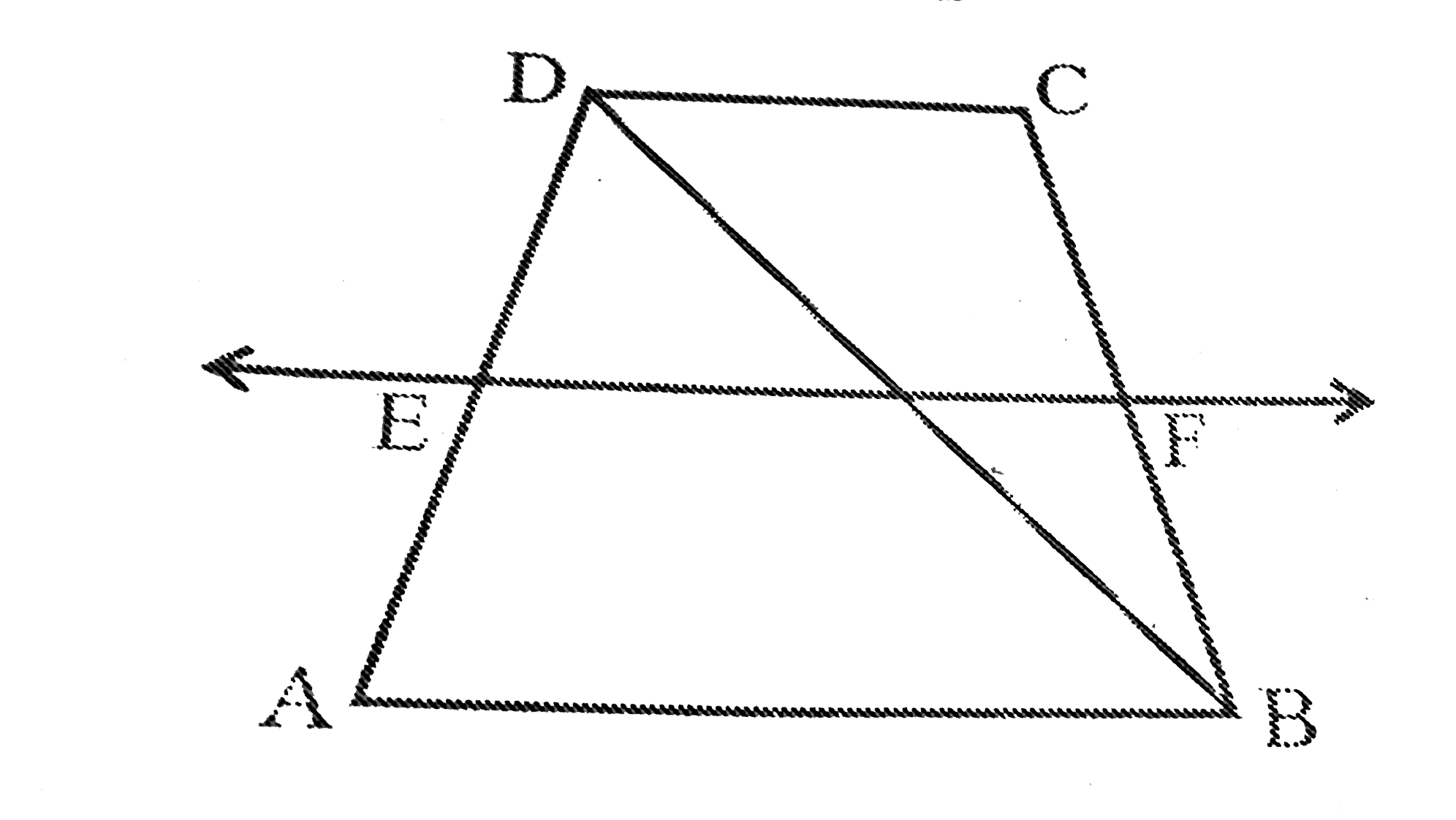
View SolutionABCD is a trapezium in which , BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.

View Solutionएक समलम्ब है जिसमें है । साथ ही BD एक विकर्ण है और E भुजा AD का मध्य बिंदु है । E से होकर एक रेखा AB के समांतर खींची गई है जो BC को पर प्रतिच्छेद करती है। दर्शाइए कि भुजा BC का मध्य बिंदु है।

View SolutionIn a trapezium ABCD, AB/DC, E is mid-point of aD. A line through E and parallel to AB intersects BC at point F. Show that:
2EF=AB+DC
View SolutionIn trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that : AB + DC = 2EF.
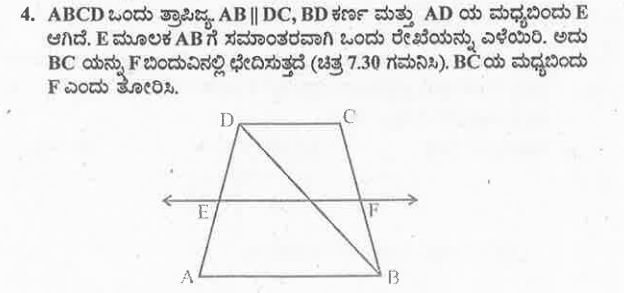
View SolutionABCD ಒಂದು ತ್ರಾಪಿಜ್ಯ AB DC, BD ಕರ್ಣ ಮತ್ತು AD ಯ ಮಧ್ಯಬಿಂದು E ಆಗಿದೆ. E ಮೂಲಕ AB ಗೆ ಸಮಾಂತರವಾಗಿ ಒಂದು ರೇಖೆಯನ್ನು ಎಳೆಯಿರಿ. ಅದು BC ಯನ್ನು F ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುತ್ತದೆ (ಚಿತ್ರ 7ಗಮನಿಸಿ) BC ಯ ಮಧ್ಯಬಿಂದು F ಎಂದು ತೋರಿಸಿ.
View SolutionABCD is a trapezium in which AB || DC and E is the mid-point of AD. If F be a point on BC such that EF || DC, then prove that
View SolutionABCD is a trapezium with AB || DC. E is midpoint of side AD. From point E a line is drawn parallel to AB that intersects BC at F. Show that F is midpoint of BC.
View SolutionABCD is a trapezium in which AB||DC and let E be the mid point of AD. Let F be a point on BC such that EF||AB. Prove that F is mid point of BC.
View SolutionLet ABCD be a trapezium in which AB||DC and E be the mid-point of AD. If F be a point on BC such that EF||AB. Then EF, where F is the mid-point of BC, is equal to
View SolutionAB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
View SolutionAB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
View SolutionABCD एक समलंब है, जिसमें है। साथ , BD एक विकर्ण है और भुजा का मध्य -बिंदु है। से होकर एक रेखा के समांतर खींची गई है को पर प्रतिच्छेद करती है। दर्शाइए कि भुजा का मध्य - बिंदु है।

View SolutionIn trapezium , and are parallel. A straight line parallel to intersects and at the points and respectively. Prove that .
View Solution