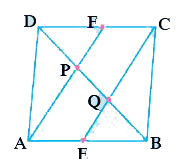
In a parallelogram ABCD E and F are the mid-points of sides AB and CD respectively see Fig.. Show that the line segments AF and EC trisect the diagonal BD.
Given : A parallelogram ABCD in which E and F are mid-points of sides AB and DC respectively. To Prove : DP = PQ = QB Proof : Since E and F are mid-points of AB and DC respectively. ⇒ AE = 1/ 2 AB and CF = 1 /2 DC …i But AB = DC and AB || DC …ii [Opposite sides of a parallelogram] ∴ AE = CF and AE || CF. ⇒ AECF is a parallelogram. [One pair of opposite sides is parallel and equal] In ∆BAP E is the mid-point of AB EQ || AP ⇒ Q is mid-point of PB [Converse of mid-point theorem] ⇒ PQ = QB …iii Similarly in ∆DQC P is the mid-point of DQ DP = PQ …iv From iii and iv we have DP = PQ = QB or line segments AF and EC trisect the diagonal BD. Proved.
Related Solutions
In a parallelogram ABCD, E and F are the mid points of sides AB and CD respectively (see fig.) Show that the line segements AF and EC trisect the diagonal BD.
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.

View SolutionIn a parallelogram ABCD, E and F are the mid points of sides AB and CD respectively show that the line segments AF and EC trisect the diagonal BD

View SolutionIn a parallelogram ABCD, E and F are the mid points of sides AB and CD respectively show that the line segments AF and EC trisect the diagonal BD

View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.

View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.

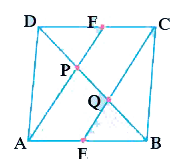
View SolutionIn a parallelogram ABCD, E and F are the midpoints of the sides AB and DC respectively. Show that the line segments AF and EC trisect the diagonal BD.
View SolutionIn a parallelogram ABCD, E and F are the midpoints of the sides AB and DC respectively. Show that the line segments AF and EC trisect the diagonal BD.
View SolutionIn a parallelogram ABCD, E and F are the midpoints of the sides AB and DC respectively. Show that the line segments AF and EC trisect the diagonal BD.

View SolutionIn a parallelogram ABCD, points E and F are respectively midpoint of sides AB and CD (see the adjacent figure). Prove that line segment AF and EC trisect diagonal BD.
View SolutionIn the fig ABCD is a parallelogram in which E and F are mid points of AB and CD respectively. Prove that the line segments CE and AF intersect diagonal BD
View SolutionE and F are the mid-points of the sides AB and CD of a parallelogram ABCD. Prove that the line segment AF and CE trisects BD in three equal parts.
View SolutionShow that the points between AB and DC in the parallelogram ABCD, the lines AF and EC E and F, respectively, triple the diagonal BD.
View SolutionIn parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The lines segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that :
GEHF is a parallelogram.
View SolutionIn parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The lines segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that :
triangle HEB and FHC are congruent.
View SolutionIf the mid points of the sides AB and AC of a triangle ABC are a n d then the length of the side BC in cm is
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View Solutionਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਵਿਚ E ਅਤੇ F ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ AB ਅਤੇ CD ਦੇ ਮੱਧ-ਬਿੰਦੂ ਹਨ (ਦੇਖੋ ਚਿੱਤਰ 8.31)। ਦਰਸਾਉ ਕਿ ਰੇਖਾ ਖੰਡ AF ਅਤੇ EC ਵਿਕਰਣ BD ਨੂੰ ਤਿੰਨ ਬਰਾਬਰ ਭਾਗਾਂ ਵਿਚ ਵੰਡਦਾ ਹੈ।

View SolutionABCD is a parallelogram. E and F are mid-point of side AB and CD respectively. AF and CE intersect diagonal BD at P & Q respectively. If BD = 15 cm, find PQ.

View Solution