A uniform solid disk is set into rotation with an angular speed about an axis through its center. While still rotating at this speed the disk is placed into contact with a horizontal surface and released as shown in Figure 11.64. a What is the angular speed of the disk once pure rolling takes place? b Find the fractional loss in kinetic energy from the time the disk is released until the time pure rolling occurs. Hint: Consider torque about the center of mass.
This is the solution hereClick here to view
Related Solutions
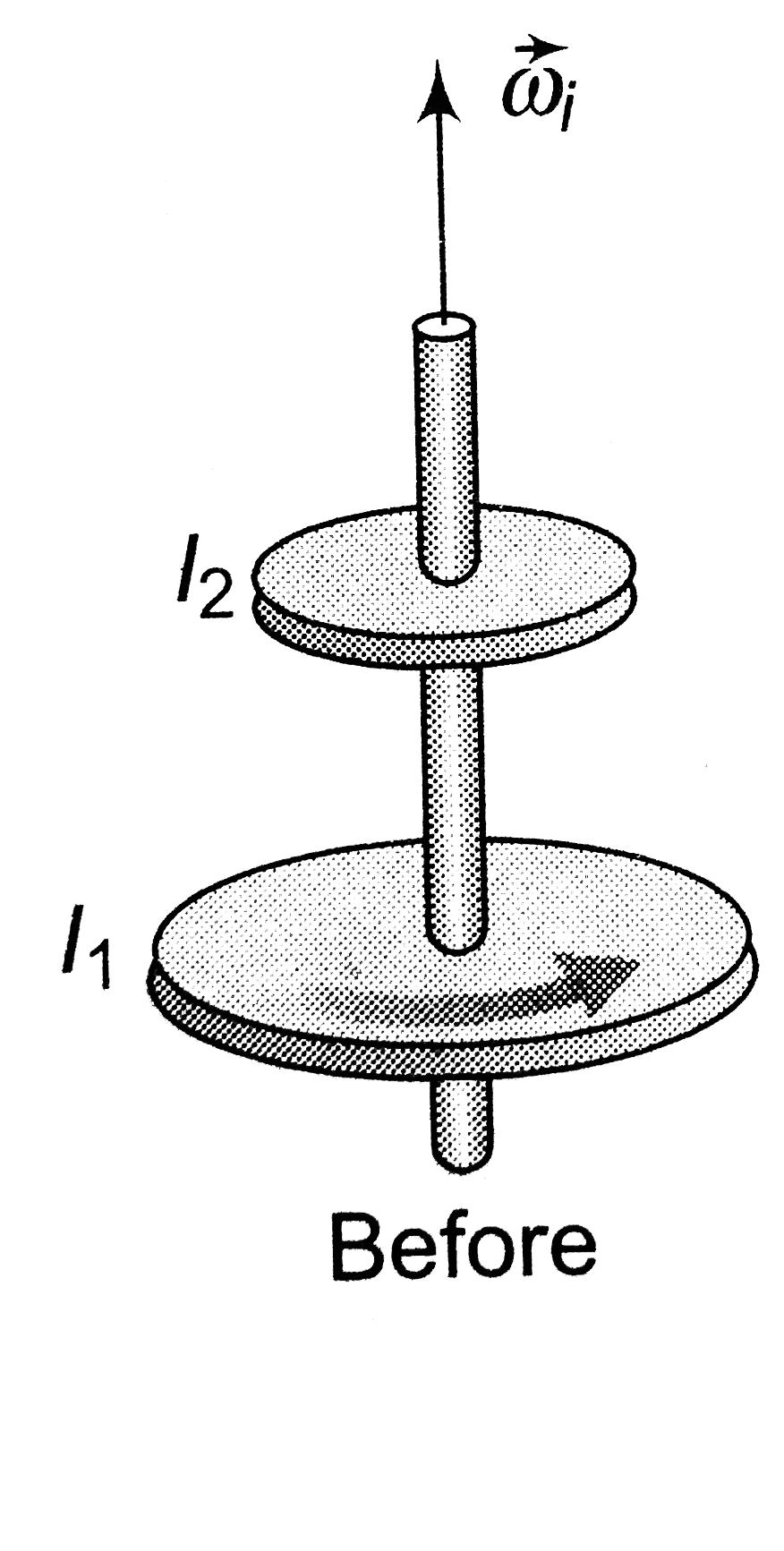
A circular disk of moment of inertia is rotating in a horizontal plane , about its symmetry axis , with a constant angular speed . Another disk of moment of inertia is dropped coaxially onto the rotating disk . Initially the second disk has zero angular speed . eventually both the disks rotate with a constant angular speed . The energy lost by the initially rotating disc to friction is
View SolutionA unifrom solid disk of radius and mass is free to rotate on a frictionless pivot through a point on its rim. If the disk is released from rest in the position shown in figure. The speed of the lowest point on the disk in the dashed position is.
 .View Solution
.View SolutionA thin circular disk of radius R is uniformly charged with density per unit area. The disk rotates about its axis with a uniform angular speed . The magnetic moment of the disk Is
View SolutionA thin circular disk of radius is uniformly charged with density per unit area.The disk rotates about its axis with a uniform angular speed .The magnetic moment of the disk is :
View SolutionA thin circular disk of radius is uniformly charged with density per unit area.The disk rotates about its axis with a uniform angular speed .The magnetic moment of the disk is :
View SolutionA circular disk of moment of inertia I_t is rotating in a horizontal plane, about its symmetry axis,with a constant angular, speed omega_1 Another disk of moment of inertia I_b is dropped coaxially onto the rotating disk initially the second disk has zero angular speed.Eventually both the disks rotate with a constant angular speed omega_f The energy lost by the initially rotating disc to friction is :
View SolutionTwo identical disks A and B can spin around vertical axes. Disk A is spinning with an initial angular speed of 40 rev/s when its rim touches initially stationary disk B, causing that disk to begin to spin. The rubbing at the contact point slows A while speeding up B. The rate at which both disks change their angular speeds is 2.0rev//s^(2) . Find the time required for the two disks to reach the same angular speed.
View SolutionA flat uniform circular disk (radius = 2.00 m, kg) is initially stationary. The disk is free to rotate in the horizontal plane about a frictionless axis perpendic ular to the center of the disk. A 40.0-kg person, standing 1.25 m from the axis, begins to run on the disk in a circular path and has a tangential speed of relative to the ground. Find the resulting angular speed of the disk (in ) and describe the direction of the rotation.
View Solutionजड़त्व आघूर्ण की एक वृत्ताकार डिस्क अपनी सममिति अक्ष के परितः, एक स्थिर कोणीय वेग से क्षैतिज तल में घूर्णन कर रही है। इस डिस्क के ऊपर जड़त्व आघूर्ण की एक अन्य डिस्क संकेन्द्री डाल दी जाती है। प्रारंभ में दूसरी डिस्क की कोणीय चाल शून्य है। अन्ततः दोनों डिस्क एक ही स्थिर कोणीय वेग से घूर्णन करने लगती हैं। प्रारंभ में घूर्णन करती हुई डिस्क की घर्षण के कारण नष्ट हुई ऊर्जा है ।
View Solutionत्रिज्या R की एक अचालकीय चकती के पृष्ठ पर आवेश Q को एक समान रूप से वितरित किया गया है। चकती कोणीय वेग से अपने केन्द्र से गुजर रही और तल के लम्बवत् अक्ष पर घूर्णन कर रही है। इस घूर्णन के फलस्वरूप चकती के केन्द्र पर चुम्बकीय क्षेत्र का प्रेरण B प्राप्त होता है। यदि हम चकती पर रखे गये आवेश की मात्रा और इसके कोणीय वेग को नियत रखें और चकती की त्रिज्या में परिवर्तन करें, तब चकती के केन्द्र पर चुम्बकीय प्रेरण का परिवर्तन इस चित्र द्वारा दर्शाया जाएगा
View SolutionDisk 1 rotates about a smooth vertical axis with the angular velocity omega_(1) . Disk 2 rotating with the angular velocity omega_(2) is kept on disk 1 while rotating in the same direction. Find the change in the rotational kinetic energy of the system given that the moments of inertia of the disks relative to the rotation axis are equal to I_(1)andI_(2) , respectively. The constant surface of the disks are rough.
View SolutionA solid disk rotates in the horizontal plane at an angular velocity of with respect to an axis perpendicular to the disk at its center. The moment of inertia of the disk is . From above, sand is dropped straight down onto this rotating disk, so that a thin uniform ring of sand is formed at a distance of 0.40 m from the axis. The sand in the ring has a mass of 0.50 kg. After all the sand is in place, what is the angular velocity of the disk?
View SolutionA disk with moment of inertia rotates about frictionless, vertical axle with angular speed A second disk, this one having moment of inertia and initial not rotating, drops onto the first disk (Fig.) Because of friction between the surfaces, the two eventually reach the same angular speed . The value of is.
 .View Solution
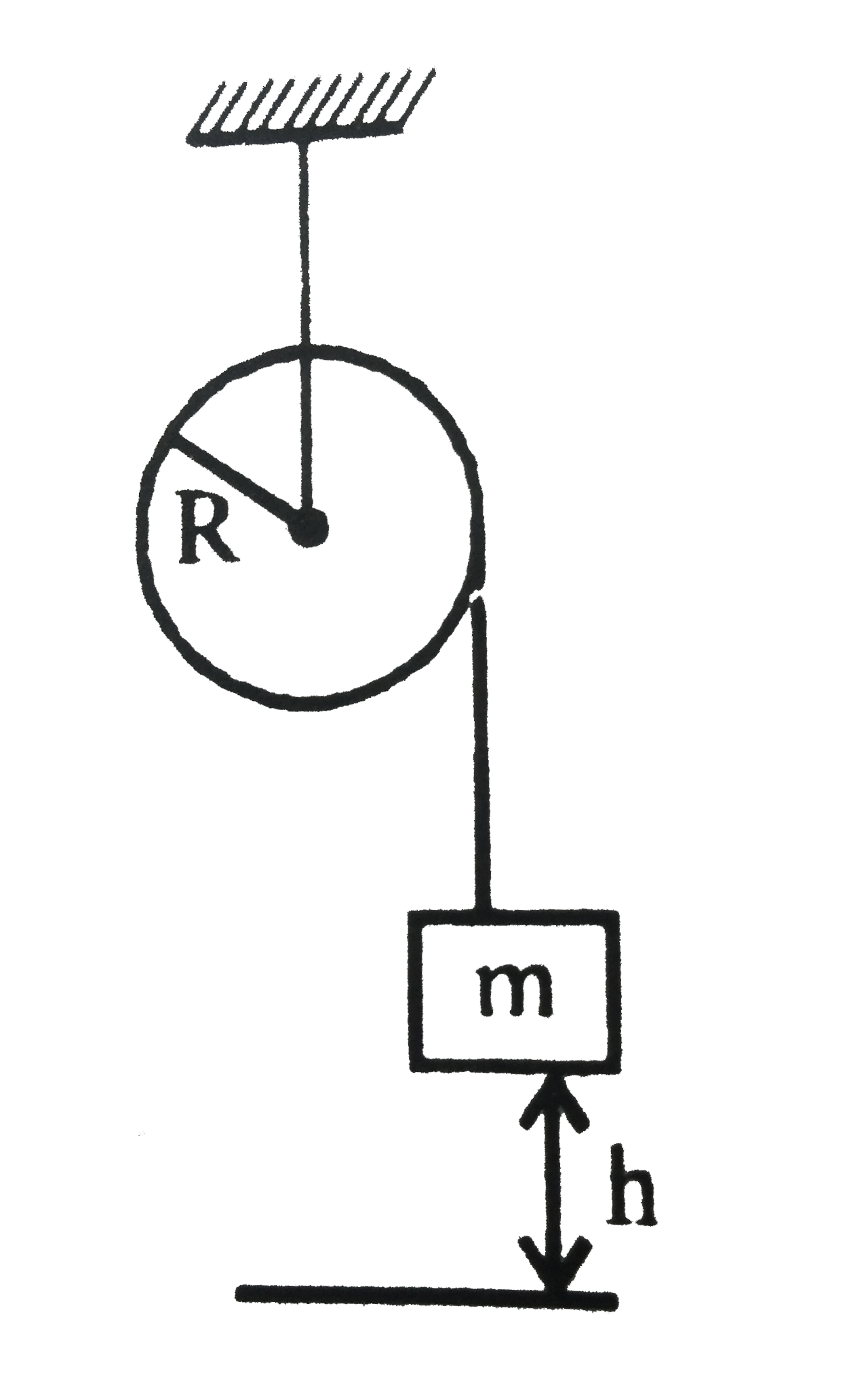
.View SolutionA mass is attached to a pulley through a cord as shown in figure. The pulley is a solid disk with radius . The cord does not slip on the disk. The mass is released from rest at a height from the ground and at the instant the mass reaches the ground, the disk is rotating with angular velocity . Find the mass of the disk.
 .View Solution
.View SolutionA thin circular disk of radius R is uniformly charged with density sigma gt 0 per unit area. The rotates about its axis with a uniform angular speed omega . The magntic moment of the disk is :
View SolutionA cockroach of mass m lies on the rim of a uniform disk of mass 4.00 m that can rotate freely about its center like a merry-goround. Initially the cockroach and disk rotate together with an angular velocity of 0.320 rad/s. Then the cockroach walks halfway to the center of the disk. (a) What then is the angular velocity of the cockroach-disk system? (b) What is the ratio of the new kinetic energy of the system to its initial kinetic energy? ( c) What accounts for the change in the kinetic energy?
View SolutionTwo disks are rotating about the same axis. Disk A has a moment of inertia of and an angular velocity of . Disk B is rotating with an angular velocity of . The two disks are then linked together without the aid of any external torques, so that they rotate as a single unit with an angular velocity of . The axis of rotation for this unit is the same as that for the separate disks. What is the moment of inertia of disk B?
View SolutionA rhinoceros beetle rides the rim of a small disk that rotates like a merry-go-round. If the beetle crawls toward the center of the disk, do the following (each relative to the central axis) increase, decrease, or remain the same for the beetle-disk system: (a) rotational inertia, (b) angular momentum, and ( c) angular speed?
View SolutionA non-conducting disk of radius R is rotating about its own axis with constant angular velocity omega in a perpendicular uniform magnetic field B as shown in figure. The emf induced between centre and rim of disk is
View Solutionअपने अक्ष पर कोणीय चाल से घूर्णन करने वाली किसी चक्रिका को धीरे से ( स्थानांतरीय धक्का दिए बिना ) किसी पूर्णतः घर्षणरहित मेज पर रखा जाता है । चक्रिका की त्रिज्या r है । चित्र में दर्शाई चक्रिका के बिंदुओं A, B तथा C पर रैखिक वेग क्या हैं ? क्या यह चक्रिका चित्र में दर्शाई दिशा में लोटनिक गति करेगी ?
 View Solution
View Solution
