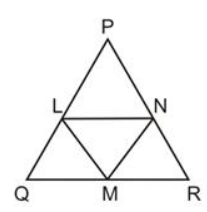
In a ΔPQR if PQ = QR and L M and N are the mid-points of the sides PQ QR and RP respectively. Prove that: LN = MN.
Given that in ΔPQR PQ =QR and L M N are midpoints of the sides PQ QP and RP respectively and given to prove that LN = MNHere we can observe that PQR is and isosceles triangleAnd also L and M are midpoints of PQ and QR respectively∴ ∠QPR and ∠LPN and ∠QRP and ∠MR are samePN=NR [∴ N is midpoint of PR]So by SAS congruence criterion we have ΔLPN≅ΔMRN⇒ LN=MN[∴ Corresponding parts of congruent triangles are equal]
Related Solutions
में, यदि PQ=QR तथा L,M और N क्रमशः भुजाओं PQ,QR और RP के मध्य बिन्दु हो, तो सिध्द करो कि LN=MN है |
View SolutionIn A if are the mid-points of the sides respectively. Prove that
View SolutionIn trianglePQR , S is the point on the side QR. Prove that PQ+QR+RP>2PS
View SolutionM and N are mid- point on sides QR and PQ respectively of , right-anggled at Q. Prove that :
.
View SolutionM and N are mid point on sides QR and PQ respectively of , right-anggled at Q. Prove that :
.
View SolutionM and N are points on the sides PQ and PR respectively of . If PQ = 1.28 PR = 2.56, PM = 0.16 and PN = 0.32, prove that MN || QR.
View SolutionIf S is the mid-point of side QR of a , then prove that .
View SolutionIf S is the mid-point of side QR of a , then prove that .
View SolutionIf S is the mid-point of side QR of a , then prove that .
View SolutionIf S is the mid-point of side QR of a , then prove that .
View SolutionIf S is the mid-point of side QR of a , then prove that .
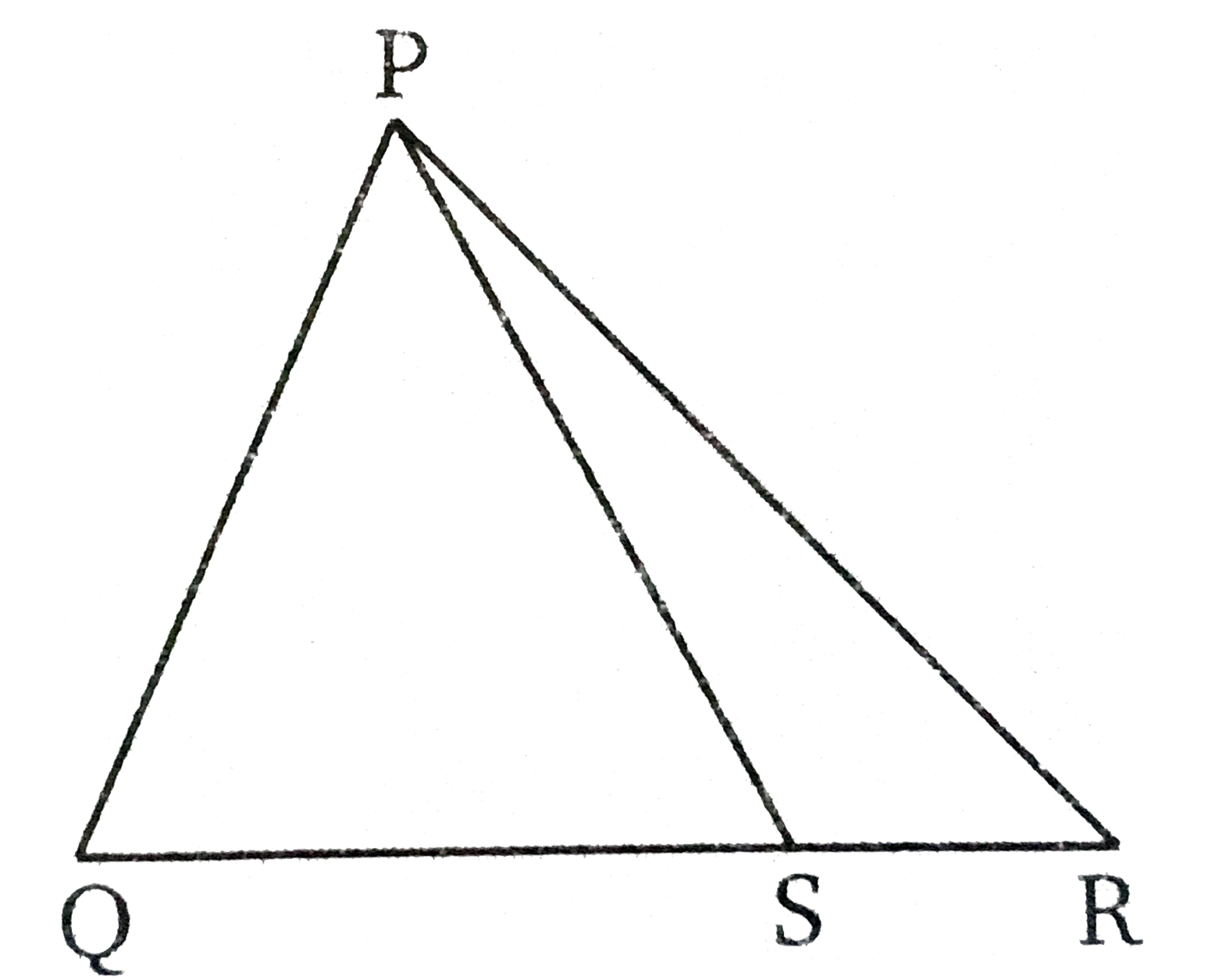
View SolutionIn the adjoining figure, point S is on side QR of . Prove that
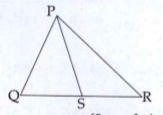
View SolutionIn the figure triangle PQR Prove that if S is any one point on the side QR, PQ+QR+RP gt 2PS
View Solutionदिये गये चित्र में , की भुजा QR पर कोई बिंदु है तो सिद्ध कीजिए कि
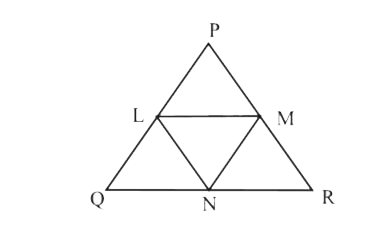
View SolutionIn the given figure L, M and N are mid point of the sides PQ, PR and QR respectively of . If PQ = 4.4 cm, QR = 5.6 cm and PR = 4.8 cm then find the perimeter of .
View SolutionSimplify the following : (p+q+r)(pq+qr+rp)+(pq+qr)
View SolutionIn , M and N are two points on PQ and PR such MN || QR and PM = 1/2 QM. If QR = 4.5cm. Then MN =
View SolutionIn the adjoining figure, is formed by the sides PQ, QR and RP which are drawn parallel to sides AB,BC and CA respectively of Prove that

View SolutionIn the adjoining figure, is formed by the sides PQ, QR and RP which are drawn parallel to sides AB,BC and CA respectively of Prove that

View SolutionLet be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
View Solution