The feasible region for a LPP is shown in Fig. 12.9. Find the minimum value of Z = 11x + 7y.
Hence the minimum value of Z is 21 at 0 3
Related Solutions
The feasible region for LPP is shown shaded in the figure . Find the minimum value of the objective function z = 11x + 7y.
View SolutionThe feasible region for an LPP is shown in following figure. Find the minimum value of

View SolutionThe feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.

View SolutionThe feasible region for a LPP is shown in Figure. Find the minimum value of .
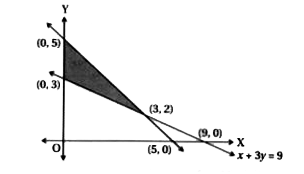
View SolutionThe feasible region for an LPP is show shaded in the figure 12.45 find the minimum value of the objective function Z=11x+7y.
View SolutionThe feasible region of an LPP is shown in the figure. If , thent he maximum value of Z occurs at

View SolutionFeasible region (shaded) for a LPP is shown in Figure Maximise z = 5x + 7y.
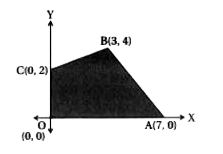
View SolutionThe feasible region for an LPP is shown shaded in the figure 12.48 find the minimum value of Z=4x+y.
View SolutionThe feasible region for a LPP is shown in the following figure. Evaluate Z=4x+y at each of the corner points of the region. Find the minimum value of Z, if it exists

View SolutionThe feasible region for a LPP is shown in Figure. Evaluate z = 4x + y at each of the corner points at this region. Find the minimum value of z, if exists.

View SolutionThe feasible region for a LPP is shown in the following figure. Evaluate Z=4x+y at each of the corner points of the region. Find the minimum value of Z, if it exists

View SolutionThe feasible region of an LPP is shown in the figure. If z = 3x + 9 y , then the minimum value of z occurs at
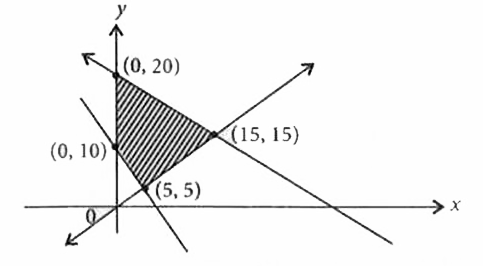
View SolutionThe feasible region of an LPP is shown in the figure. If ,then the minimum value of z occurs at
View Solutionकिसी LPP का सुसंगत क्षेत्र आकृति में प्रदर्शित है। Z = 11x +7y का न्यूनतम मान ज्ञात कीजिए।

View SolutionThe feasible solution for a LPP is shown in Fig. Let. Z = 3x-4 y be the objective function. Minimum value of F is
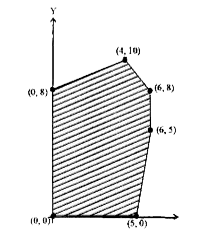
View SolutionIn the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of
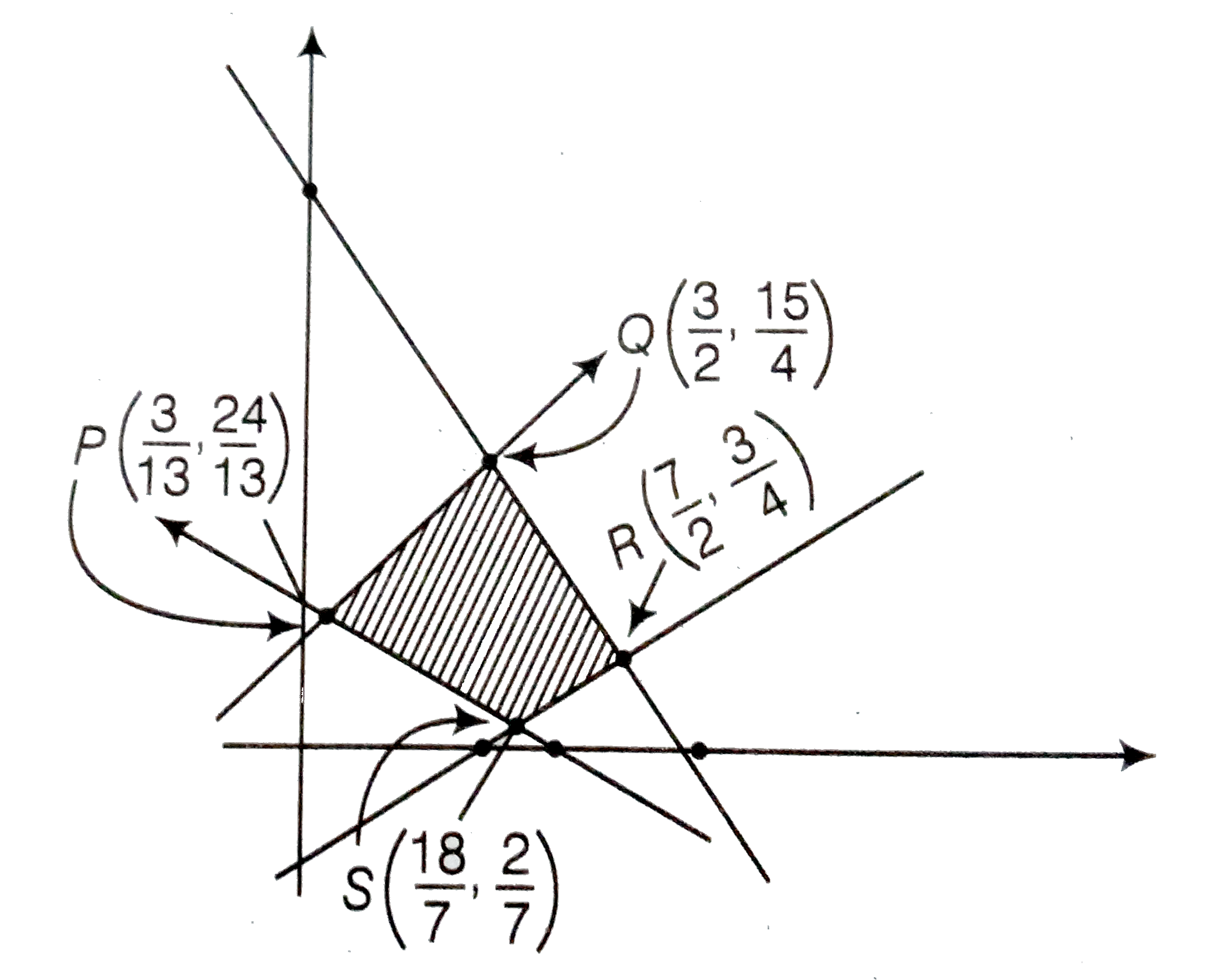
View SolutionThe feasible region for an LPP is shown shaded in the figure 12.47. Determine the maximum and minimum values of Z=x+2y.
View SolutionIn Figure, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of z = x + 2y.
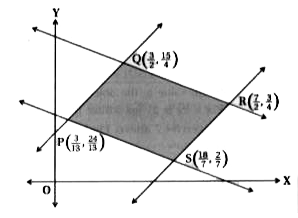
View SolutionIn the following figure, the feasible region for a LPP is shown.
Determine the maximum and minimum value of
.
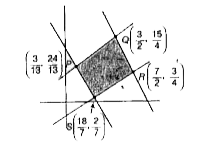
View SolutionDetermine the minimum value of (if any), if the feasible region for an LPP is shown in figure:
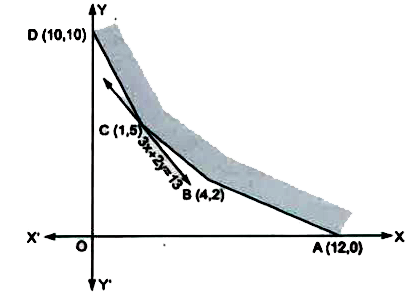
View Solution