ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that i D is the mid-point of AC. ii MD ⊥ AC iii CM = MA = 1/ 2 AB
Given : A triangle ABC in which ∠C = 90° and M is the mid-point of AB and BC || DM. To Prove : i D is the mid-point of AC [Given] ii DM ⊥ BC iii CM = MA = 1/ 2 AB Construction : Join CM. Proof : i In ∆ABC M is the mid-point of AB. [Given] BC || DM [Given] D is the mid-point of AC [Converse of mid-point theorem] Proved. ii ∠ADM = ∠ACB [∵ Coresponding angles] But ∠ACB = 90° [Given] ∴ ∠ADM = 90° But ∠ADM + ∠CDM = 180° [Linear pair] ∴ ∠CDM = 90° Hence MD ⊥ AC Proved. iii AD = DC …1 [∵ D is the mid-point of AC] Now in ∆ADM and ∆CMD we have ∠ADM = ∠CDM [Each = 90°] AD = DC [From 1] DM = DM [Common] ∴ ∆ADM ≅ ∆CMD [SAS congruence] ⇒ CM = MA …2 [CPCT] Since M is mid-point of AB ∴ MA = 1/ 2 AB …3 Hence CM = MA = 1 /2 AB Proved. [From 2 and 3]
Related Solutions
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that .
View SolutionABC is a triangle right angled at C and M is mid-point of hypotenuse AB. Line drawn through M and parallel to BC intersects AC at D. Show that:
MD is mid-point of AC.
View Solutionएक त्रिभुज है जिसका कोण समकोण है। कर्ण के मध्य - बिंदु से होकर के समांतर खींची गई रेखा को पर प्रतिच्छेद करती है। दर्शाइए कि
(i) भुजा का मध्य - बिंदु है। (ii ) है
(iii) है।
View SolutionABC is a triangle right angled at C. A line through the mid points M of hypotenuse AB and parallel to BC intersects AC at D. Show that
D is the mid point of AC
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
D is the mid-point of AC
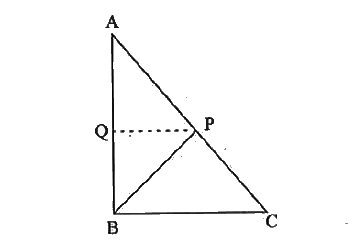
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that D is the mid-point of AC.
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that CM = MA = .
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
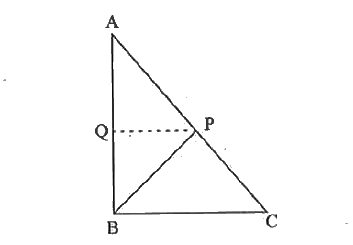
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that D is the mid-point of AC.
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that

View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that (i) D is the mid-point of AC (ii) (iii)
View SolutionABC is a triangle right-angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii)
(iii)
View SolutionABC is a triangle right angled at 'C'. A line through the midpoint M of hypotenuse AB and parallel to BC intersects AC at D. Show that : D is the midpoint of AC.
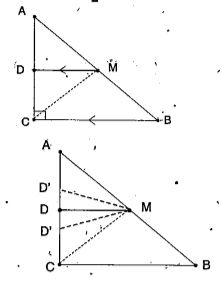
View SolutionABC is a triangle right angled at C. A line through the midpoint M of hypotenuse AB and parallel to BC Intersects AC at D. Show that :
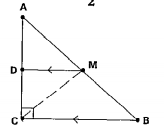
View SolutionABC is a triangle right angled at 'C'. A line through the midpoint M of hypotenuse AB and parallel to BC intersects AC at D. Show that : CM = MA = 1/2 AB .
View SolutionABC is a right angle in a right triangle ABC. Prove the following if the line drawn parallel to BC through the midpoint M of hypotenuse AB intersects AC at D. CM=MA = 1/2 AB
View SolutionABC is a triangle right angled at C. A line through the midpoint M of hypotenuse AB and Parallel to BC intersects AC at D. Show that
(i) D is the midpoint of AC
(ii)
(iii)
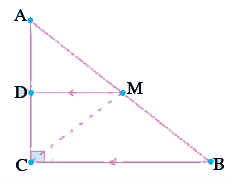
View SolutionABC is a triangle right angled at C. A line through the midpoint M of hypotenuse AB and Parallel to BC intersects AC at D. Show that
(i) D is the midpoint of AC
(ii)
(iii)
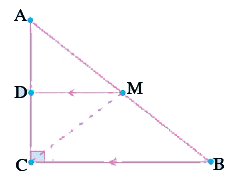
View SolutionABC is a triangle right angled at C. A line through the midpoint M of hypotenuse AB and Parallel to BC intersects AC at D. Show that
(i) D is the midpoint of AC
(ii)
(iii)
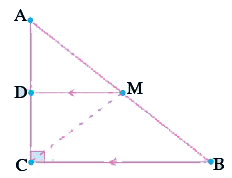
View SolutionABC is a right angle in a right triangle ABC. Prove the following if the line drawn parallel to BC through the midpoint M of hypotenuse AB intersects AC at D. MD _|_ AC
View Solution