ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that (i) D is the mid-point of AC (ii) MD⊥AC (iii) CM=MA=12AB
To solve the problem step by step, we will address each part of the question sequentially.
Given:
- Triangle ABC is right-angled at C.
- M is the midpoint of hypotenuse AB.
- A line through M is parallel to BC and intersects AC at D.
To Prove:
1. D is the midpoint of AC.
2. MD ⊥ AC.
3. CM = MA = 1/2 AB.
Step 1: Proving D is the midpoint of AC
1. Identify the properties:
- M is the midpoint of AB.
- MD is parallel to BC.
2. Use the Midpoint Theorem:
- According to the Midpoint Theorem, if a line segment is drawn from the midpoint of one side of a triangle parallel to another side, it bisects the third side.
- Here, since M is the midpoint of AB and MD is parallel to BC, it follows that D must be the midpoint of AC.
Conclusion for Step 1:
Thus, we have shown that D is the midpoint of AC.
- Triangle ABC is right-angled at C.
- M is the midpoint of hypotenuse AB.
- A line through M is parallel to BC and intersects AC at D.
1. D is the midpoint of AC.
2. MD ⊥ AC.
3. CM = MA = 1/2 AB.
- M is the midpoint of AB.
- MD is parallel to BC.
- According to the Midpoint Theorem, if a line segment is drawn from the midpoint of one side of a triangle parallel to another side, it bisects the third side.
- Here, since M is the midpoint of AB and MD is parallel to BC, it follows that D must be the midpoint of AC.
Thus, we have shown that D is the midpoint of AC.
Topper's Solved these Questions
Similar Questions
ABC is a triangle right angled at C and M is mid-point of hypotenuse AB. Line drawn through M and parallel to BC intersects AC at D. Show that:
MD is mid-point of AC.
View SolutionΔABC is a right triangle right angled at A such that AB=AC and bisector of ∠C intersects the side AB at D. Prove that AC+AD=BC.
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
CP=12AB
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
ΔDBC≅ΔACB
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
ΔAPC≅ΔBPD
View SolutionIn right triangle ABC , right angle at C, M is the mid-point of the hypotenuse AB. C is jointed to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that AMC≅BMD (ii) ∠DBC=∠ACB DBC≅ACB (iii) CM=12AB
View SolutionIf D is the mid-point of the hypotenuse AC of a right triangle ABC, prove that BD=12AC
View SolutionIn right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC≅ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC≅ΔACB
(iv) CM=12AB
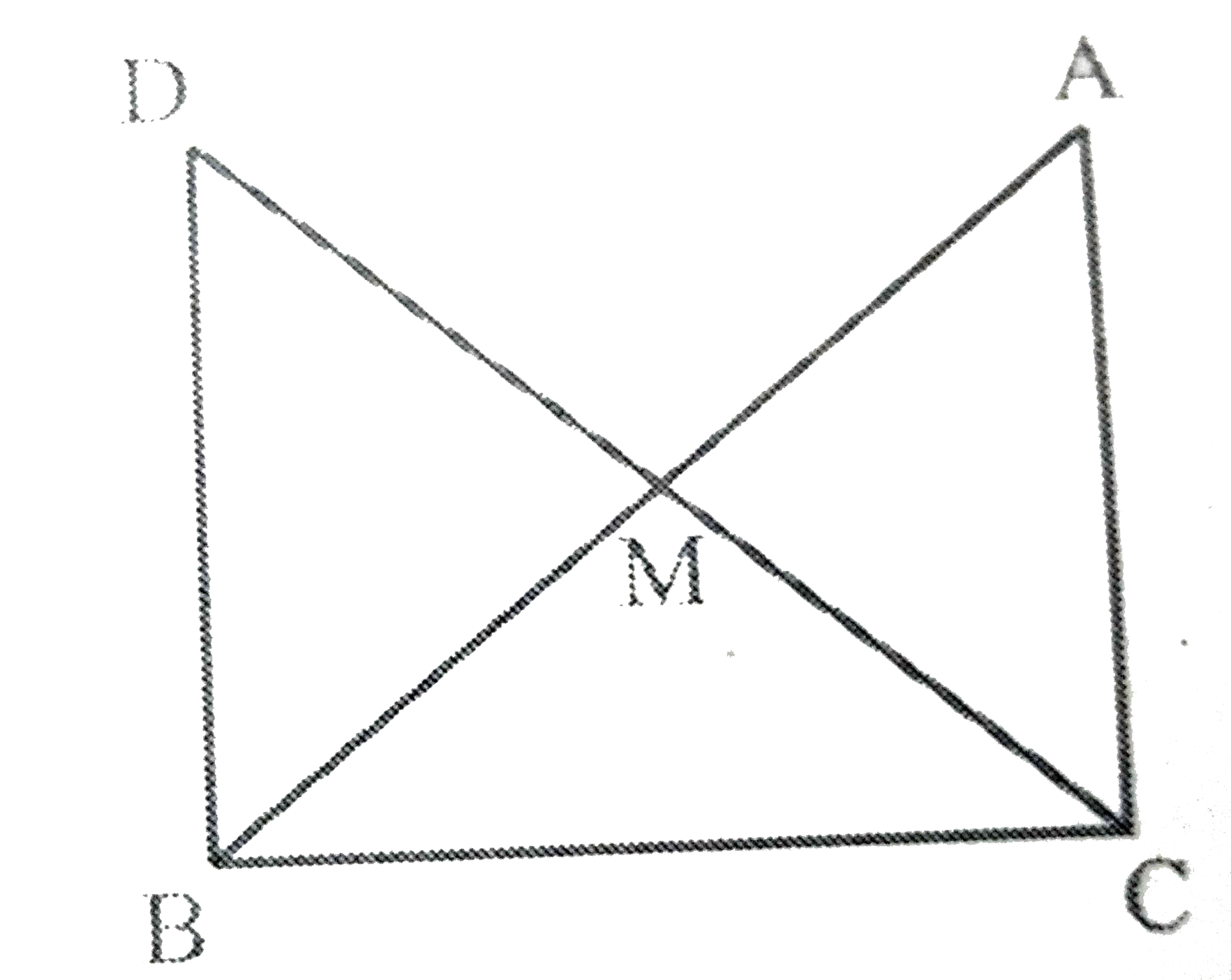
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.
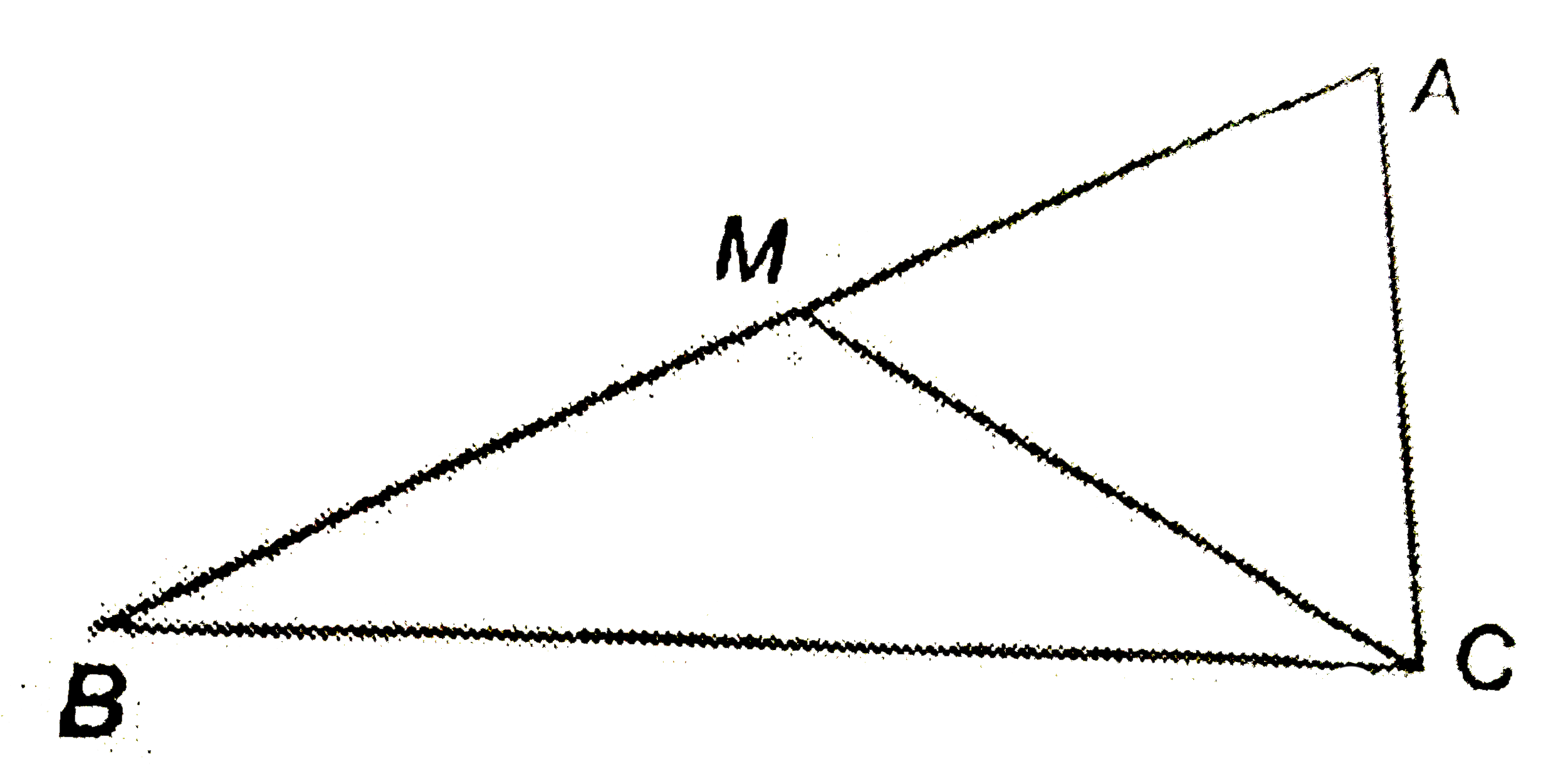
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
Angle DBC is a right angle.
View Solution
