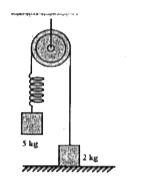
System shown in the figure is released from rest when spring is unstretched. Pulley and spring is mass less and friction is absent everywhere. The speed of 5 kg block when 2 kg block leaves the contact with ground is Take force constant of spring k = 40 N/m and g =10 m/s2 A √2 m/sB 2√2 m/sC 2 m/sD 4√2 m/s
Correct Answer is: B 2√2 m/s20 = kxx = 1/2 m5 × 10 × 1/2 - 1/2 k 1/22 v2 ⇒ 25 - 20 1/22= 1/2 v2v = 2√2 m/s
Related Solutions
System shown in figure is released from rest . Pulley and spring is mass less and friction is absent everywhere. The speed of block when block leaves the constant of with ground is (force constant of spring

View SolutionSystem shown in figure is released from rest . Pulley and spring is massless and friction is absent everywhere. The speed of block when block leaves the contact with ground is (force constant of spring

View SolutionThe system shown in the diagram is released from rest. In this pulley, string and spring are massless and the friction is absent everywhere. The speed of 5 kg block, when 2 kg block removes the contact with the ground is (force constant of the spring K = 40 N m^(-1) and g = 10 ms^(-2))
View SolutionThe system shown in Fig. is released from rest with mass 2 kg in contact with the ground. Pulley and spring are massless, and friction is absent everywhere. The speed of 5 kg block when 2 kg block leaves the contact with the ground.is (force constant of the spring )
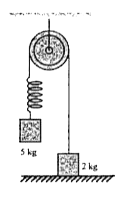
View SolutionThe system shown in the figure is released from rest along the original length of the spring and the wire is taut. Pulley and spring are massless and friction is absent everywhere. spring constant value k = "40 N m"^(-1) Is. What will be the speed of a 5 kg block when the 2 kg block loses contact with the support below?
View SolutionA 2 kg block is connected with two springs of force constants k_(1)=100 N//m and k_(2)=300 N//m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10 m//s^(2))
View SolutionA 2 kg block is connected with two springs of force constants k_(1)=100 N//m and k_(2)=300 N//m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10 m//s^(2))
View SolutionSystem shown in figure is released from rest. Pulley and spring are massless and friction is absent every where. The speed of 5 kg block when 2 block leaves a contact with ground is

View SolutionThe system in fig is released from rest with mass 2 kg in contact with the ground pulley and spring are massless and friction is absent every where . The speed of 5kg block when 2 kg block leaves the contact with the ground is ( foroce cosntant of the spring and
View SolutionIn the figure shown, the system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N/m.
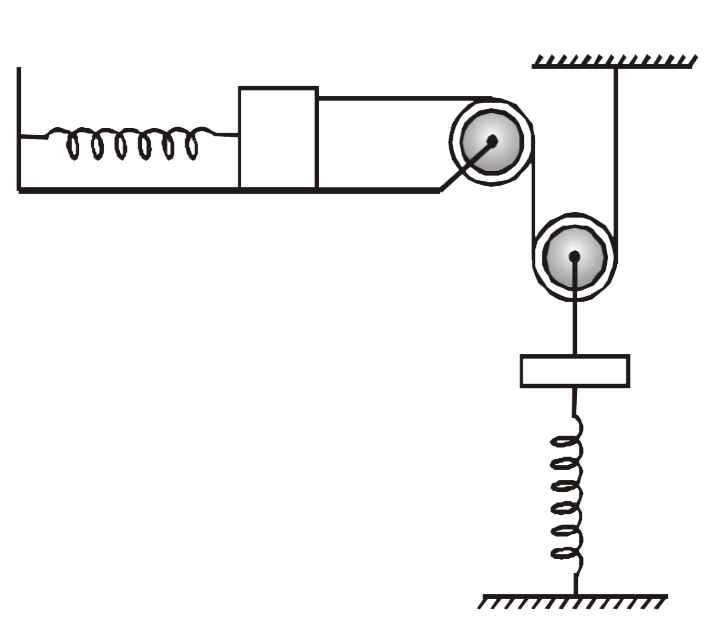
Maximum speed of the block placed horizontally is:
View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10 m//s^(2) . Neglect friction
View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10 m//s^(2) . Neglect friction
View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10 m//s^(2) . Neglect friction
View SolutionA 2kg block is connected with two springs of force constants N/m and N/m as shown in figure. The block is released from rest with the springs unstretched. Find the acceleration of the block in its lowest position

View SolutionA block of mass 20 kg is hung with the help of ideal string, pulleys and spring (Spring constant k = 1000 N/m) as shown in figure. If block is in equilibrium position then extension in the spring will be (g = 10 ms^-2)
View SolutionForce constant of a spring is 100 N//m . If a 10kg block attached with the spring is at rest, then find extension in the spring. ( g= 10 m//s^(2) )
View SolutionConsider the situation shown in figure. Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find (a) The maximum extension of the spring x_(m) (b) The speed of block A when the extension in the springt is x=(x_(m))/(2) (c ) The net acceleration of block B when extension in the spring is x=(x_(m))/(4).
View SolutionConsider the situation shown in figure. Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find (a) The maximum extension of the spring x_(m) (b) The speed of block A when the extension in the springt is x=(x_(m))/(2) (c ) The net acceleration of block B when extension in the spring is x=(x_(m))/(4).
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is and force constant of each spring is . Then choose the incorrect option(s). Assume puleys and strings are massless and all contacts are smooth.
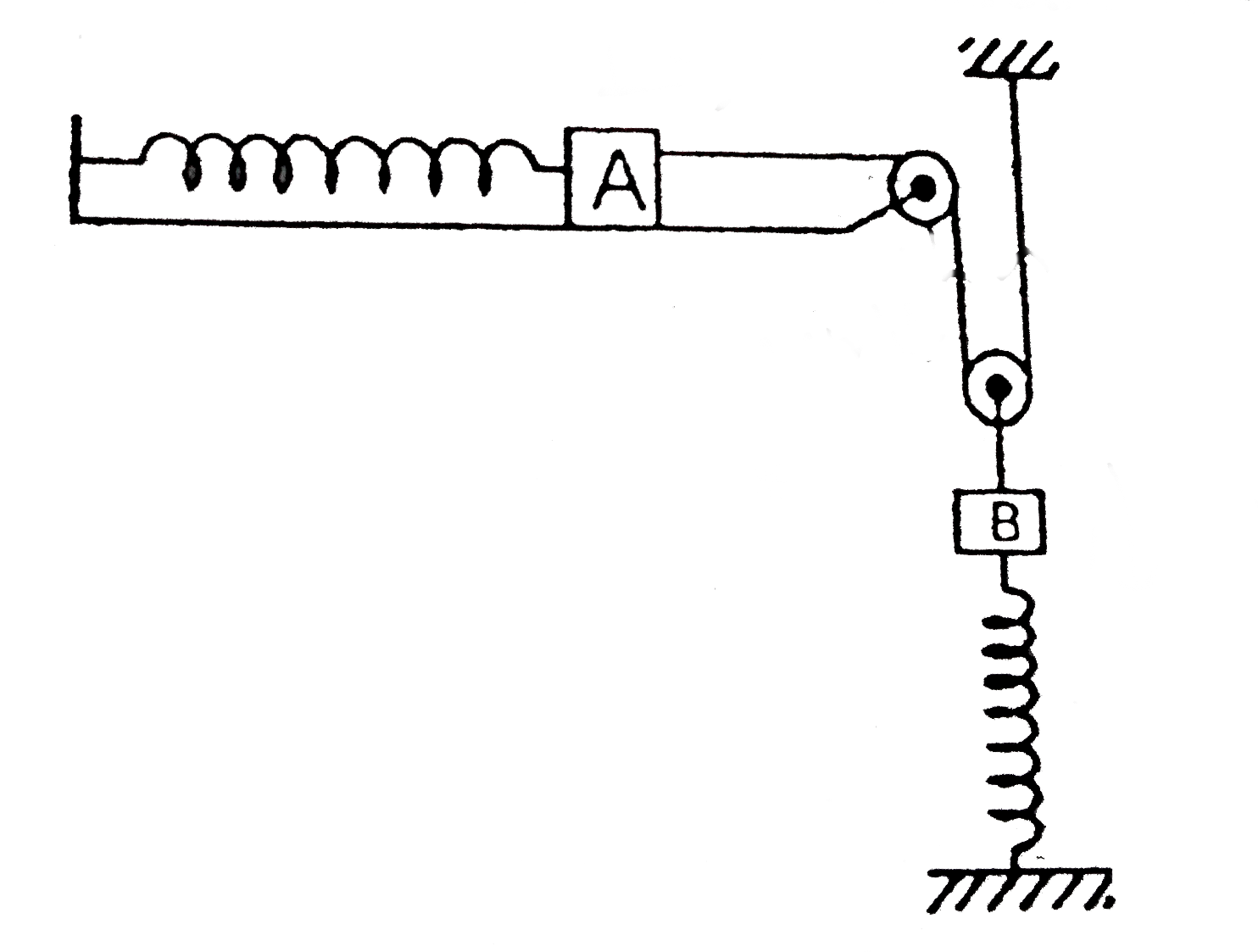
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N//m . Then choose the incorrect option(s). Assume puleys and strings are massless and all contacts are smooth. (g = 10 m//s^(2))
View Solution