The system is released from rest with both the springs in unstretched positions. Mass of each block is 1kg and force constant of each spring is 10N/m. Then choose the incorrect option(s). Assume puleys and strings are massless and all contacts are smooth. (g=10m/s2)
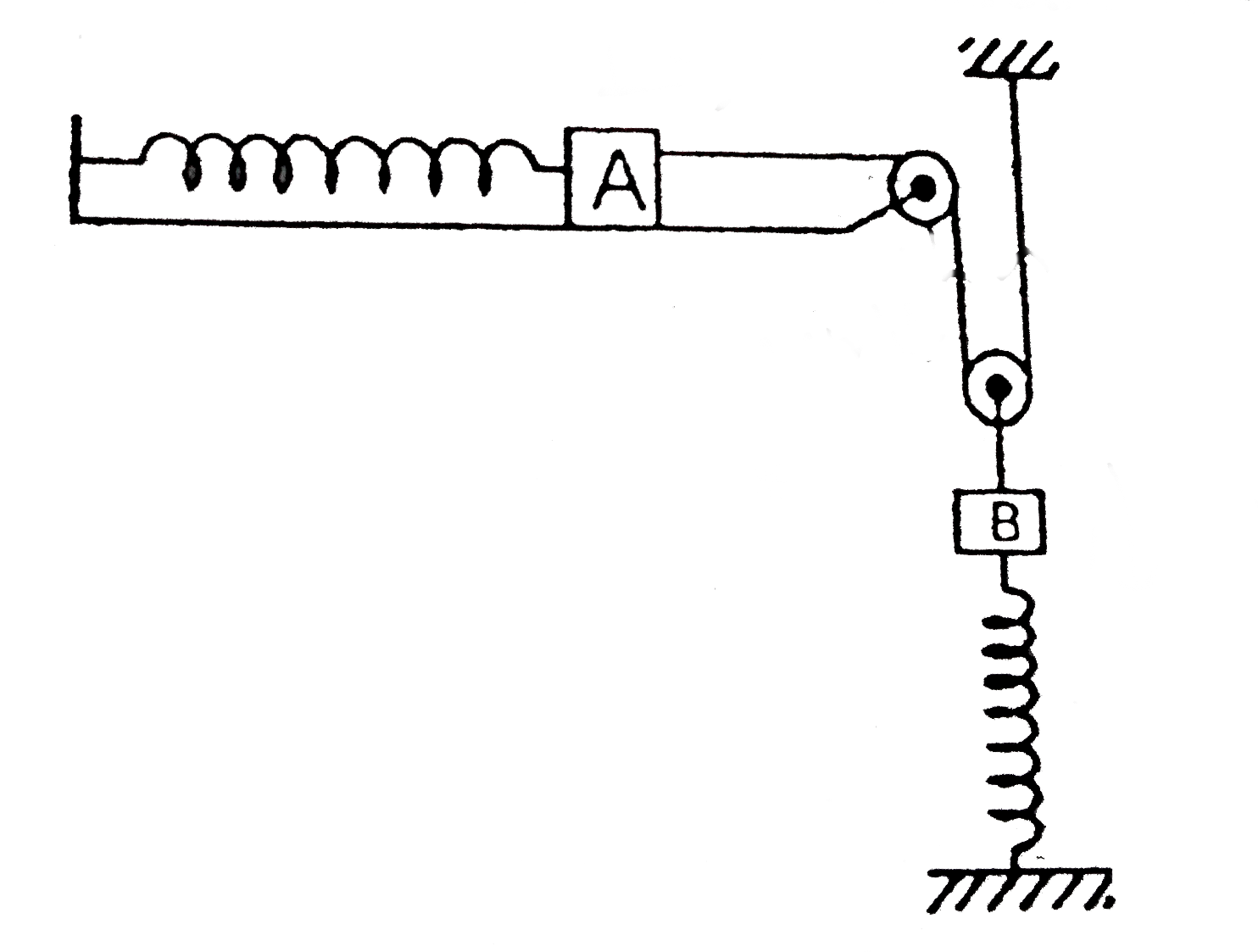
Extension of horizontal spring in spring in equilibrium is 0.4m
Extension of horizontal spring in spring in equilibrium is 0.2m
Maximum speed of the block A is 8m/s
Maximum speed of the block A is 12m/s
The correct Answer is:B, C, D

3kx=mg
√x10×x=1×10
x=15=0.2
(ii)(1)(g)(x)
=12(1)(v)2+12(1)(2v)2x+12(10)(0.2)2+12(10)(0.4)2
2=V22(1+4+0.4+1.6)
v2=4×7
v=2√7
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 2
20 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
The system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
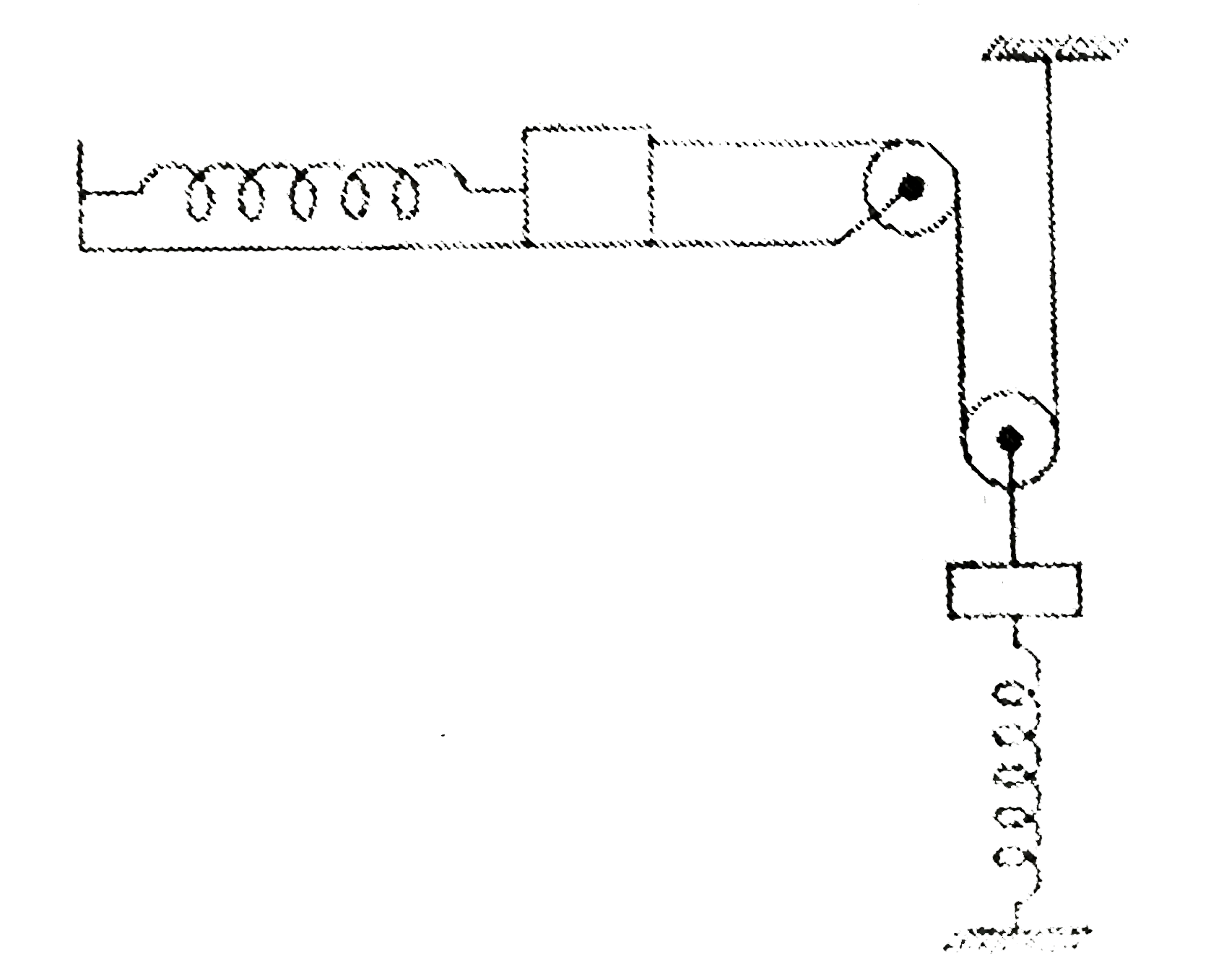
Extension of horizontal spring in equilibrium is
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
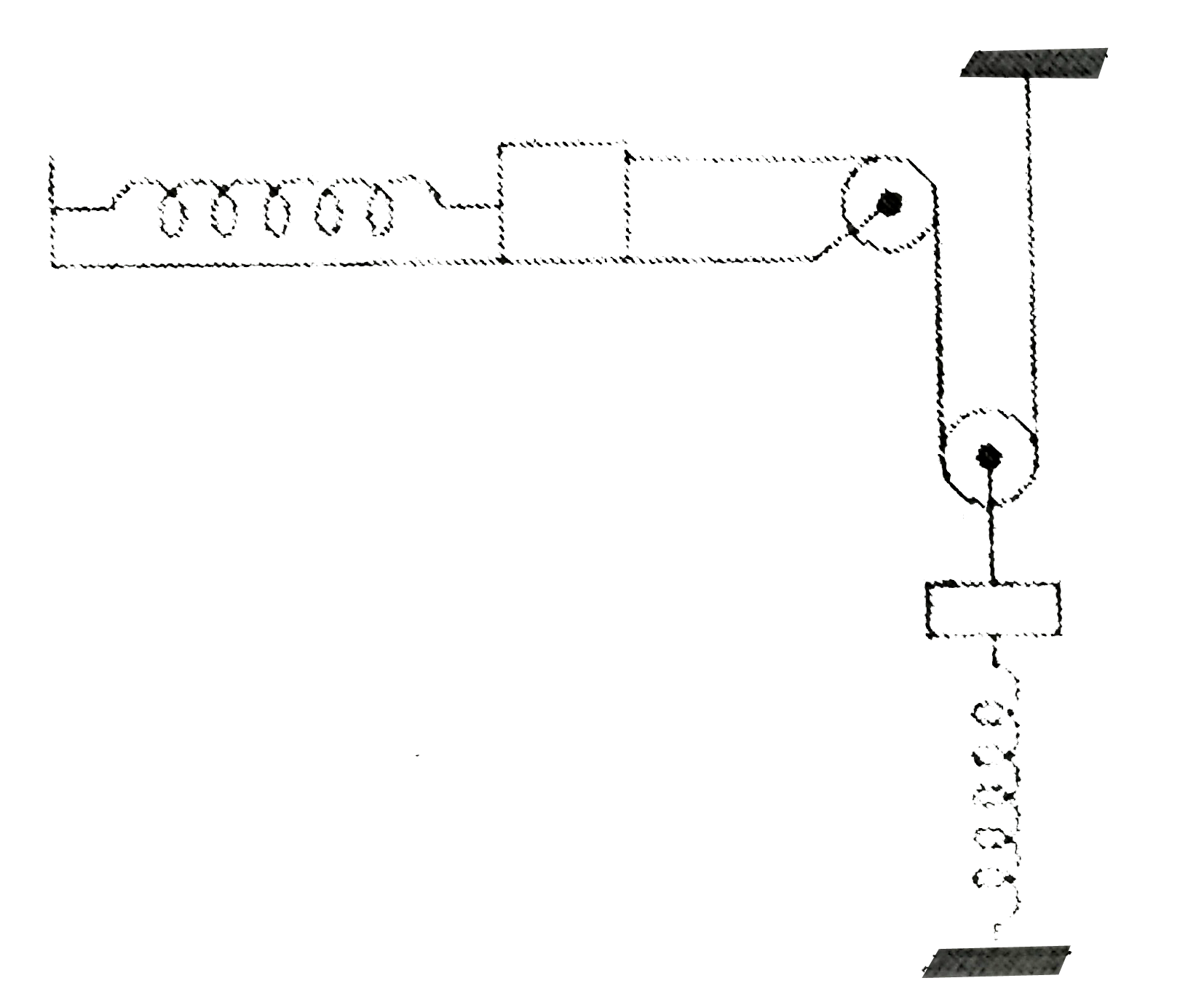
In the equilibrium position, speed of the block placed horizontally is
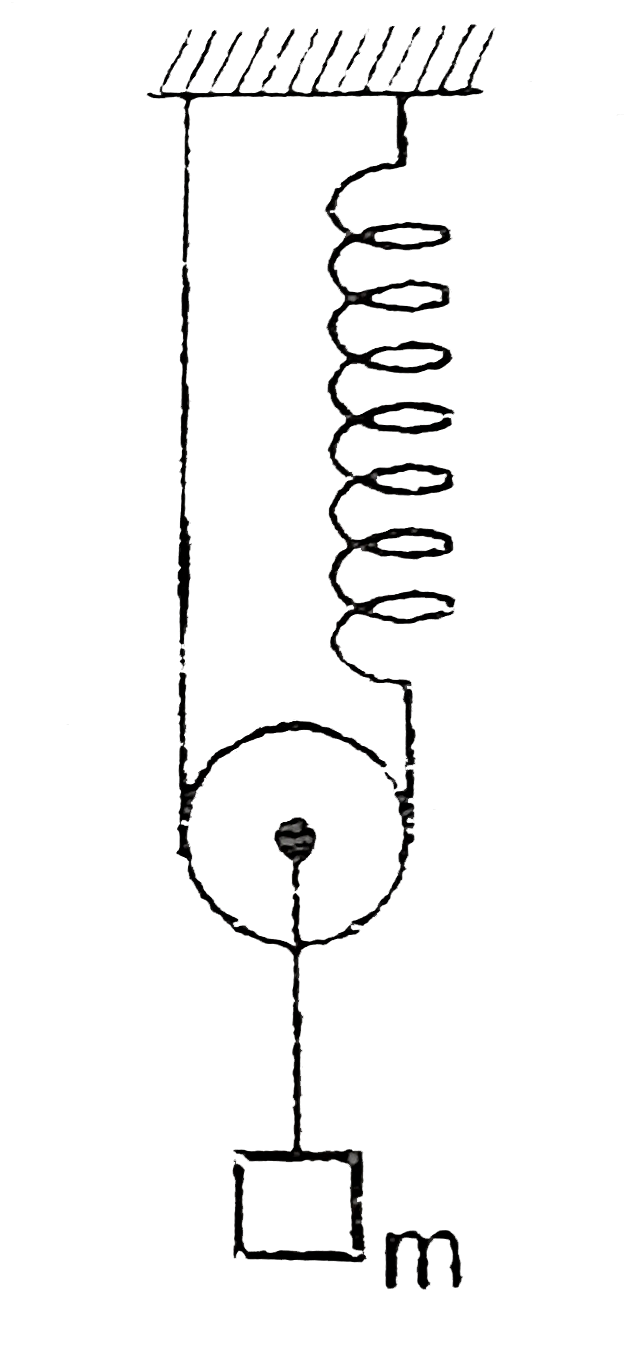
View SolutionThe system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k=100N/m, then maximum extension in spring is :
View SolutionIf the force constant of spring is 50Nm−1, find mass of the block, if it an rests in the given situation (g=10ms−2).

View SolutionIn the given figure, Find mass of the block A, if it remains at rest, when the system is released from rest. Pulleys and strings are massless. [g=10m/s2]

View SolutionA mass m = 8kg is attached to a spring as shown in figure and held in positioin so that the spring remains unstretched. The spring constant is 200 N/m. The mass m is then released and begins to undergo small oscillations. The maximum velocity of the mass will be (g=10m/s2)
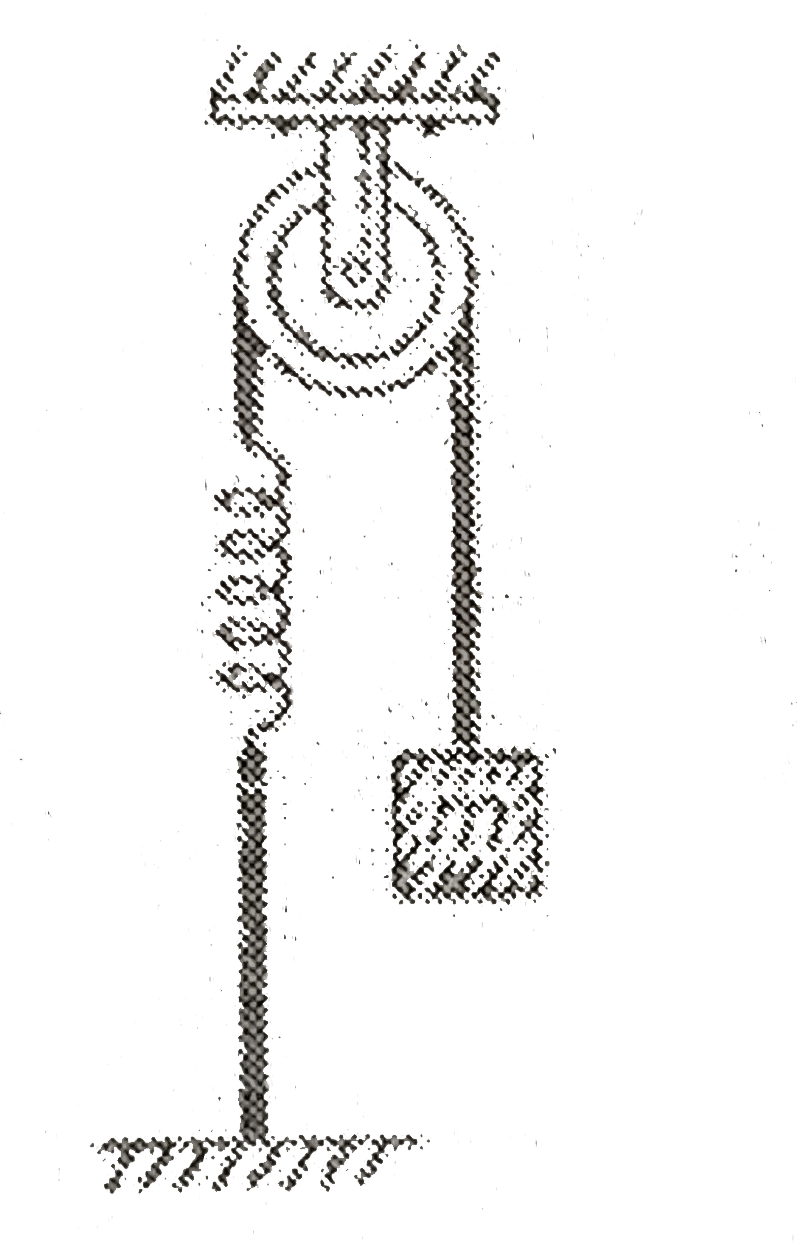
View SolutionA block of mass 4 kg is released from the top of an inclined smooth surface as shown in figure If spring constant of spring is 100N/m and block comes to rest after compressing spring by 1 m, find the distance travelled by the block before it comes t o rest.

View SolutionSystem shown in figure is released from rest . Pulley and spring is mass less and friction is absent everywhere. The speed of 5kg block when 2kg block leaves the constant of with ground is (force constant of spring k=40N/mandg=10m/s2)

View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is

View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is

View Solution
