A block of mass 20 kg is hung with the help of ideal string, pulleys and spring (Spring constant k = 1000 N/m) as shown in figure. If block is in equilibrium position then extension in the spring will be (g=10ms−2)
10 cm
2.5 cm
5 cm
20 cm
The correct Answer is:D
To solve the problem of finding the extension in the spring when a block of mass 20 kg is in equilibrium, we can follow these steps:
Step 1: Identify the forces acting on the block
When the block is in equilibrium, the forces acting on it are:
- The gravitational force (weight) acting downwards, which is given by mg.
- The spring force acting upwards, which is given by Hooke's law as kx, where x is the extension in the spring.
Step 2: Write the equilibrium condition
In equilibrium, the net force acting on the block is zero. Therefore, we can write the equation:
mg−kx=0
This implies that:
mg=kx
Step 3: Substitute the known values
We know:
- Mass m=20kg
- Gravitational acceleration g=10m/s2
- Spring constant k=1000N/m
Now substituting these values into the equation:
20kg×10m/s2=1000N/m×x
This simplifies to:
200N=1000N/m×x
Step 4: Solve for the extension x
To find x, we rearrange the equation:
x=200N1000N/m=0.2m
Step 5: Convert to centimeters
Since the question asks for the extension in centimeters:
x=0.2m=20cm
Final Answer
The extension in the spring when the block is in equilibrium is 20 cm.
---
When the block is in equilibrium, the forces acting on it are:
- The gravitational force (weight) acting downwards, which is given by mg.
- The spring force acting upwards, which is given by Hooke's law as kx, where x is the extension in the spring.
In equilibrium, the net force acting on the block is zero. Therefore, we can write the equation:
mg−kx=0
This implies that:
mg=kx
We know:
- Mass m=20kg
- Gravitational acceleration g=10m/s2
- Spring constant k=1000N/m
20kg×10m/s2=1000N/m×x
This simplifies to:
200N=1000N/m×x
To find x, we rearrange the equation:
x=200N1000N/m=0.2m
Since the question asks for the extension in centimeters:
x=0.2m=20cm
The extension in the spring when the block is in equilibrium is 20 cm.
Similar Questions
A block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.
 View Solution
View SolutionA block of mass 5kg is hung with the help of light string which is passing over an ideal pulley as shown as in figure.The force is exerted by the clamp on the pulley will be (g= 10 m/s^2)
_PHY_E05_165_Q01.png) View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Natural length of a spring is 60 cm and its spring constant is 4000 N/m. A mass of 20 kg is hung from it. The extension produced in the spring is (Take, g=9.8m/s2)
A4.9 cmB0.49 cmC9.4 cmD0.94 cm
A block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction
 View Solution
View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction
 View Solution
View SolutionA block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
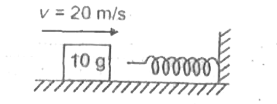 View Solution
View SolutionA block of mass m is attached with a spring in vertical plane as shown in the figure. If initially spring is in its natural length and the block is released from rest, then maximum extension in the spring will be
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.
 View Solution
View SolutionA block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?
 View Solution
View SolutionA block of mass m is suspended by different springs of force constant shown in figure.
 View Solution
View Solution

