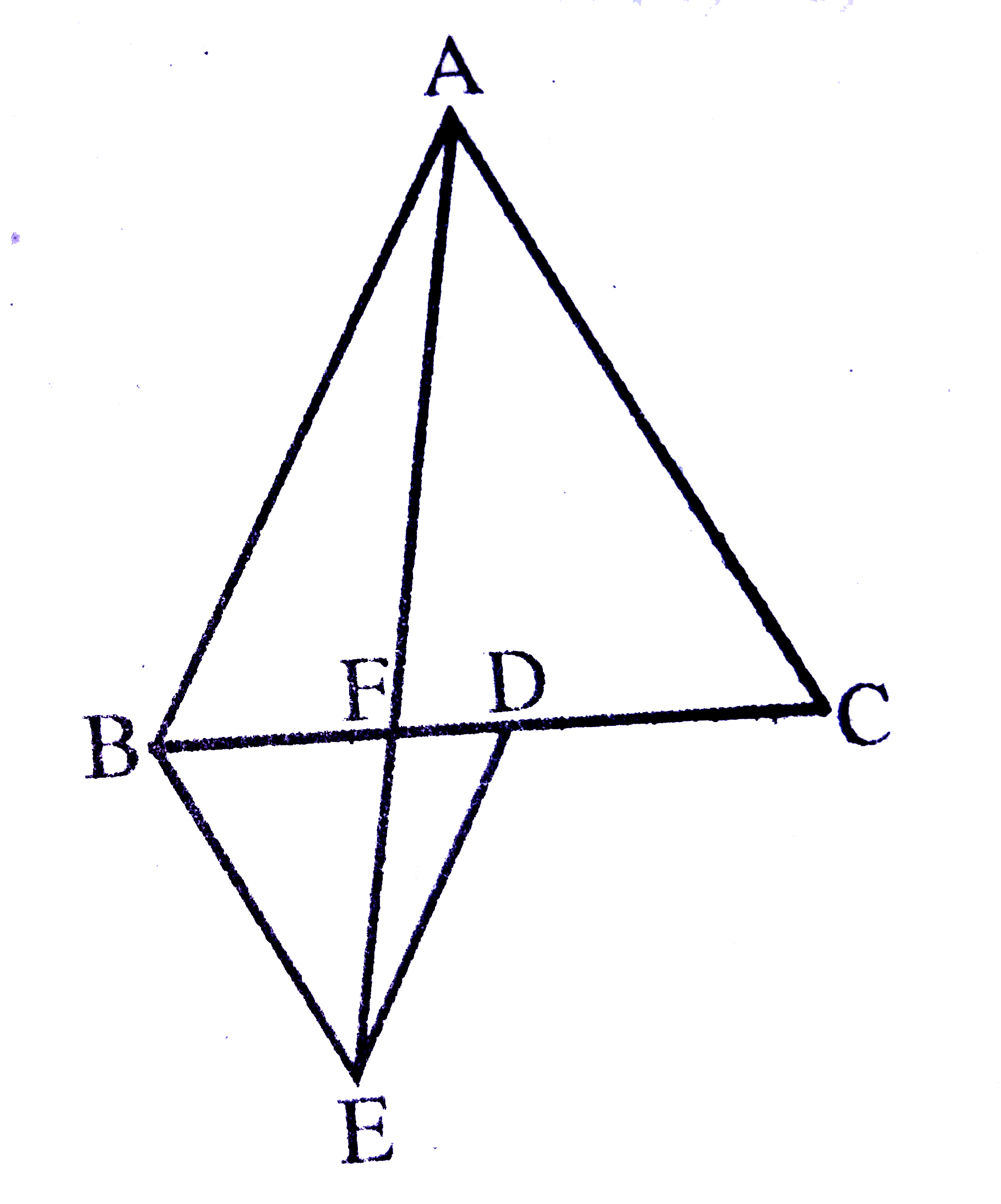
दिए गए आकृति में ABC और BDF दो समबाहु त्रिभुज इस प्रकार है की D भुजा BC का मध्य बिंदु है |यदि AE भुजा BC को F पर प्रतिच्छेद करती है तो दर्शाई की
ar(BDF)=14ar(ABC)
(ii) ar(BDE)=12ar(BAE) ltBrgt (iii) ar(ABC)=2ar(BEC)
(iv) ar(BEF)=ar(AFD) ltBrgt (v) ar(BEF)=2ar(FED)
(vi)ar(FED)=18ar(AFC)
EC तथा AD को मिलाया चुकी ∠1=∠2=60∘
और ये एकांतर कोणों का युग्म है|
∴BE∣∣AC
उसी तरह ED∣∣BA
चूँकि ΔBCE तथा ΔABE एक ही आधार BE पर स्थित है तथा एक ही समांतर रेखाओं BE और AC के बिच स्थित है |
∴ ar(ΔBCE)=ar(ΔBAE) ...(1)
चूँकि D ,BC का मध्य बिंदु है
∴ ar(ΔBAE)=12ar(ΔBCE)
⇒ 2ar(ΔBDE)=ar(ΔBAE)
⇒ ar(ΔBDE)=12ar(ΔBAE) ltBrgt चूँकि ΔBDE तथा ΔAED एक ही आधार पर ED स्थित है तथा एक ही समांतर रेखाओं ED और AB की बिच है|
∴ ar(ΔBDE)=ar(ΔAED) ...(iv)
(iii ) तथा (iv ) को जोड़ने ,पर हमें मिलता है
3ar(ΔBDE)=ar(ΔBAE)+ar(ΔAED)=ar(ΔABD)+ar(ΔBDE) ltBrgt⇒ 2ar(ΔBDE)=ar(ΔABD) ...(v)
चूँकि D,BC का मध्य बिंदु है|
∴ ar(ΔABD)=12ar(ΔABC) ...(vi)
(v) तथा (vi ) से,
2ar(ΔBDE)=12ar(ΔABC)
⇒ ar(ΔBDE)=14ar(ΔABC) ...(vii)
(ii)ar(ΔDEF) को (vi ) के दोनों तरफ घटाने पर हमें मिलता है|
ar(ΔBDE)−ar(ΔDEF)=ar(ΔAED)−ar(ΔDEF)
⇒ ar(ΔBEF)=ar(ΔDEF)
(iii ) ,(i ) तथा (vii ) से,
ar(ΔBCE)=2ar(ΔBDE)
=12ar(ΔABC)
चूँकि D का मध्य बिंदु है तथा BC,AD⊥BC पाइथागोरस प्रमेय से
AD2=AB2−BD2
=AB2−(12AB)2=AB2−14AB2
अब ar(ΔAFD)=12(FD)(AD)=√34(FD)(AB) ...(viii)
उसी तरह ar(ΔEFD)=√34(FD)(BE)=√34(FD)(12AB)
=√34ar(ΔAFD) ...(viii) से,
=12ar(ΔBFE) [(viii) से ]...(ix )
⇒ ar(ΔBFE)=2ar(ΔFED)
(iv)ar(ΔBFE)+ar(ΔFED)=3ar(ΔFED)
⇒ ar(ΔBED)=3ar(ΔFED) ...(x)
(v) पुनः ar(ΔAFC)=ar(ΔAFD)+ar(ΔADC)
=ar(ΔBEF)+2ar(ΔBED)
=2ar(ΔFED)+6ar(ΔFED) ...[(x)]
=8ar(ΔFED)
⇒ ar(ΔBED)=18ar(ΔAFC)
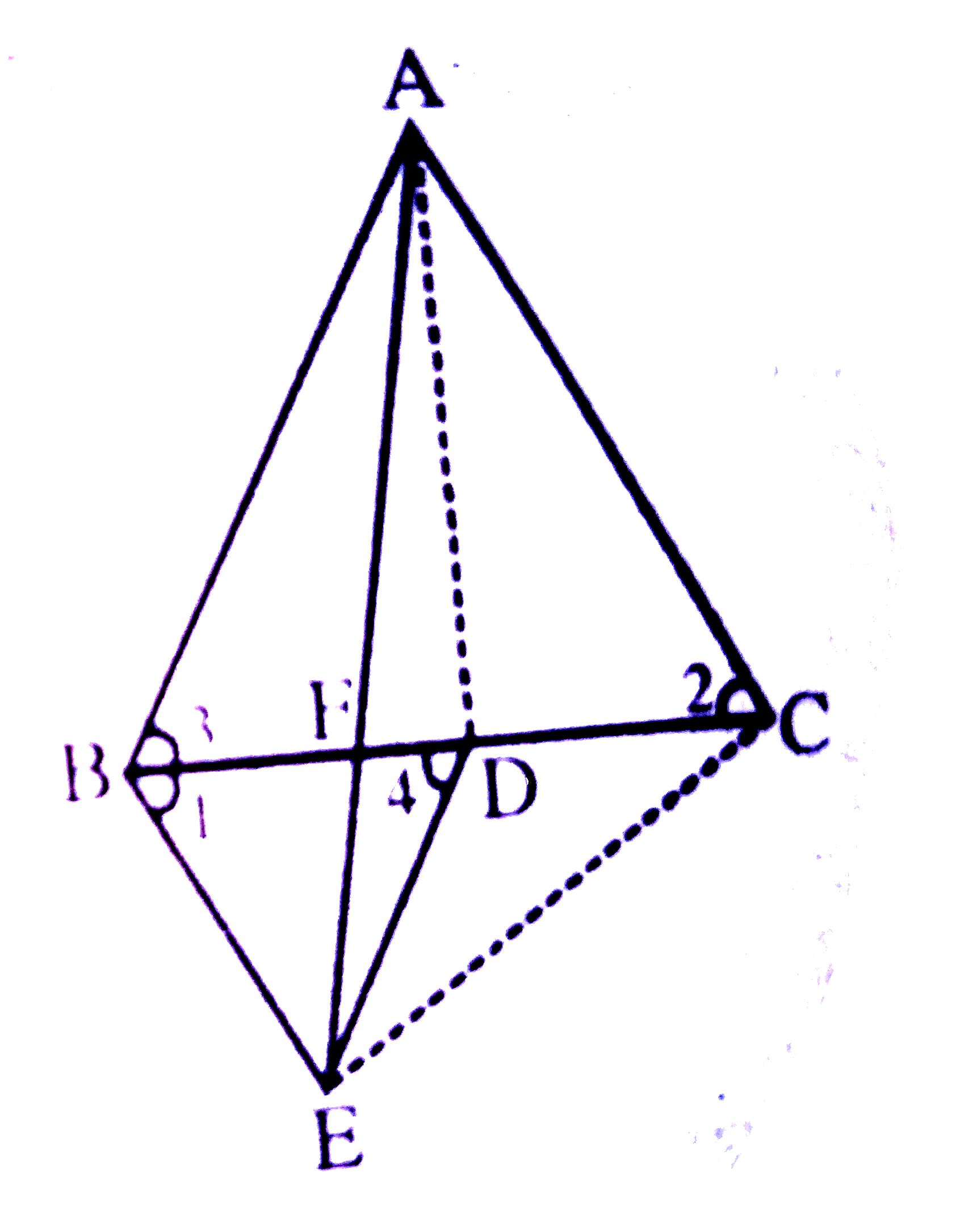
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 11.1
24 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - वस्तुनिष्ट प्रश्न
7 Videos
- समांतर चतुर्भुजBOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - वस्तुनिष्ठ प्रश्न
9 Videos
- हीरोन का सूत्र BOOK - KC SINHACHAPTER - हीरोन का सूत्र EXERCISE - वस्तुनिष्ठ प्रश्न
13 Videos
Similar Questions
रिक्त स्थान को भरें :
(i) सर्वांगसम आयतों के क्षेत्रफल ...........होते है|
(ii) किसी समचतुर्भुज का क्षेत्रफल उसके विकर्णों की लम्बाइयों के गुणनफल का .....होता है
(iii) समलम्ब का क्षेत्रफल उसके समांतर भुजाओं के बीच की दुरी तथा समांतर भुजाओं के योग के गुणनफल का ......होता है|
(iv) सर्वांगसम त्रिभुजों के क्षेत्रफल ........होते है|
(v) एक ही आधार तथा एक ही समांतर रेखाओं के मध्य बने त्रिभुज क्षेत्रफल में ...........होते है|
View Solutionसमचतुर्भुज के विकर्णों का गुणनफल समचतुर्भुज के क्षेत्रफल का कितना गुना होता है ?
View Solutionचतुर्भुज के चारों कोणों का योग कितना समकोण होता है?
View Solutionयदि किसी ΔABC में BC=a,CA=b AB=c हो तो ΔABC की अर्धपरिमिति है
View SolutionIf ABCD is a parallelogram, the prove that ar(ABD)=ar(BCD)=ar(ABC)=ar(ACD)=1/2a r(∣∣gmA B C D)
View SolutionIn the figure, ABC and BDE are two equilateral triangle such that D is the mid-point of BC. If AE intersects BC at F, show that:
(i) ar(ΔBDE)=14ar(ΔABC) (ii) ar(ΔBDE)=12ar(ΔBAE)
(iii) ar(ΔABC)=2ar(ΔBEC) (iv) ar(ΔBFE)=ar(ΔAFD)
(v) ar(ΔBFE)=2ar(ΔFED) (vi) ar(ΔFED)=18ar(ΔAFC)

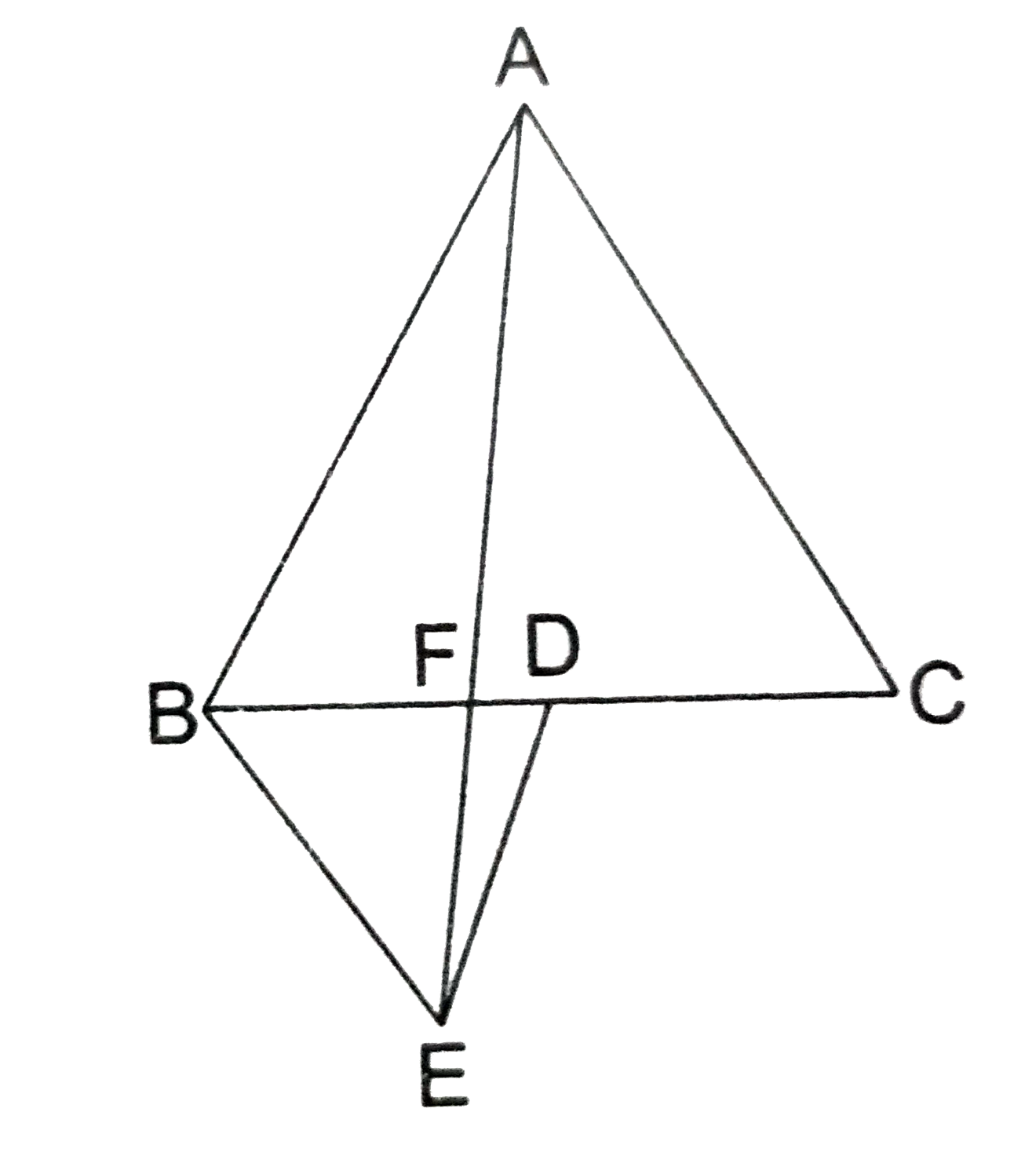
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).
View Solutionसत्य/असत्य बताइए तथा उत्तर का औचित्य भी बताइए -
ABC और BDE दो समबाहु त्रिभुज इस प्रकार है की D भुजा BC का मध्य-बिंदु है। तब
ar(BDE)=14ar(ABC).
View SolutionIn the following figure , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that
(i) ar (BDE) = 14 ar (ABC)
(ii) ar (BDE) = 12 ar (BAE)
(iii) ar (ABC)= 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 18 ar(AFC)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=14ar(ΔABC).
View SolutionIn fig, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that: (i) ar(BDE)= 1/4 ar(ABC) (ii) ar(BDE)= 1/2 ar(BAE)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE)=14 ar(ABC).
View SolutionIn triangle ABC ,P is a point on BC such that BP : PC = 1 : 2 and Q is the mid point of BP. then, ar(triangle ABQ) :ar (triangle ABC) is equal to: त्रिभुज ABC में, P, BC पर स्थित ऐसा बिंदु है कि BP : PC = 1 : 2 है और Q, BP का मध्य बिंदु है | तो ar(triangle ABQ) :ar (triangle ABC) का मान क्या होगा ?
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 3 : 4 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 3 : 4 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान ज्ञात करें |
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 4 : 3 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ACB) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 4 : 3 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ACB) का मान ज्ञात करें |
View Solution
