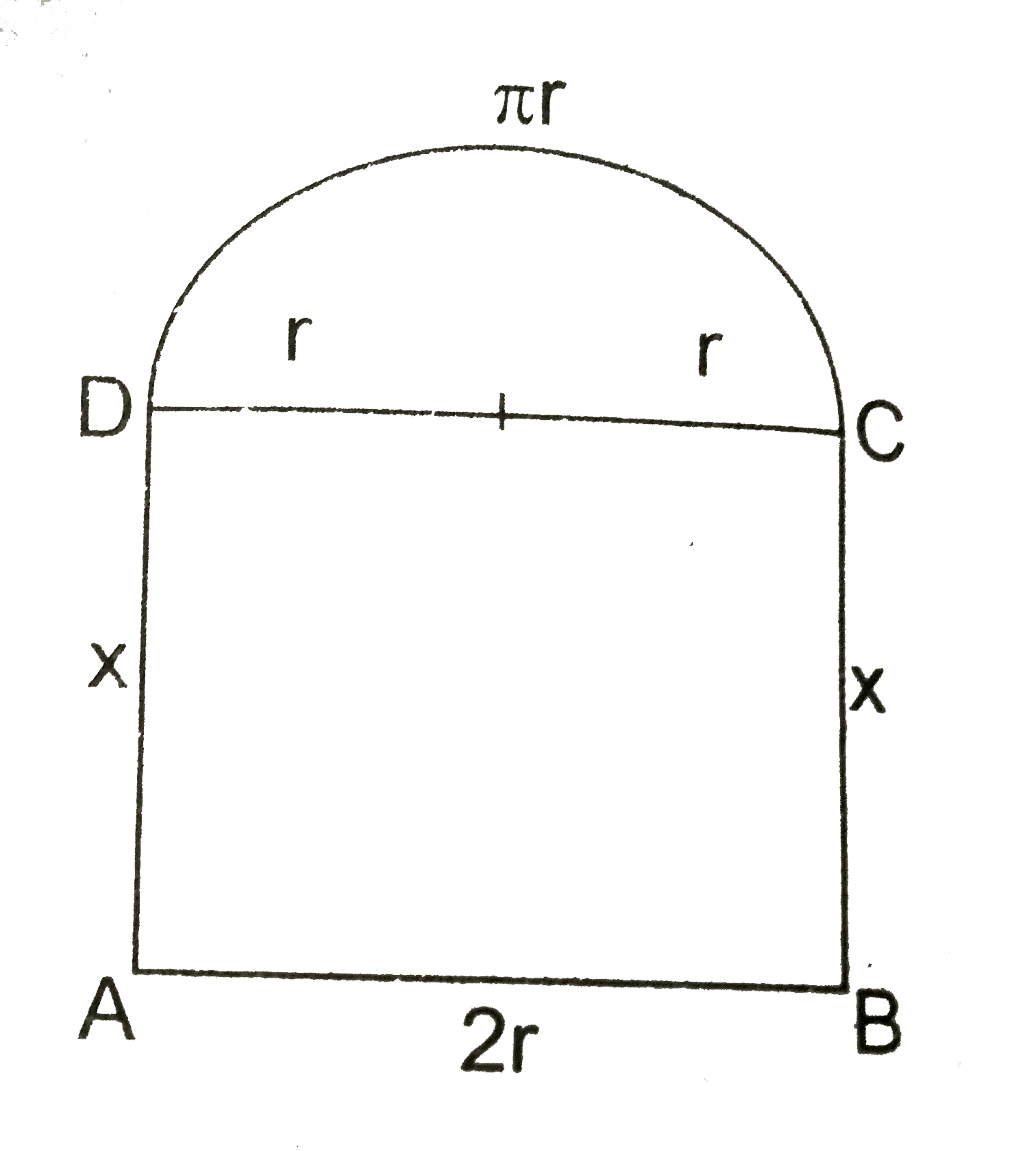
किसी आयत के ऊपर से बने अर्धवृत के आकार वाली खिड़की है। खिड़की का सम्पूर्ण परिमाप 10 मी है। पूर्णतया खुली खिड़की से अधिकतम प्रकाश आने के लीएखिड़की की विमाएँ ज्ञात कीजिए।
माना अर्धवृत्त की त्रिज्या =r
∴P= परिमाप = 10 (दिया है)
⇒2x+2r+12(2πr)=10
implies2x=10-r(pi+2)" "।।।(1)
पुनः माना A खिड़की का क्षेत्रफल है
∴A= अर्धवृत्त का क्षेत्रफल + आयत का क्षेत्रफल
=12πr2+2rx
⇒A=12πr2+r[10−r(π+2)] [समीकरण (1 ) से]
=12πr2+10r−r2π−2r2
=10r−πr22−2r2
⇒dAdr=10−πr−4r ।।।(2)
और d2Adr2=−π−4 ।।।(3)
उच्चतम और निम्नतम मान के लीए dAdr=0
⇒10−πr−4r=0⇒10=(4+π)r
⇒r=104+π
समीकरण (3 ) में r=104+π रखने पर, d2Adr2<0
∴r=104+π पर A का स्थानीय मान उच्चतम होगा।
∴ अर्धवृत्त की त्रिज्या r=104+π ।।।(4)
और आयत की एक भुजा =2r=2×104+π=204+π
समीकरण (1 ) द्वारा आयत की दूसरी भुजा
x=12[10−r(π−2)]
=12[10−(10π+4)(π+2)] [समीकरण (4 ) से]
=202(π+4)=10π+4
∴खिड़की से आने वाला प्रकाश उच्चतम होगा जब क्षेत्रफल उच्चतम है। इसलिए, खिड़की की विमाएँ निम्न है
त्रिज्या =r=10π+4, लम्बाई =2r=20π+4, चौड़ाई =x=10π+4
Topper's Solved these Questions
- अवकलन के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6A
20 Videos
- अवकलन के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6B
15 Videos
- अवकलन के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6.5
48 Videos
- अवकल समीकरण BOOK - NOOTAN HINDICHAPTER - अवकल समीकरण EXERCISE - विविध प्रश्नावली
18 Videos
- आव्यूह BOOK - NOOTAN HINDICHAPTER - आव्यूह EXERCISE - विविध प्रश्नावली
15 Videos
Similar Questions
व्रत के क्षेत्रफल की परिवर्तन की दर, इसकी त्रिज्या r की सापेक्ष ज्ञात कीजिए जबकि r=3.5 सेमी है.
View Solutionसिद्ध कीजिए की फलन f(x)=3x+2,R पर एक निरन्तर वृद्धिमान फलन है.
View Solutionदिए गए फलानो के उच्चतम या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
(i) f(x)=(2x−1)2+3
View Solutionनिम्नलिखित अवकल समीकरणों में से प्रत्येक की कोटि एवं घात (यदि परिभाषित हो) ज्ञात कीजिए।
(i) d2ydx2+5x(dydx)2−6y=logx
(ii) (dydx)3−4(dydx)2+7y=sinx
(iii) d4ydx4−sin(d3ydx3)=0
View Solutionमान लीजिए कि A=[0101] हो तो दिखाइए कि सभी n∈N के लिए (al+bA)n=anI+nan−1bA, जहाँ I कोटि 2 का तत्समक आव्यूह है ।
View Solutionकिसी वर्ग के विपरीत शीर्षो के निर्देशांक (1,2) तथा (3,8) है , तो शीर्ष (1,2) से होकर जाने वाली रेखाओ तथा विकर्ण का समीकरण ज्ञात कीजिए ।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए की किसी विषम पदों वाली समांतर श्रेढ़ी का योगफल श्रेढ़ी में माढ्य पद और पदों की संख्या के गुणगंफल के बराबर होता है |
View Solutionकिसी त्रिभुज एब्स के शीर्ष A(−3,4),B(6,−2) और C(2,5) है। बिन्दु A से होकर जाने वाली माध्यिका का समीकरण ज्ञात कीजिए ।
View Solutionकिसी कारखाने में बने एक बल्ब कि 150 दिनों के उपयोग के बाद फ्यूज होने कि प्रायिकता 0 .05 है प्रायिकता ज्ञात कीजिए कि इस प्रकार के 5 बल्बों में से - एक से अधिक
View Solutionएक पत्थर क्षैतिज से 30∘ का कोण बनाते हुए 100 मी./से. के वेग से फेंकी जाती है। ज्ञात कीजिए -
(i)पत्थर द्वारा प्राप्त की गई अधिकतम ऊँचाई
(ii) अधिकतम ऊँचाई प्राप्त करने के लिए इसके द्वारा लिया गया समय। (g=10मी./से.)2
View Solutionबस की खिड़की से न झाँकें। (भाववाच्य में बदलिए)
View Solutionहीरोन के सूत्र के प्रयोग से किसी त्रिभुज का क्षेत्रफल ज्ञात करना
View SolutionThe area of a regular hexagon is equal to the area of the square. What is the ratio of the perimeter of the regular hexagon to the perimeter of square? सम षटभुज का क्षेत्रफल वर्ग के क्षेत्रफल के बराबर है। सम षटभुज के परिमाप का वर्ग के परिमाप से क्या अनुपात है?
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View SolutionThe perimeter and length of a rectangle are in the ratio of 8:1, and the area of the rectangle is 1323cm2. Find the length of the rectangle.
एक आयत का परिमाप और उसकी लंबाई 8:1 के अनुपात में है। आयत का क्षेत्रफल 1323 वर्ग सेमी है। आयत की लंबाई ज्ञात कीजिए।
View Solution
