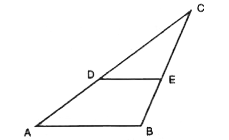
चित्र में AD तथा AE क्रमशः BC तथा AC पर लम्ब है, तो दर्शाइए की:
(i)ΔADC~ΔBEC
(ii)CA×CE=CB×CD
(iii)ΔABC~ΔDEC
(iv)CD×AB=CA×DE
Δ'sADC तथा BEC में
∠ADC=∠BEC=90∘ (दिया है)
∠ACD=∠BCE [उभयनिष्ट]
अतः समरूपता की AA कसौटी से
ΔADC~ΔBEC
(ii) दिया है
ΔADC~ΔBEC [जैसा की ऊपर सिद्ध किया है]
⇒ ACBC=DCEC
⇒ CA×CE=CB×CD
(iii)Δ'sABC और DECमें
ACBC=DCEC
⇒ ACDC=BCEC
साथ ही ∠ACB=∠DCE
अतः समरूपता की SAS कसौटी से
ΔABC~ΔDEC
(iv ) दिया है
ΔABC~ΔDEC [जैसा की ऊपर सिद्ध किया है]
⇒ ABDE=ACDC
⇒ AB×DC=AC×DE
⇒ CD×AB=CA×DE
Topper's Solved these Questions
- त्रिभुजेंBOOK - RD SHARMACHAPTER - त्रिभुजेंEXERCISE - प्रश्नावली 4.1
12 Videos
- त्रिभुजेंBOOK - RD SHARMACHAPTER - त्रिभुजेंEXERCISE - प्रश्नावली 4.2
20 Videos
- त्रिकोणमितीय सर्वसमिकाएँ BOOK - RD SHARMACHAPTER - त्रिकोणमितीय सर्वसमिकाएँ EXERCISE - बहु विकल्पीय प्रश्न
28 Videos
- दो चार वाले रैखिक समीकरण युग्म BOOK - RD SHARMACHAPTER - दो चार वाले रैखिक समीकरण युग्म EXERCISE - बहु विकल्पीय प्रश्न
16 Videos
Similar Questions
कोष्ठक में दिए हुए शब्दों में से ही शब्दों को चुनकर रिक्त स्थान को भारिये:
सभी वृत.......(सर्वांगसम, समरूप) होते है|
View Solutionत्रिभुज ABC की भुजाओं AB और AC बिंदु D और E इस प्रकार है की DE भुजा BC के समानांतर है| यदि|||
AD=6 सेमि , DB = 9 सेमि तथा AE =8 सेमि, हो तो AC ज्ञात करो|
View Solutionयदि secθ+tanθ=x हो तो secθ=
View Solutionनिम्न समीकरण युग्म का अद्वितीय हल होंगे, यदि
kx−y=2
6x−2y=3
View SolutionABC is a triangle in which AB=AC and D is a point on AC such that BC^(2)=AC xx CD .Prove that BD=BC .
View Solution△ABC is an obtuse triangle; obtuse-angled at B. If AD⊥CB ; prove that (AC)2=(AB)2+(BC)2+2BC.BD
View Solutionएक △ABC में, AB = AC तथा D, AC का मध्य बिंदु है और BC2=AC×CD हो तो सिद्ध कीजिए कि BD = BC
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionABC is a triangle with AB= AC and D is a point on AC such that BC2=AC×CD. Prove that BD= BC.
View SolutionΔABC में भुजा BC का मध्य- बिंदु D है, यद्यपि ∠ADC=∠BAC तो सिद्ध कीजिए कि CACD=CBCA
View Solutionदिए गए त्रिभुज ΔABC में दिया है कि DE ∣∣ AB तो निम्नलिखित को ज्ञात कीजिए :
(i) ACCD (ii) CDAD
(iii) ADAC (iv) CEBC (v) CDCE (vi) BCAC
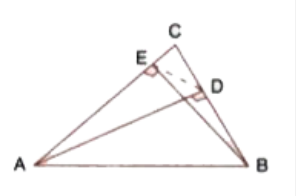
View SolutionThe following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively. Show that :
CA×CE=CB×CD

View SolutionThe following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively. Show that :
CD×AB=CA×DE
View SolutionIn a triangle ABC, AB =AC and the perimeter of A ABC is 8(2 + sqrt 2) cm . If the length of BC is sqrt 2 times the length of AB, then find the area of triangle ABC . एक त्रिभुज ABC में AB = AC और triangle ABC की परिधि 8(2 + sqrt 2) सेमी है। यदि 80 की लंबाई AB की लंबाई से sqrt 2 गुना है, तो triangle ABC का क्षेत्रफल ज्ञात कीजिए|
View SolutionIn triangle ACE , B and D are the points on side AC and CE , respectively, such that BD is parallel to AE and AE = (8/3)BD. What is the ratio of the area of triangle BDC to that of triangle AEC . triangle ACE में, B और D वे बिंदु है जो क्रमशः भुजा AC और CE पर इस प्रकार स्थित है कि BD, AE के समानांतर है तथा AE = (8/3)BD है | triangle BDC तथा triangle AEC के क्षेत्रफल में अनुपात ज्ञात करें |
View SolutionIn triangle ABC , AD bisects angle A and intersects BC at D. If BC = a ,AC = b and AB = c, then BD = ? त्रिभुज ABC में, AD कोण A को समद्विभाजित करता है तथा BC को D पर काटता है | यदि BC = a, AC = b और AB = c है, तो BD = ?
View Solution
