Let △ABC and △ABD be on the same base AB and between
the same parallels AB and CD.
Then the relation between areas of △ABC and △ABD will be:
मान लीजिये कि △ABC तथा△ABD एक ही आधार AB पर स्थित हैं तथा समान समानांतर रेखाओं AB तथा CD के बीच हैं| △ABC तथा△ABD के क्षेत्रफलों में क्या संबंध होगा ?
Area (△ABC)= 12 Area (△ABD)
Area (△ABC)= Area (△ABD)
Area (△ABD)= 13 Area (△ABC)
Area (△ABD)= 12 Area (△ABC)
To determine the relationship between the areas of triangles ABC and ABD, we can follow these steps:
1. Identify the Base and Height:
Both triangles ABC and ABD share the same base AB. Let's denote the height of triangle ABC from point C to line AB as H1 and the height of triangle ABD from point D to line AB as H2.
2. Area Formula for Triangles:
The area of a triangle is given by the formula:
Area=12×Base×Height
Therefore, for triangle ABC, the area AABC can be expressed as:
AABC=12×AB×H1
And for triangle ABD, the area AABD can be expressed as:
AABD=12×AB×H2
3. Comparing the Areas:
Since both triangles share the same base AB, we can compare their areas directly:
AABDAABC=12×AB×H212×AB×H1
The 12 and AB cancel out, leading to:
AABDAABC=H2H1
4. Conclusion:
Since the triangles are situated between the same parallel lines AB and CD, the heights H1 and H2 can be considered equal if points C and D are at the same vertical distance from line AB. Therefore, we conclude:
AABD=AABC
This means that the areas of triangle ABC and triangle ABD are equal.
Final Answer:
The area of triangle ABC is equal to the area of triangle ABD.
Both triangles ABC and ABD share the same base AB. Let's denote the height of triangle ABC from point C to line AB as H1 and the height of triangle ABD from point D to line AB as H2.
The area of a triangle is given by the formula:
Area=12×Base×Height
Therefore, for triangle ABC, the area AABC can be expressed as:
AABC=12×AB×H1
And for triangle ABD, the area AABD can be expressed as:
AABD=12×AB×H2
Since both triangles share the same base AB, we can compare their areas directly:
AABDAABC=12×AB×H212×AB×H1
The 12 and AB cancel out, leading to:
AABDAABC=H2H1
Since the triangles are situated between the same parallel lines AB and CD, the heights H1 and H2 can be considered equal if points C and D are at the same vertical distance from line AB. Therefore, we conclude:
AABD=AABC
This means that the areas of triangle ABC and triangle ABD are equal.
The area of triangle ABC is equal to the area of triangle ABD.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The triangle is formed by joining the mid-points of the sides AB,BC and CA of △ABCand the area of △PQR is 6cm2, then the area of △ABC is :
A36cm2B12cm2C18cm2D24cm2
In △ABC , the medians AD, BE and CF meet at O. What is the ratio of the area of △ABD to the area of △AOE ?
View SolutionIn a triangle ABC, having AD is median and area of triangle ABD= 120m2. Find area of triangle ABC.
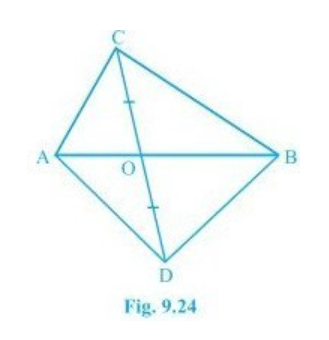
View SolutionIn Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that ar(△ABC)=ar(△ABD)
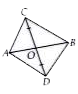
View SolutionIn Figure, ABC and DBC are two triangles on the same base BC such that AB=AC and DB=DC. Prove that ∠ABD=∠ACD
View SolutionIn Fig. 9.29 ratio of the area of triangle ABC to the area of triangle ACD is the same as the ratio of base BC of triangle ABC to the base CD of triangle ACD.

View SolutionIn figure, ABC and ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O , show that ar(△ABC)=ar(△ABD).
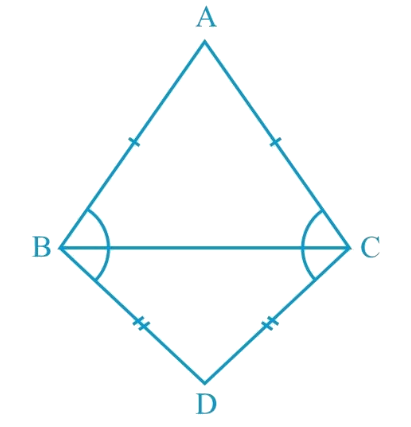
View SolutionIn Figure, ABC and DBC are two isosceles triangles on the same base BC such that AB=AC and DB=CD. Prove that ∠ABD= ∠ACD
View Solution