मैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
चारो समीकरणों में कोनसी समीकरण यह प्रदर्शित करती हो की स्थिर विधुत क्षेत्र की रेखाएं बंद लूप नहीं बनाती ?
सेमीकरण (iii ) यदि →E समय पर निर्भर नहीं हो
∮→E,d→l=0
Topper's Solved these Questions
- विद्युत -चुम्बकीय तरंगे , संचार एवं समकालीन भौतिकी BOOK - SCIENCE PUBLICATIONCHAPTER - विद्युत -चुम्बकीय तरंगे , संचार एवं समकालीन भौतिकी EXERCISE - अन्य महत्वपूर्ण प्रश्न ( आंकिक प्रश्न )
5 Videos
- विद्युत -चुम्बकीय तरंगे , संचार एवं समकालीन भौतिकी BOOK - SCIENCE PUBLICATIONCHAPTER - विद्युत -चुम्बकीय तरंगे , संचार एवं समकालीन भौतिकी EXERCISE - अन्य महत्वपूर्ण प्रश्न ( वस्तुनिष्ट प्रश्न )
20 Videos
- प्रत्यावर्ती धारा BOOK - SCIENCE PUBLICATIONCHAPTER - प्रत्यावर्ती धारा EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न)
10 Videos
- विद्युत क्षेत्र BOOK - SCIENCE PUBLICATIONCHAPTER - विद्युत क्षेत्र EXERCISE - अन्य महत्वपूर्ण प्रश्न (आंकिक प्रश्न )
4 Videos
Similar Questions
एक भू - केंद्र अभिग्राही (a ) 5 MHz तथा (b ) 100 MHz के संकेत ग्रहण कर रहा है जिन्हे 300 m ऊंचाई पर स्थित्त भू - प्रेषित्र से संप्रेषित किया जा रहा है दोनों के बीच 100 km दुरी है पता लगाइए की संकेत अंतरिक्ष तरंगो के रूप में व्योम तरंग से या उपग्रह ट्रांसपोंडर ( प्रेषानुकर ) से प्राप्त किए जा रहे है पृथ्वी की त्रिज्या ≈6.4×106m आयनमंडल का mmax =1012m3 ।
View Solutionविधुत चुम्बकीय तरंगो की प्रकृति होती है -
View Solutionएक 50Ω का प्रतिरोध 200V,60Hz आपूर्ति से संयोजित है।
परिपथ में धारा का rms मान कितना है ?
View Solutionदो समान आवेश d दूरी पर स्थित हैं एक तीसरे आवेश को लम्बार्धक पर x दूरी पर रखा गया है। यह आवेश अधिकतम कृलॉम बल का अनुभव करें तब x का मान क्या होगा?
View SolutionA vector →A points vertically upward and →B oints towards north. The vector product →A×→B is
View SolutionConsider Gauss's law
∮→E⋅→ds=qε0
Then, for the situation shown in figure at the Gaussian surface
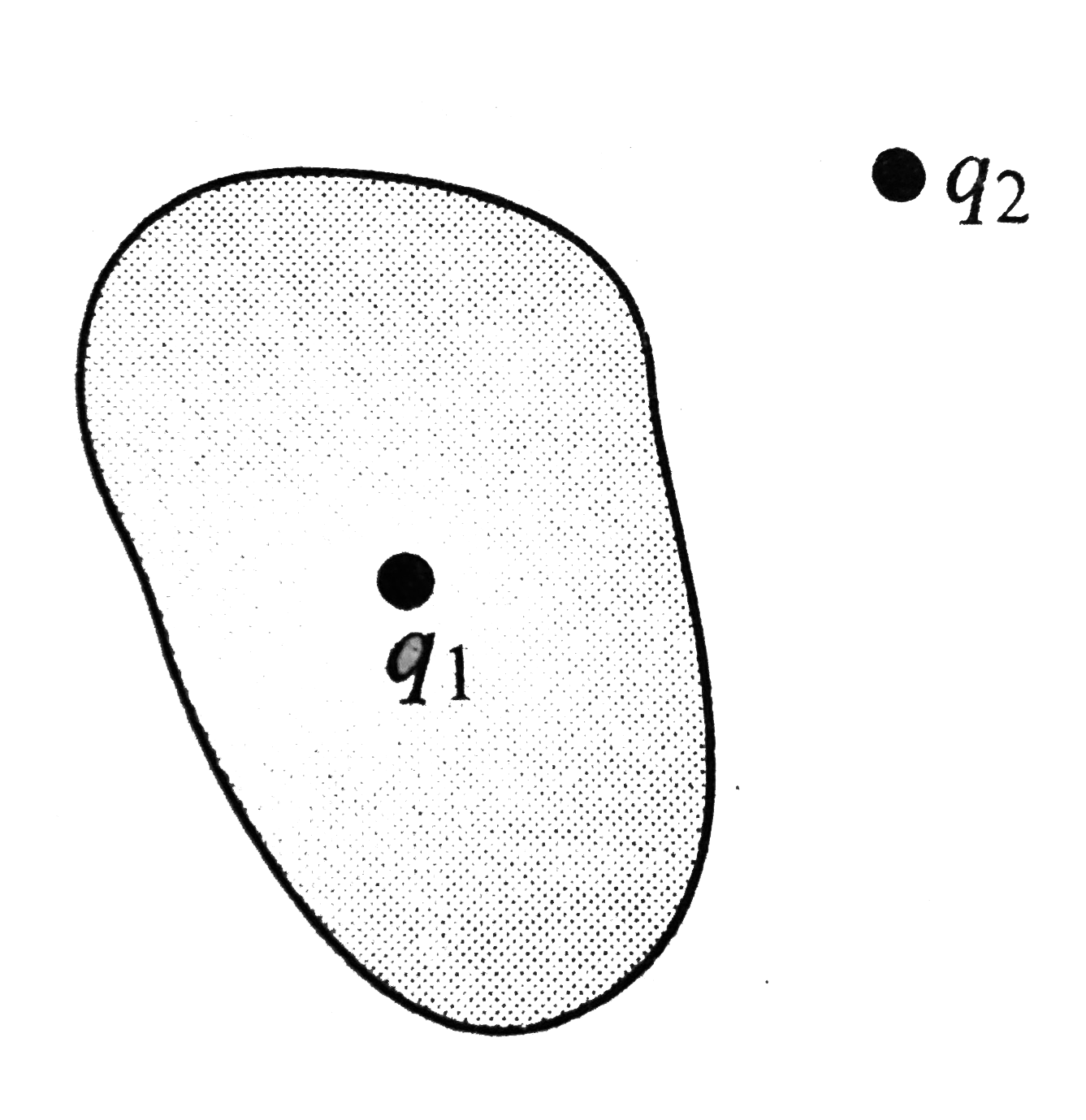
View SolutionMaxwell's equation ∮→B⋅d→s=0 says
View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
कौन - कौन से समीकरणों →E ओर →B के स्त्रोत प्रदर्शित करती है ओर कौन सी नहीं ? आवेश रहित होने की स्थिति में समीकरणों का क्या प्रारूप होगा ।
View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
कौन - कौन से समीकरणों →E ओर →B के स्त्रोत प्रदर्शित करती है ओर कौन सी नहीं ? आवेश रहित होने की स्थिति में समीकरणों का क्या प्रारूप होगा ।
View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
स्थिर विधुत व चुम्बकीय क्षत्रो के लिए मैक्सवेल सेमीकरणे लिखिये
View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
यदि चुम्बक का एक धुव होता तो कौन सी समीकरणों को परिवर्तित करना पड़ता
View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
चारो समीकरणों में कौन सी समीकरण यह प्रदर्शित करती है की चुम्बकीय क्षेत्र किसी से उत्सर्जित अथवा समाप्त किया जा सकता है
View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
क्या उपरोक्त सेमीकरणे विभिन्न माध्यमों , परावैधुत , चालक व प्लाज्मा इत्यादि के लिए सही है।
View SolutionThe maxwells four equations are written as i. oint vec(E).vec(dS) = (q)/(epsilon_(0)) ii. oint vec(B).vec(dS) = 0 iii. oint vec(E ).vec(dl) = (d)/(dt) oint vec(B).vec(dS) iv. oint vec(B).vec(dl) = mu_(0) epsilon (d)/(dt) oint vec(E).vec(dS) The equations which have sources of vec(E ) and vec(B) are
View SolutionAssertion: Two charged metallic surfaces parallel to each other always carry equal and opposite charges.
Reason: Gauss's law: ∮→E⋅d→S=qInε0
View Solution
