मैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
यदि चुम्बक का एक धुव होता तो कौन सी समीकरणों को परिवर्तित करना पड़ता
समीकरण (ii ) व (iii ) में परिवर्तन करना होगा समीकरण (ii ) इस तथ्य पर आधारित है की अकेले ध्रुव का आस्तित्व नहीं है यदि अकेला ध्रुव है तो समीकरण के दाहिने पक्ष में पद qm चुम्बकीय ध्रुव की सामर्थ्य भी होगा जो ग्रास के नियम के तुल्य होगा तब -
∮→B,d→A−qm× नियताक
इसी प्रकार (iii ) समीकरण
∮→E।d→l=Im× नियतांक −ddt∫S→Bd→A
Topper's Solved these Questions
- BOOK - SCIENCE PUBLICATIONCHAPTER - विद्युत -चुम्बकीय तरंगे , संचार एवं समकालीन भौतिकी EXERCISE - अन्य महत्वपूर्ण प्रश्न ( आंकिक प्रश्न )5videos
विद्युत -चुम्बकीय तरंगे , संचार एवं समकालीन भौतिकी
- BOOK - SCIENCE PUBLICATIONCHAPTER - विद्युत -चुम्बकीय तरंगे , संचार एवं समकालीन भौतिकी EXERCISE - अन्य महत्वपूर्ण प्रश्न ( वस्तुनिष्ट प्रश्न )20videos
विद्युत -चुम्बकीय तरंगे , संचार एवं समकालीन भौतिकी
- BOOK - SCIENCE PUBLICATIONCHAPTER - प्रत्यावर्ती धारा EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न)10videos
प्रत्यावर्ती धारा
- BOOK - SCIENCE PUBLICATIONCHAPTER - विद्युत क्षेत्र EXERCISE - अन्य महत्वपूर्ण प्रश्न (आंकिक प्रश्न )4videos
विद्युत क्षेत्र
Similar Questions
एक भू - केंद्र अभिग्राही (a ) 5 MHz तथा (b ) 100 MHz के संकेत ग्रहण कर रहा है जिन्हे 300 m ऊंचाई पर स्थित्त भू - प्रेषित्र से संप्रेषित किया जा रहा है दोनों के बीच 100 km दुरी है पता लगाइए की संकेत अंतरिक्ष तरंगो के रूप में व्योम तरंग से या उपग्रह ट्रांसपोंडर ( प्रेषानुकर ) से प्राप्त किए जा रहे है पृथ्वी की त्रिज्या ≈6.4×106m आयनमंडल का mmax =1012m3 ।
02:20View Solutionविधुत चुम्बकीय तरंगो की प्रकृति होती है -
01:52View Solutionएक 50Ω का प्रतिरोध 200V,60Hz आपूर्ति से संयोजित है।
परिपथ में धारा का rms मान कितना है ?02:06View Solutionदो समान आवेश d दूरी पर स्थित हैं एक तीसरे आवेश को लम्बार्धक पर x दूरी पर रखा गया है। यह आवेश अधिकतम कृलॉम बल का अनुभव करें तब x का मान क्या होगा?
05:40View SolutionA vector →A points vertically upward and →B oints towards north. The vector product →A×→B is
05:40View SolutionConsider Gauss's law
∮→E⋅→ds=qε0
Then, for the situation shown in figure at the Gaussian surface
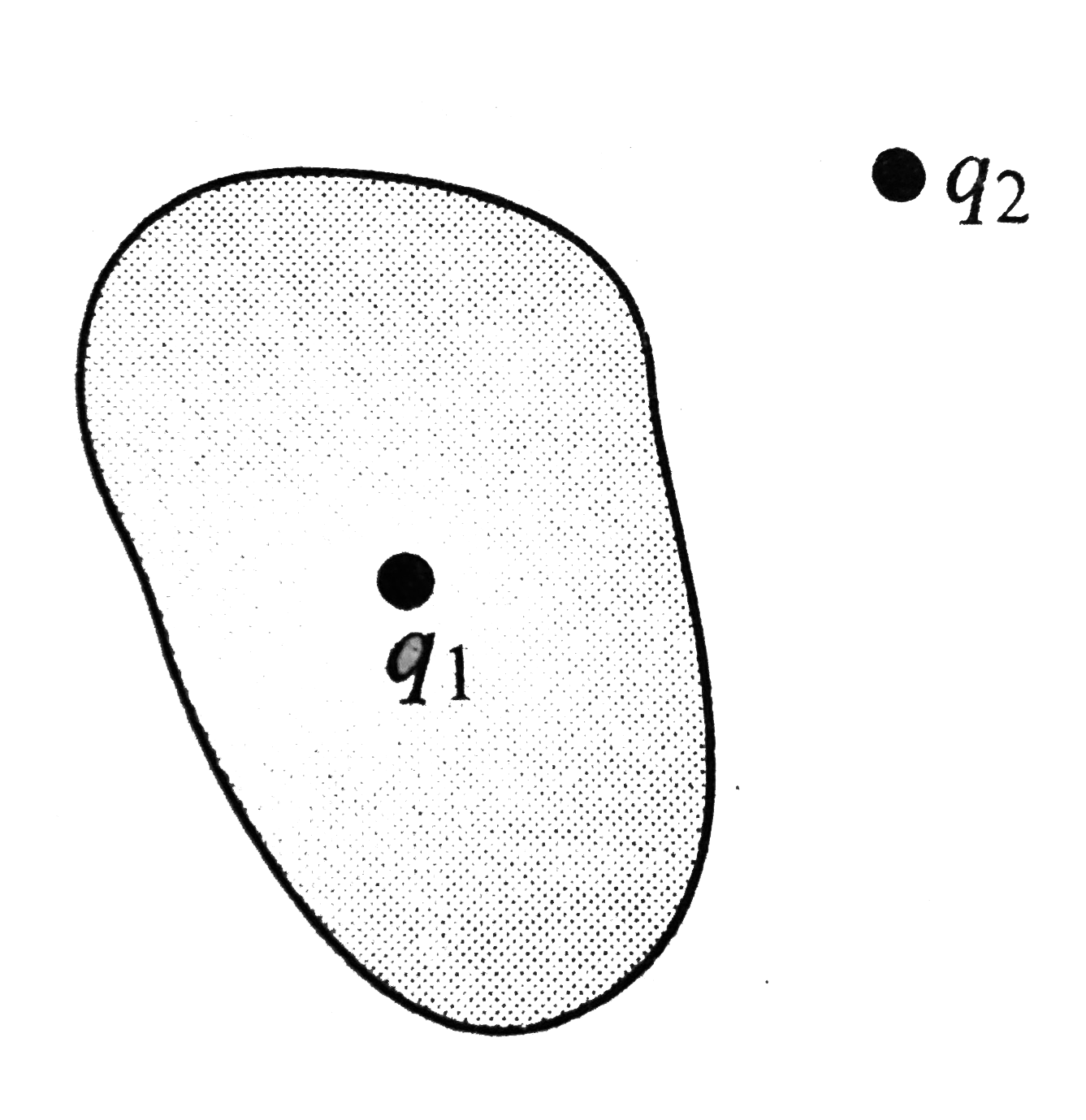 07:54View Solution
07:54View SolutionMaxwell's equation ∮→B⋅d→s=0 says
06:49View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
कौन - कौन से समीकरणों →E ओर →B के स्त्रोत प्रदर्शित करती है ओर कौन सी नहीं ? आवेश रहित होने की स्थिति में समीकरणों का क्या प्रारूप होगा ।07:37View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
कौन - कौन से समीकरणों →E ओर →B के स्त्रोत प्रदर्शित करती है ओर कौन सी नहीं ? आवेश रहित होने की स्थिति में समीकरणों का क्या प्रारूप होगा ।04:59View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
स्थिर विधुत व चुम्बकीय क्षत्रो के लिए मैक्सवेल सेमीकरणे लिखिये02:32View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
चारो समीकरणों में कौन सी समीकरण यह प्रदर्शित करती है की चुम्बकीय क्षेत्र किसी से उत्सर्जित अथवा समाप्त किया जा सकता हैView Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
चारो समीकरणों में कोनसी समीकरण यह प्रदर्शित करती हो की स्थिर विधुत क्षेत्र की रेखाएं बंद लूप नहीं बनाती ?View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
क्या उपरोक्त सेमीकरणे विभिन्न माध्यमों , परावैधुत , चालक व प्लाज्मा इत्यादि के लिए सही है।01:32View SolutionThe maxwells four equations are written as i. oint vec(E).vec(dS) = (q)/(epsilon_(0)) ii. oint vec(B).vec(dS) = 0 iii. oint vec(E ).vec(dl) = (d)/(dt) oint vec(B).vec(dS) iv. oint vec(B).vec(dl) = mu_(0) epsilon (d)/(dt) oint vec(E).vec(dS) The equations which have sources of vec(E ) and vec(B) are
02:20View SolutionAssertion: Two charged metallic surfaces parallel to each other always carry equal and opposite charges.
Reason: Gauss's law: ∮→E⋅d→S=qInε0View Solution

