मैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
कौन - कौन से समीकरणों →E ओर →B के स्त्रोत प्रदर्शित करती है ओर कौन सी नहीं ? आवेश रहित होने की स्थिति में समीकरणों का क्या प्रारूप होगा ।
(i) विद्युत का गाउस नियम (ii) चुम्बकत्व का गाउस नियम (ii) फैराडे का नियम (iv) मैक्सवेल-ऐम्पियर नियम
Topper's Solved these Questions
- विघुतचुंमबकीय तरगेBook:BALAJI PUBLICATIONChapter:विघुतचुंमबकीय तरगेExercise:दीर्घ उत्तरीय प्रश्न
Explore 10 Videos
- विघुतचुंमबकीय तरगेBook:BALAJI PUBLICATIONChapter:विघुतचुंमबकीय तरगेExercise:आकिक प्रश्न ( हल सहित )
Explore 14 Videos
- विकिरण तथा द्रव्य की द्वैत प्रकृति Book:BALAJI PUBLICATIONChapter:विकिरण तथा द्रव्य की द्वैत प्रकृति Exercise:अतिरिक्त अभ्यास
Explore 18 Videos
- विद्युत धाराBook:BALAJI PUBLICATIONChapter:विद्युत धाराExercise:NCERT पाठ्य-पुस्तक के हल
Explore 28 Videos
Similar Questions
मैक्सवेल की वैद्युतचुम्बकत्व की समीकरण लिखिये। ये समीकरण जिन नियमों को व्यक्त करती हैं उन्हें स्पष्ट कीजिये।
View Solutionवृत्ताकार प्लेट वाले एक समान्तर प्लेट संधारित्र की प्लेट की त्रिज्या R = 5.5 सेमी है। इसकी प्लेटों के बीच विद्युत क्षेत्र 1.50×10(12) वोल्ट/मीटर-सेकण्ड की दर से बदल रहा है।
प्लेटों के बीच विस्थापन धारा तथा प्लेटों के बाहर चालन धारा का मान ज्ञात कीजिये।
View Solution(a) एक निवृत्त नाली तपित कैथोड से उत्सर्जित एलेक्ट्रोनो की उस चल का आंकलन कीजिये वे उत्सर्जरक की तुलना में 500 V के विभवांतर पर रखे हुए एनोड से टकराते है एलेक्ट्रोनो की लघु प्रारंभिक चलो की अपेक्षा क्र दे इलेक्ट्रान का आपेक्षिक आवेश 1.76×1011 कॉलम / किग्र है
(b) संग्राहक विभव 10 MV के लिए इलेक्ट्रान की चल ज्ञात करने की लिए उसी सूत्र का प्रयोग करे जो (a) में काम में लाया गया है क्या आप इस सूत्र को गलत पाते है इस सूत्र को किस प्रकार सुधारा जा सकता है
View Solutionकिसी कार की संचायक बैटरी का विधुत वाहक बल 12V है । यदि बैटरी का आंतरिक प्रतिरोध () हो, तो बैटरी से ली जाने वाली अधिकतम धारा का मान क्या है ?
View SolutionA vector →A points vertically upward and →B oints towards north. The vector product →A×→B is
View SolutionConsider Gauss's law
∮→E⋅→ds=qε0
Then, for the situation shown in figure at the Gaussian surface
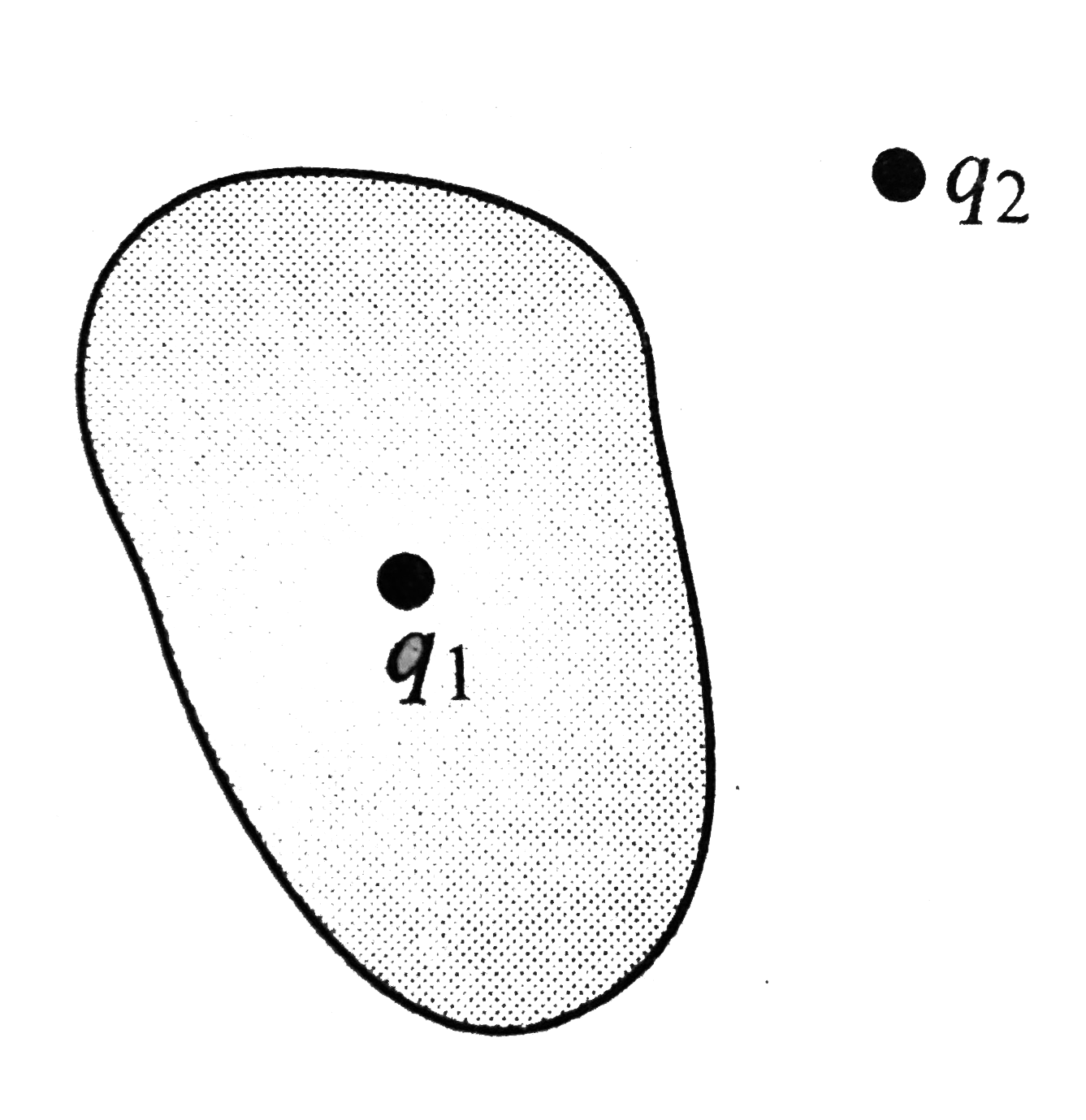
View SolutionMaxwell's equation ∮→B⋅d→s=0 says
View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
कौन - कौन से समीकरणों →E ओर →B के स्त्रोत प्रदर्शित करती है ओर कौन सी नहीं ? आवेश रहित होने की स्थिति में समीकरणों का क्या प्रारूप होगा ।
View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
स्थिर विधुत व चुम्बकीय क्षत्रो के लिए मैक्सवेल सेमीकरणे लिखिये
View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
यदि चुम्बक का एक धुव होता तो कौन सी समीकरणों को परिवर्तित करना पड़ता
View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
चारो समीकरणों में कौन सी समीकरण यह प्रदर्शित करती है की चुम्बकीय क्षेत्र किसी से उत्सर्जित अथवा समाप्त किया जा सकता है
View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
चारो समीकरणों में कोनसी समीकरण यह प्रदर्शित करती हो की स्थिर विधुत क्षेत्र की रेखाएं बंद लूप नहीं बनाती ?
View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
क्या उपरोक्त सेमीकरणे विभिन्न माध्यमों , परावैधुत , चालक व प्लाज्मा इत्यादि के लिए सही है।
View SolutionThe maxwells four equations are written as i. oint vec(E).vec(dS) = (q)/(epsilon_(0)) ii. oint vec(B).vec(dS) = 0 iii. oint vec(E ).vec(dl) = (d)/(dt) oint vec(B).vec(dS) iv. oint vec(B).vec(dl) = mu_(0) epsilon (d)/(dt) oint vec(E).vec(dS) The equations which have sources of vec(E ) and vec(B) are
View SolutionAssertion: Two charged metallic surfaces parallel to each other always carry equal and opposite charges.
Reason: Gauss's law: ∮→E⋅d→S=qInε0
View Solution