Question

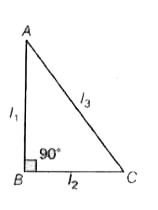
एक त्रिभुजाकार पटल ABC है | AB = 4 सेमी , BC = 3 सेमी तथा $\angle ABC={90}^{\circ }$ | यदि AB, BC तथा CA के परितः जड़त्व आघूर्ण $I_1,I_2$ तथा $I_3$ है, तो निम्न में से कौन - सा कथन सत्य है ?

Options

A. `I_(1)=I_(2)=I_(3)`
B. `I_(2) gt I_(1) gtI_(3)`
C. `I_(3) lt I_(2) lt I_(1)`
D. `I_(3) gt I_(1)gt I_(2)`

Answer

B

Explanation

किसी अक्ष के परितः वस्तु का जड़त्व आघूर्ण के बल द्रव्यमान पर ही निर्भर नहीं करता है अपितु यह घूर्णन अक्ष के परितः द्रव्यमान के वितरण पर भी निर्भर करता है|
चूँकि BC अक्ष के परितः द्रव्यमान वितरण AB तथा CA अक्ष के परितः द्रव्यमान वितरण से अधिक है तथा AB अक्ष के परितः द्रव्यमान वितरण CA अक्ष के परितः द्रव्यमान वितरण से अधिक है| अतः BC अक्ष के परितः घूर्णन त्रिज्या से अधिक होगी तथा AB अक्ष के परितः घूर्णन त्रिज्या CA अक्ष के परितः घूर्णन त्रिज्या से अधिक होगी |
अर्थात `" "k_(BC) gt k_(AB) gt k_(CA)`
`because" "l=mk^(2)`
या `" "l prop k^(2)`
अतः k का मान अधिक होने पर जड़त्व आघूर्ण (l ) का मान भी अधिक होगा अर्थात
`l_(2) gt l_(1) gt l_(3)`