Question

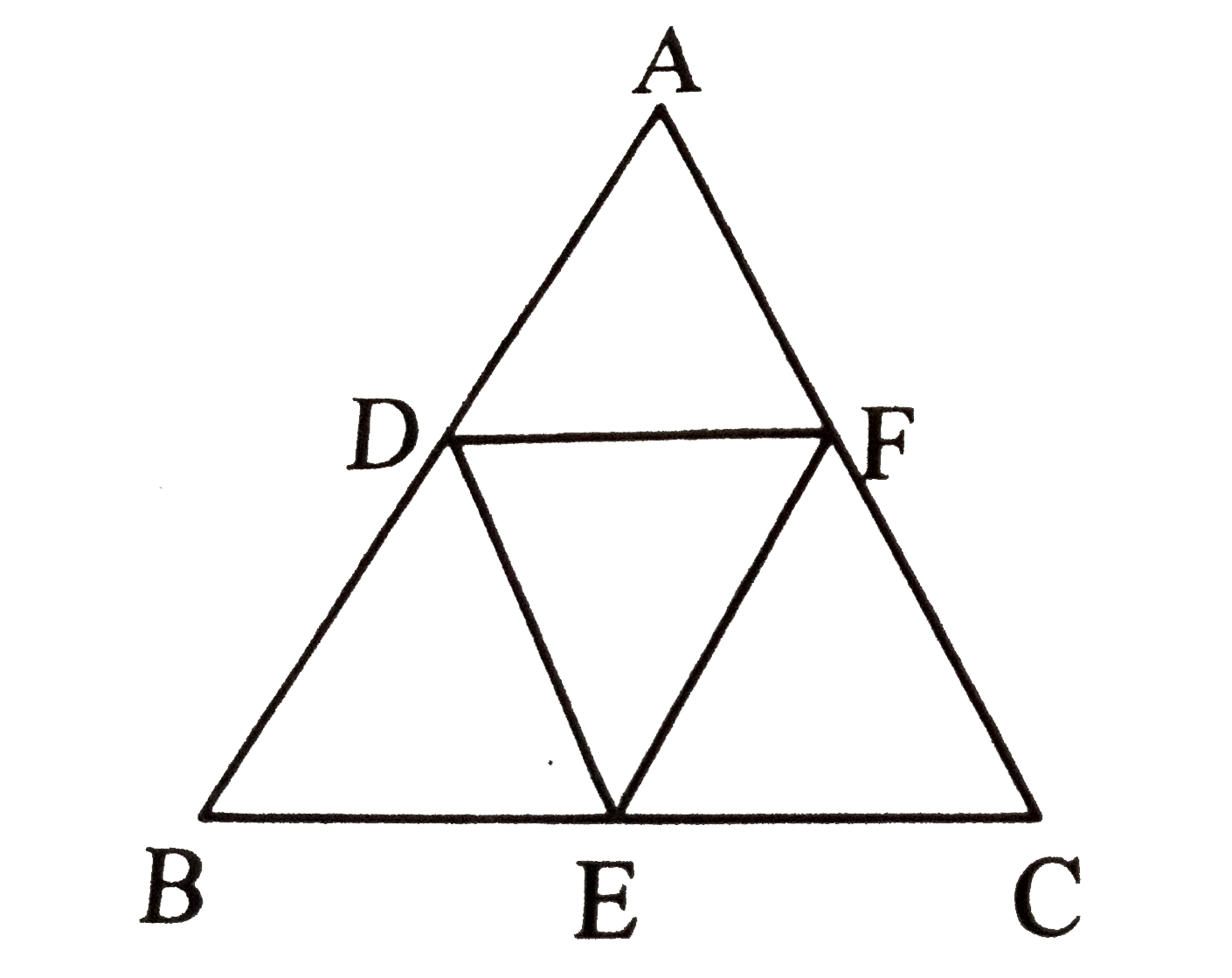
In $△ABC$,D, E and F are the midpoints of sides AB, BC and CA, respectively. If AB = 12 cm, BC = 20 cm and CA = 15 cm, then the value of $\frac{1}{2}(DE+EF+DF)$ is:

त्रिभुज ABC में, D, E तथा F क्रमशः भुजाओं AB, BC तथा CA के मध्य बिंदु हैं | यदि AB =12 सेमी, BC = 20 सेमी तथा CA =15 सेमी है, तो $\frac{1}{2}(DE+EF+DF)$ का मान क्या होगा ?

Options

A. 23.5 cm
B. 11.75 cm
C. 15.67 cm
D. 5.88 cm

Explanation

To solve the problem, we need to find the value of $$\frac{1}{2}(DE+EF+DF)$$ in triangle $$ABC$$ where $$D,E,F$$ are the midpoints of sides $$AB,BC,$$ and $$CA$$ respectively.

1. Identify the lengths of the sides of triangle ABC:
- \( AB = 12 \, \text{cm} \)
- \( BC = 20 \, \text{cm} \)
- \( CA = 15 \, \text{cm} \)

2. Use the property of midpoints:
- The segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length.
- Therefore:
- \( DE \) (midpoint of \( AB \) and \( BC \)) is parallel to \( AC \) and \( DE = \frac{1}{2} AC = \frac{1}{2} \times 15 = 7.5 \, \text{cm} \)
- \( EF \) (midpoint of \( BC \) and \( CA \)) is parallel to \( AB \) and \( EF = \frac{1}{2} AB = \frac{1}{2} \times 12 = 6 \, \text{cm} \)
- \( DF \) (midpoint of \( CA \) and \( AB \)) is parallel to \( BC \) and \( DF = \frac{1}{2} BC = \frac{1}{2} \times 20 = 10 \, \text{cm} \)

3. Calculate the sum of the lengths of segments DE, EF, and DF:
\( DE + EF + DF = 7.5 + 6 + 10 = 23.5 \, \text{cm} \)

4. Calculate \( \frac{1}{2} (DE + EF + DF) \):
\( \frac{1}{2} (DE + EF + DF) = \frac{1}{2} \times 23.5 = 11.75 \, \text{cm} \)

Final Answer:
The value of \( \frac{1}{2} (DE + EF + DF) \) is \( 11.75 \, \text{cm} \).

---