ABCD एक चतुर्भुज है ।क्या AB+BC+CD+DA>AC+BD?
The correct Answer is:हाँ
Step by step video, text & image solution for ABCD एक चतुर्भुज है ।क्या AB+BC+CD+DA gt AC+BD? by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Topper's Solved these Questions
- BOOK - NCERT HINDICHAPTER - त्रिभुज और उसके गुणEXERCISE - प्रश्नावली 6.58videos
त्रिभुज और उसके गुण
- BOOK - NCERT HINDICHAPTER - त्रिभुज और उसके गुणEXERCISE - प्रश्नावली 6.32videos
त्रिभुज और उसके गुण
- BOOK - NCERT HINDICHAPTER - ठोस आकारों का चित्रण EXERCISE - इन्हें कीजिए2videos
ठोस आकारों का चित्रण
- BOOK - NCERT HINDICHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - प्रस्नावली 7.29videos
त्रिभुजों की सर्वांगसमता
Similar Questions
PQR एक त्रिभुज है जिसका P एक समकोण है । यदि PQ=10cm तथा PR=24cm तब QR ज्ञात कीजिए ।
03:57View Solutionनिम्नांकित आकृतियों में अज्ञात x का मान ज्ञात कीजिए।
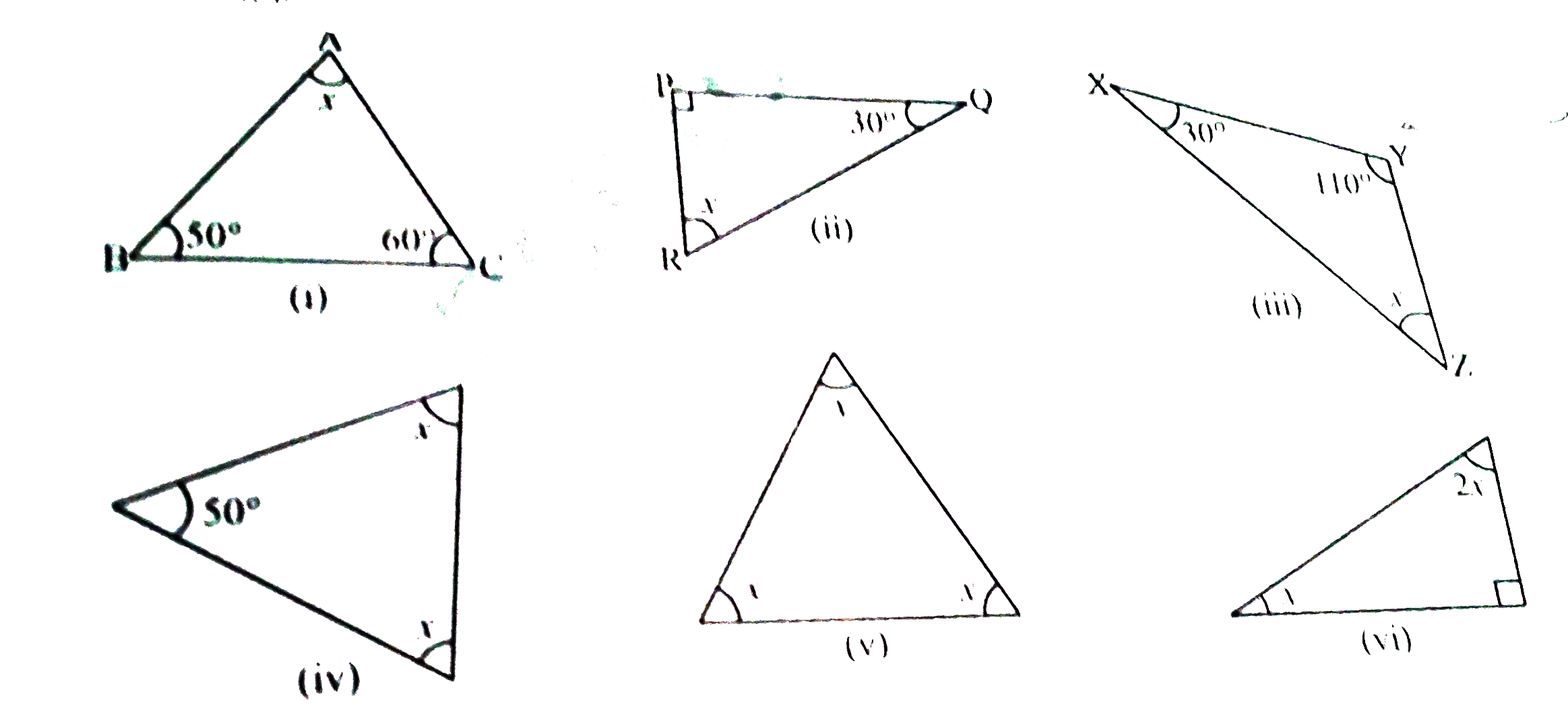 05:33View Solution
05:33View Solutionनिम्नलिखित सारणी को पूरा कीजिएः
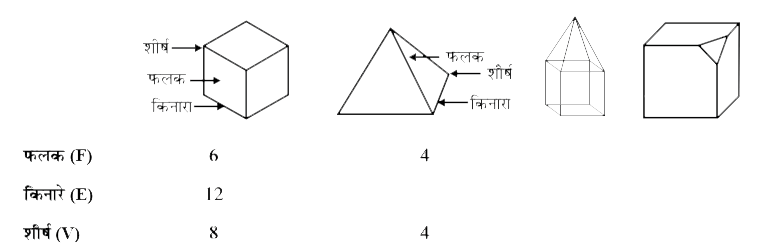 02:01View Solution
02:01View Solutionनिम्न में आप कौन से सर्वांगसम प्रतिबंधों का प्रयोग करेंगे?
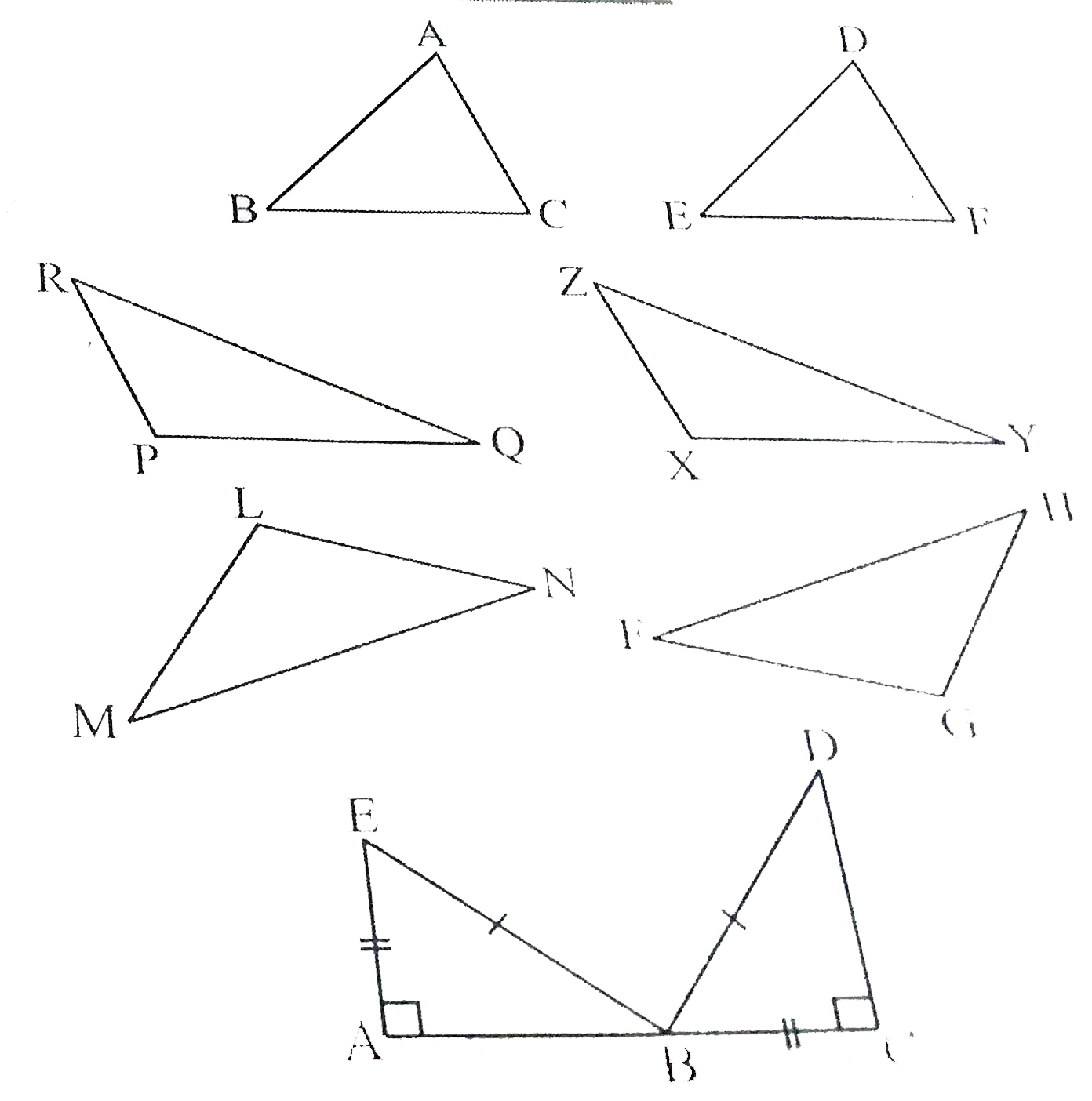 05:24View Solution
05:24View SolutionABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
03:36View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
04:43View SolutionShow that in a quadrilateral ABCD AB+BC+CD+DA>AC+BD
03:03View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)
 04:38View Solution
04:38View SolutionIn a quadrilateral ABCD, show that
(AB+BC+CD+DA)>(AC+BD).View SolutionIn a quadrilateral ABCD, show that (AB+BC+CD+DA)<2(BD+AC).
03:34View Solutionदिखाइये कि एक चतुर्भुज ABCD में AB+BC+CD+DA>AC+BD
03:16View Solutionयदि ABCD एक चतुर्भुर्ज है जिसके विकर्ण AC और BD,O पर परिच्छेद करते है तो सिद्ध कीजिए की :
(i)(AB+BC+CD+DA)>(AC+BD)
(ii) (AB+BC+CD+DA)<2(AC+BD)
 04:17View Solution
04:17View Solutionयदि ABCD एक चतुर्भुज हों, तो सिद्ध कीजिए कि-
(i) AB + BC + CD + DA > 2AC
(ii) AB + BC + CD + DA > AC + BD05:43View SolutionABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
05:02View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
03:02View SolutionShow that in a quadrilateral ABCD AB+BC+CD+DA>AC+BD
03:25View Solution

