आयतन V तथा घनत्व ρ का एक ठोस दो द्रव जिनके घनत्व ρ1 तथा ρ2 हैं, में तैर रहा है। यदि ρ1<ρ<ρ2, तब गोले के ऊपरी आयतन तथा निचले आयतन भाग का अनुपात होगा
ρ−ρ1ρ2−ρ
ρ2−ρρ−ρ1
ρ+ρ1ρ+ρ2
ρ+ρ2ρ+ρ1
The correct Answer is:B
माना ठोस गोले का कुल आयतन V है
V=V1+V2
चूँकि गोला तैरता है
इसलिए Vρg=V1ρ1g+V2ρ2g
(V1+V2)ρg=V1ρ1g+V2ρ2g
या V1(ρ−ρ1)g=V2(ρ2−ρ)g
या V1V2=ρ2−ρρ−ρ1
Topper's Solved these Questions
- BOOK - ARIHANT HINDICHAPTER - द्रवों के गुण EXERCISE - प्रश्नावली स्तर 2 (दृढ़कथन-कारण प्रकार)5videos
द्रवों के गुण
- BOOK - ARIHANT HINDICHAPTER - द्रव व ठोसों के गुणEXERCISE - प्रश्नावली (विगत वर्ष के प्रश्न)20videos
द्रव व ठोसों के गुण
- BOOK - ARIHANT HINDICHAPTER - द्रव्यमान केंद्रEXERCISE - प्रश्नवली (विगत वर्षों के प्रश्न)7videos
द्रव्यमान केंद्र
Similar Questions
वक्तव्य I जब नली की ऊँचाई द्रव की ऊँचाई से कम मापी जाती है तब द्रव बाहर नहीं निकलता है।
वक्तव्य II नली की ऊँचाई पर चन्द्रतल नीचे की ओर होता है।03:00View Solutionएक U आकार के तार एवं हल्के दर्पण के बीच बनी एक पतली द्रव की फिल्म 1.5×10−2 न्यूटन के भार को आधारित करती है( चित्र में देखने) दर्पण की लम्बाई 30 सेमी है ओर इसका भार नगण्य है। द्रव की फिल्म का पृष्ट तनाव है।
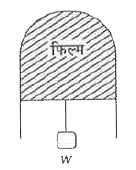 02:55View Solution
02:55View Solutionα कोण पर झुके नत समतल पर एक ठोस डिस्क नीचे की ओन लुढ़क रही है इसके द्रव्यमान केंद्र का त्वरण होगा
04:19View SolutionA solid sphere having volume V and density rho floats at the interface of two immiscible liquids of densityes rho_(1) and rho_(2) respectively. If rho_(1) lt rho lt rho_(2) , then the ratio of volume of the parts of the sphere in upper and lower liquid is
03:50View SolutionA solid uniform ball having volume V and density rho floats at the interface of two unmixible liquids as shown in Fig. 7(CF).7. The densities of the upper and lower liquids are rho_(1) and rho_(2) respectively, such that rho_(1) lt rho lt rho_(2) . What fractio9n of the volume of the ball will be in the lower liquid.
05:36View Solutionएक स्थिर आयतन वाले खुले टैंक का आधार वर्गाकार है। यदि अंत: पृष्ठ न्यूनतम हो, तब टैंक कि गहराई तथा लम्बाई का अनुपात ज्ञात कीजिए।
04:42View Solutionयदि a तथा b इकाई सदिश हैं तथा θ इनके बीच का कोण है। तब ∣∣ˆa+ˆb∣∣<1 यदि
View SolutionA uniform sphere of density ρ floats at the interface of two liquids of densities ρ1 and ρ2(>ρ1) The sphere has 23 rd of vertical diameter in denser liquid and remaining part in the other liquid.If aρ=bρ1+cρ2 then b+c-a=_______.
30:10View Solutionचित्रानुसार एक समरूप ठोस गेंद जिसका आयतन Vव घनत्व ρकी उभयनिष्ट सतह पर चित्रानुसार तैर रही है। उपरी द्रव और निचले द्रव के घनत्व क्रमशः ρ1 व ρ2 इस प्रकार है कि ρ1<ρ<ρ2 तो निचले द्रव में गेंद के आयतन का कितना भाग होगा
 03:59View Solution
03:59View SolutionA solid uniform ball of volume V floats on the interface of two immiscible liquids. The specific gravity of the upper liquid is rho_(1) and that of lower one is rho_(2) and the specific gravity of ball is rho(rho_(1) lt rho lt rho_(2)) . The fraction of the ball in the upper liquid Is
45:42View Solutionराजस्थान बोर्ड स्पेशल|पृषठीय क्षेत्रफल और आयतन#!#गोले तथा अर्ध गोले का पृषठीय क्षेत्रफल
03:20View SolutionA solid uniform ball having volume V and density rho floats at the interface of two unmixible liquids as shown in Fig. 7(CF).7. The densities of the upper and lower liquids are rho_(1) and rho_(2) respectively, such that rho_(1) lt rho lt rho_(2) . What fractio9n of the volume of the ball will be in the lower liquid.
04:08View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#गोले का पृष्ठीय क्षेत्रफल#!#गोले का आयतन#!#परीक्षा के लिए महत्वपूर्ण प्रश्न
05:04View SolutionA solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densites ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
01:33View SolutionA solid sphere of volume V and density ρ floats at the interface of two immiscible liquids of densities ρ1andρ2 respectively. If ρ1<ρ<ρ2, then the ration of volume of the parts of the sphere in upper and lower liquids is :
02:57View Solution

