ΔABC एक समद्विबाहु त्रिभुज है, जिसमें ∠B=90∘ है। दो समरूप त्रिभुज ACP तथा ABQ भुजाओं AC तथा AB पर खींचे गए हैं। ΔABQ तथा ΔACP के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
The correct Answer is:1:9
Topper's Solved these Questions
- त्रिभुज BOOK - BHARATI BHAWANCHAPTER - त्रिभुज EXERCISE - प्रश्नमाला 7A
14 Videos
- त्रिभुज BOOK - BHARATI BHAWANCHAPTER - त्रिभुज EXERCISE - प्रश्नमाला 7B
20 Videos
- त्रिकोणमितीय सर्वसमिकाएँ BOOK - BHARATI BHAWANCHAPTER - त्रिकोणमितीय सर्वसमिकाएँ EXERCISE - प्रश्नमाला 13C (बहुवैकल्पिक प्रश्न )
20 Videos
- दो चरों वाले रैखिक समीकरण - युग्म BOOK - BHARATI BHAWANCHAPTER - दो चरों वाले रैखिक समीकरण - युग्म EXERCISE - प्रश्नमाला 3F (बहुवैकल्पिक प्रश्न)
27 Videos
Similar Questions
किसी त्रिभुज ABC की भुजाओं AB और AC पर क्रमशः बिंदु D और E इस प्रकार हैं कि DE||BC है।
यदि AD = 2 cm, AB = 5cm तथा AE = 1.5cm हो, तो EC और AC ज्ञात कीजिए।
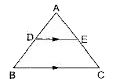
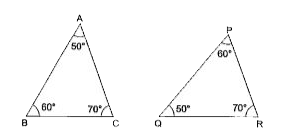
View Solutionबताइए कि निम्नांकित आकृति में दिए गए त्रिभुजों के युग्मों में से कौन-से युग्म समरूप - हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है, साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
View Solutionयदि sinA+sin2A=1 है, तो व्यंजक (cos2A+cos4A) का मान है
View Solutionयदि 2 x + 3y = 12 तथा 3 x - 2y = 5 है, तो
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View SolutionRevision |दो विशेष त्रिभुज : समबाहु तथा समद्विबाहु #!#एक त्रिभुज की दो भुजाओं की मापों का योग
View SolutionThe given figure shows a ΔABC in which AB =AC and BP =CQ .
Prove that :
(i) ΔABQ≅ΔACP.
(ii) ΔAPQ is isosceles.
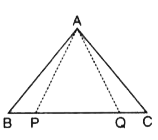
View SolutionABCDEF is a regular hexagon. What is the ratio of the area of triangle ACE and area of triangle AEF? ABCDEF एक सम षटभुज है। त्रिभुज ACE के क्षेत्रफल तथा त्रिभुज AEF के क्षेत्रफल का अनुपात क्या है?
View SolutionThe in-radius of a triangle is 6 cm, and the sum of the length of its sides is 50cm. The area of the triangle (in sq. cm) is एक त्रिभुज को अंतः त्रिज्या 6 सेमी है, तथा इसके भुजाओं के लंबाई का योग 50 सेमी है। त्रिभुज का क्षेत्रफल (वर्ग सेमी में) ज्ञात करें।
View Solutiontriangle ABC is similar to triangle DEF . The area of triangle ABC is 100 cm^2 and the area of triangle DEF is 49 cm^2 . If the altitude of triangle ABC =5cm, then the corresponding altitude of triangle DEF is: त्रिभुज ABC त्रिभुज DEF के समरूप है | त्रिभुज ABC का क्षेत्रफल 100 वर्ग सेमी है तथा त्रिभुज DEF का क्षेत्रफल 49 वर्ग सेमी है | यदि त्रिभुज ABC की ऊंचाई - 5 सेमी है, तो त्रिभुज DEF की संगत ऊंचाई ज्ञात करें |
View SolutionA circle is inscribed in triangle ABC , touching AB at P, BC at Q and AC at R. If AR=5 cm, RC= 6 cm and AB=12 cm, then perimeter of triangle ABC is: एक वृत्त किसी त्रिभुज ABC में समाहित है जो AB को P पर, BC को Q पर तथा AC को R पर स्पर्श करता है | यदि AR =5 सेमी और AB = 12 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
View SolutionThe sides AB and AC of a triangle ABC are extended to P and Q respectively. If the bisectors of angle PBC and angle QCB intersect at O, and angle A=92^@ , then angle BOC is equal to: एक त्रिभुज ABC की भुजाओं AB और AC को क्रमशः P तथा Q तक बढ़ाया जाता है | यदि angle PBC तथा angle QCB के समद्विभाजक एक दूसरे को O पर काटते हैं तथा angle A=92^@ है, तो angle BOC किसके बराबर है ?
View SolutionThe ratio of the areas of two triangles ABC and PQR is 3:5 and the ratio of their heights is 5:3. The ratio of the bases of triangle ABC to triangle PQR is : दो त्रिभुजों ABC और PQR के क्षेत्रफलों का अनुपात 3 : 5 है तथा उनकी ऊंचाई का अनुपात 5 : 3 है | त्रिभुज ABC और त्रिभुज PQR के आधारों के बीच अनुपात ज्ञात करें|
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 3 : 4 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 3 : 4 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान ज्ञात करें |
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 4:5 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 4:5 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान ज्ञात करें |
View SolutionThe ratio of the areas of two triangles ABC and PQR is 4:5 and the ratio of their heights is 5:3. The ratio of the bases of triangle ABC to that of triangle PQR is :
दो त्रिभुजों ABC और PQR के क्षेत्रफलों का अनुपात 4 : 5 है तथा उनकी ऊंचाई का अनुपात 5 : 3 है | त्रिभुज ABC तथा त्रिभुज PQR के आधारों के मध्य क्या अनुपात है ?
View Solution
